Таңдаманы практикада екі түрде өрнектейді: вариациалық қатар және интервалдық әдіс.
Таңдаманың мүшелерін вариация деп, ал олардың өсу бағытында жазылған қатарын вариациалық қатар деп атайды.
Таңдаманың сандық кездейсоқ шамаларын оқығанда 2 түрде кездеседі:
1. Дискретті кездейсоқ шамалар
2. Үздіксіз кездейсоқ шамалар
Дискретті кездейсоқ шамалар - бұл кездейсоқ шамалардың мәндерінің бір бірінен айырмашылығы қандай да соңғы шамада (шаруашылық саны, жанұя мүшелері).
Үзіліссіз кездейсоқ шамалар - бұл кездейсоқ шамалардың мәндерінің бір бірінен айырмашылығы қандай да кішкене шамада (бидайдың бір дәнінің салмағы).
Бас жиынға сәйкес кездейсоқ шамасы дискретті болған жағдайда дискретті статистикалық қатар салынады (кесте №1), ал кездейсоқ шамасы үздіксіз болған жағдайда жиіліктердің интервалдық статистикалық қатарлары пайдаланылады. Әр интервалда шекаралары жоғарғы, төменгі болып бөлінеді.
Математикалық статистикада таңдаманы оқығанда топтау әдісі кең таралған.
Топтау – статистикада берілгендерді ажыратқанда топтарға тек сапасы біртекті элементтер кіреді.
Вариация сілтеуі – вариациалық қатардың ең үлкен және ең кіші мәндерінің арасындағы айырмашылық.
R=xmax-xmin
Топтар саны – (бүтін сан)берілген жиынды жуықтап бөлшектейді, мына қатынастан анықталады.
k=int(1+3.322 lgn)
мұндағы n – таңдама көлемі,
int (integer – бүтін ) – бүтін бөлігі
Онда интервалдық қадам h (немесе топтау интервалының шамасы), жаңа пайда болған таңдамасы үшін есептеулерді мүмкіндігінше оңай жүргізуге болатындай таңдап алады. Көбіне h саны, көршілес терімдер айырымдары тұрақты болғандағы осы тұрақты санына тең.
h= 
Жинақталған жиілік – берілген терімнің жиілігінің алдындағы терімдердің жиіліктерінің қосыдысы.
Кесте №2
| Кездейсоқ шаманың әр түрлі мәндері xi | x1 | х2 | … | xi | … | xk |
| Жиіліктері mi | m1 | m2 | … | mi | … | mk |
| Жинақталған жиілік mжин | m1 | m1+m2 | … | m1+m2+…+mi | … |  mi
|
Интервалдық вариациялық қатар – жиіліктердің таңдаманың әр түрлі терімдеріне қатысты емес, ал θ тек барлық интервалға қатысты болғандағы кездейсоқ шамасының интервалдағы үлестірімі.
Интервалға оның ортасындағы мәні алынады.
6.4. Полигон, гистограмма, кумулята, огива.
Вариациялық қатарды - полигон, гистограмма, кумулята, огива графиктерінің маңызы зор.
Полигон үлестірімі тік бұрышты координаттар жүйесінде салынады. Абсцисса осіне Х кездейсоқ шамасының мәнін, ордината осінің бойынан - mi жиіліктерін, немесе (салыстырмалы жиіліктерін) 
жазады. Нүктелер (xi,mi) немесе (xi, ) кесінділермен қосылады. Шыққан сызықты полигон деп атайды, көбінесе дискреттік вариациалық қатарды бейнелеуге пайдаланылады.
Үлестірім гистограммасының полигоннан айырмашылығы ОХ осінде интервалдар салынады, ал ордината осіне жиіліктері немесе интервал жиіліктеріне пропорционал биіктіктерімен тік төртбұрыштар салынады. Егер тік төртбұрыштың жоғарғы қабырғаларының орталарын қоссақ онда үлестірім полигоны шығады. Кумулята (немесе қосындылардың қисығы) тік бұрышты координаталар жүйесінде салыстырмалы жиіліктері (немесе жиіліктері) бар вариациалық қатарды бейнелегенде шығады. Дискреттік кездейсоқ шамасына абсцисса осіне таңдаманың мәні салынады. Ал вертикаль осіне ұзындығы таңдаманың салыстырмалы жиілігіне (немесе жиілігіне) пропорционал болатын кесінділер қойылады.
Ординаталардың төбелерін қосқандағы шыққан қисық – кумулята деп аталады.
Огива кумулятаға ұқсас салынады, тек абсцисса осіне жинақталған жиіліктер, ординат осіне – таңдаманың мәні салынады.
Вариациялық қатардың сандық сипаттамаларын қарастырайық. Жай арифметикалық орта мына формуламен есептеледі.
Өлшенген арифметикалық орта мына формуламен есептеледі.
Орта шамалар вариациалық қатарларды бір санмен сипаттайды және вариациалық кездейсоқ шамаларды санамайды. Вариациалық кездейсоқ шамаларды өлшеу үшін – вариация сілтеуі, орташа сызықтық ауытқуы, орта квадраттық ауытқуы, вариация коэффициенті деген ұғымдар пайдаланылады.
Орта квадраттық ауытқу– таңдаманың абсолюттік мәндерінің ортадан ауытқуының арифметикалық ортасын ұсынады.
жай орташа сызықтық ауытқуы
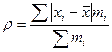- өлшенген орташа сызықтық ауытқуы
Таңдаманың дисперсиясы ( Орташа квадраттық ауытқуы) (кездейсоқ шаманың тұрақсыз өлшемі ретінде пайдаланылады)
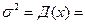
- өлшенген дисперсия
