Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.
Анықтама бойынша 
, мұндағы 
және 
- фокустар деп аталатын берілген нүктелер, 
-эллипстің бойындағы кез келген нүкте, 
-тұрақты шама.
Егер 
десек, онда 
, 
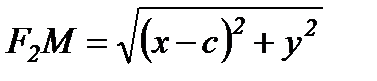. Енді осы мәндерді теңдеуіне қойып, түрлендіріп, эллипстің канондық теңдеуін аламыз:
(6.3)
мұндағы 
эллипстің үлкен жарты өсі, 
оның кіші жарты өсі болады. ны табу үшін эллипстің бойынан 
нүктесін аламыз. 
болғандықтан 
немесе 
болады. Пифагор теоремасы бойынша 
. Осыдан 
деп белгілейміз. 
қатынасын эллипстің эксцентриситеті деп атайды. 
болғандықтан 
. 
эллипстің директрисаларының теңдеуі. Ол эллипстің сыртында жатады.
51. Гиперболаның канондық теңдеуі. Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасының абсолюттік шамасы тұрақты 2а -ға тең болатын жазықтықтағы нүктелердің геометриялық орындарын гипербола деп атайды.
Гиперболаның канондық теңдеуі былай жазылады:
(6.4)
Мұндағы 
, 
- гиперболаның нақты жарты өсі, жорымал жарты өсі, гиперболаның эксцентриситеті, 
болғандықтан 
. Егер гиперболаның 
нүктесі шексіздікке ұмтылғанда нүктесінен түзуге дейінгі қашықтық нөлге ұмтылса, онда мұндай түзуді гиперболаның асиптотасы дейді. Гиперболаның асимптоталарының теңдеулері: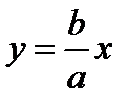 
және 
, мұндағы және гиперболаның жарты өстері. гиперболаның директрисаларының теңдеуі. Гиперболаның директрисалары оның төбелерінің арасында жатады
52. Параболаның канондық теңдеуі.. Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы тұрақты шама болатын жазықтықтағы нүктелердің геометриялық орындарын эллипс деп атайды.
Анықтама бойынша , мұндағы және - фокустар деп аталатын берілген нүктелер, -эллипстің бойындағы кез келген нүкте, -тұрақты шама.
Егер десек, онда , 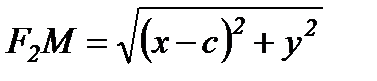. Енді осы мәндерді теңдеуіне қойып, түрлендіріп, эллипстің канондық теңдеуін аламыз:
(6.3)
мұндағы эллипстің үлкен жарты өсі, оның кіші жарты өсі болады. ны табу үшін эллипстің бойынан нүктесін аламыз. болғандықтан немесе болады. Пифагор теоремасы бойынша . Осыдан деп белгілейміз. қатынасын эллипстің эксцентриситеті деп атайды. болғандықтан . эллипстің директрисаларының теңдеуі. Ол эллипстің сыртында жатады.
53. Екінші ретті беттердің канондық теңдеулері. Екінші ретті беттер деп, координаталар жүйесінде екінші дәрежелі теңдеулермен берілетін беттерді айтады.
Екінші ретті беттердің қасиеттері техникада, құрылыс негіздерінің конструкцияларында сонымен бірге күн сәулесінің қуатын от қуатына айналдыру мақсатында қолданылады.
Мысалы, шағылыстыру айналары, түрлі прожекторлар параболоидтың қасиеттеріне, ал бір қуысты гиперболоидтың түзу сызықты жасаушылары болу қасиеттерін құрылыста қолданады. Ал сфералық айналарды қолданып, өмірдің түрлі қажетіне пайдаланады.
1. Сфера. Бекрілген нүктеден бірдей қашықтықта орналасқан
кеңістіктегі нүктелердің геометриялық орындарын сфералық немесе шар беті деп атайды.Егер сфераның центрі С(a,b,c) нүктесі және оның бетіндегі кез келген нүкте жылжымалы нүктесі M(x,y,z) болса, онда анықтама бойынша CM=R, R-сфераның радиусы.
Кеңістіктегі екі нүктенің арасындағы қашықтықтың формуласы бойынша
немесе - сфераның канондық теңдеуі.
2.Цилиндр. Цилиндр перпендикулчрлық қимасындағы сызықтың түріне қарай төрт түрге бөлінеді: дөңгелек, эллипстік, гиперболалық, және парболалық цилиндр болып, осыған сәйкес цилиндр тік бұрышты координаталар жүйесінде төрт түрлі теңдеумен анықталады:Бұл төрт теңдеу жазықтықта шеңберді, эллипсті, гиперболаны және паболаны кескіндейді, ал кеңістікте дөңгелек, эллипстік, гиперболалық және параболалық цилиндрлейді кескіндейді.Сонымен цилиндр (цилиндрлік бет) дегеніміз шеңбер, элллипс, гипербола, параболалардың бойымен олардың жазықтықтарына перпендикуляр болып өтетін түзу сызықтардың үздіксіз қозғалысынан шығатын екінші ретті беттер.Осы шеңбер, эллипс, гипербола, және парабола цилиндрлердің бағыттаушылары, ал цилиндрдің беттерінде жатқан түзулер олардың жасаушылары деп аталады.
3.Конус. Конус деп берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалысынан шығатын бетті айтады.
Конустың бағыттаушысы эллипс, ал жасаушы түзуі координаталардың бас нүктесінен өтсін. Сонда конустың теңдеуі:
болады.Мұндағы z=c конусты XOY жазықтығына параллель қиып өтетін жазықтық. Ал егер a=b болса, онда конустың перпендикулярлық қимасы шеңбер болады:
- айнымалы концстың теңдеуі. Төбесі координаталардың бас нүктесінде апликата осіне симметриялы екінші ретті конустық беттің теңдеуі.4.Айналу беттері. Егер кеңістікте бір сызық берілген осьті айналса, оның айналуынан бет п.б.Айналушы сызықтың формасына байланысты бет әр түрлі болады. Мысалы, егершеңберөзініңдиаметрібойыншаайналса, сфералық бет шығады, ал координаталарбасынанөтетінтүзу OZ осінайналса, дөңгелек конус п.б. Сызықтыңайналатыносінайналуосі, ал пайдаболғанбеттіайналубетідепатайды.Бізге YOZ жазықтығындажатқан L сызығытеңдеуіменберілсін. Осы сызықтың OY осінайналғандапайдаболғанбеттіңтеңдеуін табу үшінсолсызықтыңтеңдеудегі y – тіөзгертпей, z – тіөрнегіменалмастырукерек. Сонда айналубетініңтеңдеуімынандайболады:Басқаосьтердіайналғандапайдаболғанбеттердің де теңдеулеріосығанұқсастабылады. Яғни, егерберілгенсызық OZ осіненайналса, ондаайналубетініңтеңдеуіболады.
5. Айналу эллипсоиды.Үшосьті эллипсоид. YOZ жазықтығындатеңдеулеріменберілгенэллипсті OZ осіменайналдырғаннаншыққанбеттіайналу эллипсоид депатайды.6. Бірқуысты гиперболоид. Бізге YOZ жазықтығындаорналасқан гипербола теңдеуіменберілсін.
Осы гиперболаны OZ осіненайналдырсақбірқуысты гиперболоид депаталатынайналубетішығады. Оныңтеңдеуі
болады.
Осы айналугиперболоидындеформацияласақ, яғни
десек, ондамынатүргекеледі:
Осы теңдеуменанықталатынбеттібірқуысты гиперболоид депатайды. Айнымалыбірқуыстыгиперболоидтыңбірқуыстыгиперболоидтанайырмашылығыоның XOZ жазықтығына параллель жазықтықпенқимасы эллипс емесшеңберболады.
