 +
+ 
анықтауыштардың қосындысы түрінде жазайық. Сонда бірінші қосылғыш берілген анықтауыш болады да, екінші анықтауыш нолге тең.
6-қасиет.Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең:
 .
.
Теңдіктің дұрыстығын анықтауышты бірінші тік немесе үшінші жатық жол бойынша жіктеп тексеруге болады.
Осы қасиеттер көмегімен жоғары ретті анықтауыштар есептеуді көп жеңілдетуге болады. Анықтауышты қандай да бір жолында неғұрлым көп ноль болатындай етіп түрлендіріп, сол жол бойынша жіктеп анықтауыш реті төмендетіледі. Мысалы мынадай төртінші ретті
 анықтауышты есептейік.
анықтауышты есептейік.
Анықтауышты үшбұрышты түрге келтіреміз. Алдымен 5-қасиет бойынша анықтауыштың бірінші жолын 1-ге көбейтіп үшінші жолға, (-1)-ге көбейтіп төртінші жолға қосайық (есепте көрсетілген). Сонда анықтауыштың бірінші тік жолында  элементтен басқасы нолге айналады.
элементтен басқасы нолге айналады.
Енді осы қасиетті пайдаланып  элементінің астында тұрған сандарды нолге айналдырамыз. Соңында
элементінің астында тұрған сандарды нолге айналдырамыз. Соңында  элементінің астында тұрған сандарды нолге айналдырамыз. Анықтауыш үшбұрышты түрге келді. 6-қасиет бойынша анықтауыш мәнін диагональдік элементтерді көбейтіп табамыз.
элементінің астында тұрған сандарды нолге айналдырамыз. Анықтауыш үшбұрышты түрге келді. 6-қасиет бойынша анықтауыш мәнін диагональдік элементтерді көбейтіп табамыз.

 =
= 
 =
=

 =
=  =
=  .
.
16. Матрицаның рангі? Матрица рангі m x n өлшемді А матрицаның бірнеше жатық және тік жолдарын сызып тастап k өлшеміді, k  min (m,n), квадрат матрица алуға болады. Осы квадрат матрица анықтауышы берілген матрицаның k өлшемді миноры деп аталады.
min (m,n), квадрат матрица алуға болады. Осы квадрат матрица анықтауышы берілген матрицаның k өлшемді миноры деп аталады.  матрицаның k -өлшемді минорлар саны
матрицаның k -өлшемді минорлар саны 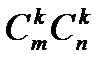 болады.
болады.
Анықтама. Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады: r=r(A)= rangA.
1.  матрицасының рангісі оның өлшемдерінің кішісінен артпайды: r(A)
матрицасының рангісі оның өлшемдерінің кішісінен артпайды: r(A)  min(m,n).
min(m,n).
2. Барлық элементтері ноль болғанда ғана (нолдік матрица) матрица рангісі ноль болады.
3. n–ретті квадрат матрица ерекше емес болғанда матрица рангісі n–ге тең болады.
Мысал.  матрицаның рангісін есептейік.
матрицаның рангісін есептейік.
Шешуі. Матрица өлшемі 3 х 4 болғандықтан, оның рангісі 3-тен артпайды, r(A)  min (3,4). Егер үшінші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі 3-ке тең болады. Үшінші ретті минорлар матрицаның бір тік жолын сызып тастағанда пайда болады:
min (3,4). Егер үшінші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі 3-ке тең болады. Үшінші ретті минорлар матрицаның бір тік жолын сызып тастағанда пайда болады:
 ,
,  ,
,  ,
, 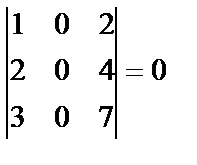 .
.
Үшінші ретті минорлардың бәрі нолге тең болғандықтан, ранг 3-ке тең бола алмайды. Енді екінші ретті минорлардың ішінен (олардың саны  ) ең болмағанда бір нолге тең емес минор тапсақ, матрица рангісі 2-ге тең болады. Екінші ретті минорлар матрицаның бір жатық, екі тік жолын сызып тастағанда пайда болады. Айталық бірінші жатық жол мен бірінші және екінші тік жолдарды сызып тастағанда пайда болатын мына минор:
) ең болмағанда бір нолге тең емес минор тапсақ, матрица рангісі 2-ге тең болады. Екінші ретті минорлар матрицаның бір жатық, екі тік жолын сызып тастағанда пайда болады. Айталық бірінші жатық жол мен бірінші және екінші тік жолдарды сызып тастағанда пайда болатын мына минор:  , сондықтан r(A)=2.
, сондықтан r(A)=2.
Матрица өлшемі артқан сайын оның рангісін барлық нолден өзге минорларды есептеу жолымен анықтау қиындайды. Матрица рангісін элементар түрлендірулер әдісімен табу ондай қиындықтардан құтқарады.
Теорема.Элементар түрлендірулер матрица рангісін өзгертпейді.
Дәлелдеуі. Матрицаға элементар түрлендірулер жүргізгенде оның анықтауышы не өзгермей сақталады, не нолге тең емес санға көбейтіледі. Яғни, оның реті өзгермейді деген сөз. Олай болса, нолден өзгеше минорлардың немесе матрица рангісінің реті де өзгермейді.
Осы теореманы ескеріп, элементар түрлендірулер жасап, берілген матрицаны барлық диагоналдік элементтері нолден өзгеше болатындай етіп сатылы түрге келтіреміз:
 ,
,
мұндағы r  п. Осы шарттың орындалуын матрицаны транстонерлеу арқылы қамтамасыз етуге болады. Сонда матрицаның r–ретті нолден өзге миноры
п. Осы шарттың орындалуын матрицаны транстонерлеу арқылы қамтамасыз етуге болады. Сонда матрицаның r–ретті нолден өзге миноры
 бар болады да, матрица рангісі r-ге тең болады, яғни r(A)=r.
бар болады да, матрица рангісі r-ге тең болады, яғни r(A)=r.
Матрицанің рангісін есептеу
 матрицасының рангісін есептейік.
матрицасының рангісін есептейік.
Шешуі. Элементар түрлендірулер көмегімен матрицаны сатылы түрге келтіреміз.





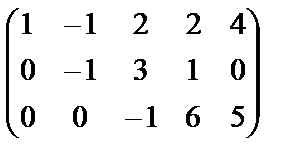 .Соңғы матрица сатылы түрге келді және онда нолге тең емес үшінші ретті минор бар екенін бірден көруге болады:
.Соңғы матрица сатылы түрге келді және онда нолге тең емес үшінші ретті минор бар екенін бірден көруге болады:
 . Сонымен матрица рангісі 3-ке тең, r(A)=3.
. Сонымен матрица рангісі 3-ке тең, r(A)=3.
17. Матрицаны түрлендіру? Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:
Қысқаша жазылуы: 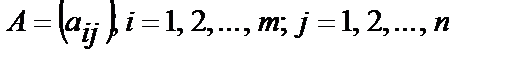
Матрица элементінің бірінші индексі жатық жол нөмірі, ал екінші индексі тік жол (бағана) нөмірін көрсетеді. Мысалы,  элементі екінші жатық жол мен үшінші тік жол қиылысында орналасқан.
элементі екінші жатық жол мен үшінші тік жол қиылысында орналасқан.
Бір ғана жатық жолдан құралған матрицаны жол-матрица, ал бір ғана тік жолдан құралған матрицаны бағана-матрица депатайды:  - жол-матрица;
- жол-матрица;
 - бағана матрица.
- бағана матрица.
Жол матрица мен бағана матрицаны кейде вектор деп те айтады.. Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады,
 .
.
Квадрат матрицаның 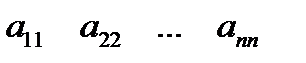 элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал
элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал  элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды. Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды. Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
 ,
, 
Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады,
 .
.
Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
 . Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
. Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
18.Кері матрица? Кері матрицаның анықтамасы
Кез келген  сан үшін мына
сан үшін мына 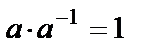 теңдігін қанағаттандыратындай кері сан табылады. Квадрат матрица үшін де осындай ұғым енгіземіз. Анықтама.А квадрат матрица үшін мына
теңдігін қанағаттандыратындай кері сан табылады. Квадрат матрица үшін де осындай ұғым енгіземіз. Анықтама.А квадрат матрица үшін мына  теңдікті қанағаттандыратын
теңдікті қанағаттандыратын  матрица А матрицаның кері матрицасы деп аталады. Кері матрицаны мына формуламен табады:
матрица А матрицаның кері матрицасы деп аталады. Кері матрицаны мына формуламен табады:
 , мұндағы
, мұндағы  -матрица анықтауышы, ал
-матрица анықтауышы, ал  -берілген матрицаның
-берілген матрицаның  элементтерінің алгебралық толықтауыштары, i=1,2,…,n; j=1,2,…,n.
элементтерінің алгебралық толықтауыштары, i=1,2,…,n; j=1,2,…,n.
Кез келген квадрат матрицаның кері матрицасы бола бермейді. Теорема (кері матрица болуының қажетті және жеткілікті шарты). Матрицаның кері матрицасы болуы үшін ол ерекше емес (  ) матрица болуы қажетті және жеткілікті.
) матрица болуы қажетті және жеткілікті.
Мысал.  матрицасының кері матрицасын табу керек. Шешуі. Алдымен анықтауышын есептейік.
матрицасының кері матрицасын табу керек. Шешуі. Алдымен анықтауышын есептейік.

 =
=  =
= 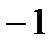 .
.
 , яғни кері матрица бар. Енді элементтердің алгебралық толықтауыштарын есептейік.
, яғни кері матрица бар. Енді элементтердің алгебралық толықтауыштарын есептейік.
 ,
,  ,
,
 ,
,  ,
,
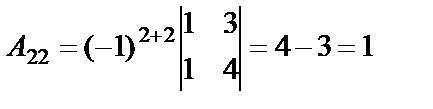 ,
, 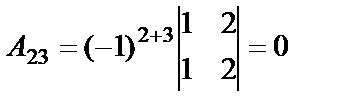 ,
,
 ,
, 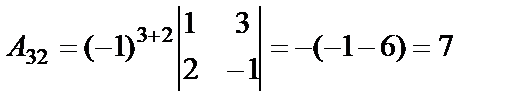 ,
,
 .
.
Табылған мәндерді формулаға қойып кері матрицаны табамыз.

 . Кері матрицаның дұрыс табылғандығын
. Кері матрицаның дұрыс табылғандығын  теңдігін тексеру арқылы көз жеткізуге болады:
теңдігін тексеру арқылы көз жеткізуге болады:
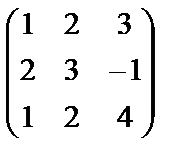


 .
.
Берілген матрицаға кері матрицаны элементар түрлендірулер әдісімен де табуға болады. Бұл әдіс матрицаға элементар түрлендірулер қолдануға сүйенеді. Матрицаның элементар түрлендірулері деп мынадай түрлендірулерді айтамыз:
1) Матрицаны транспонерлеу;
2) Жолдардың орнын алмастыру;
3) Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейту;
4) Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейтіп басқа жолдың сәйкес элементтеріне қосу;
5) Барлық элементі ноль болатын жолды алып тастау.
Енді кері матрица табу ережесіне көшейік: Берілген 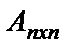 матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда
матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда  өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында
өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында  кері матрица пайда болады.
кері матрица пайда болады.
Мысалы, жоғарыдағы қарастырылған  матрицаның кері матрицасын осы әдіспен тауып көрейік. Берілген матрицаның оң жағына бірлік матрица жазып, элементар түрлендірулер жүргіземіз.
матрицаның кері матрицасын осы әдіспен тауып көрейік. Берілген матрицаның оң жағына бірлік матрица жазып, элементар түрлендірулер жүргіземіз.







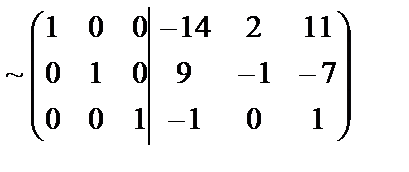 .
.
Соңында бірлік матрицаның орнында пайда болған матрица кері матрица болады:  . Ерекше емес матрицалар үшін мынадай қасиеттер дұрыс болады:
. Ерекше емес матрицалар үшін мынадай қасиеттер дұрыс болады:
1)  , 2)
, 2) 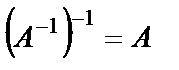 ,
,
3)  , 4)
, 4)  .
.
Соңғы  ,...,
,...,  теңдеулеріндегі
теңдеулеріндегі  ,...,
,...,  сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады.
сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады.
Жүйенің рангісі жүйедегі белгісіздер санынан кем болса, онда жүйе анықталмаған болатыны жоғарыда айтылған. Айталық (6) жүйе үйлесімді және r<n болсын. Егер  коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда
коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда  айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды. Еркін айнымалылары нолге тең болған кездегі шешім базистік шешім деп аталады. Базистік шешімдер саны
айнымалыларды базистік (негізгі) айнымалылар деп, ал басқа n-r айнымалыларды еркін (негізгі емес) айнымалылар деп атайды. Еркін айнымалылары нолге тең болған кездегі шешім базистік шешім деп аталады. Базистік шешімдер саны  -ден артпайды.
-ден артпайды.
1-мысал.  Шешуі. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
Шешуі. Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
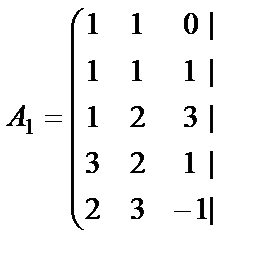














 .
.
Соңғы матрицаға сәйкес келетін жүйе жазайық: 
Сонымен жүйенің шешімі табылды:
19. Жүйенің шешімі дегеніміз не?
Негізгі ұғымдар мен анықтамалар. n белгісізді m теңдеуден тұратын жүйе деп мынадай жүйені айтады:
 (1)
(1)
мұндағы  (i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал
(i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал  (i=1,2,…,m) - бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:
(i=1,2,…,m) - бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:  (i=1,2,…,m)
(i=1,2,…,m)
жүйенің бос мүшелерінің бәрі нолге тең болса,  (i=1,2,…,m) жүйе біртекті жүйе деп аталады. Жүйенің әрбір теңдеуін тепе-теңдікке айналдыратын
(i=1,2,…,m) жүйе біртекті жүйе деп аталады. Жүйенің әрбір теңдеуін тепе-теңдікке айналдыратын 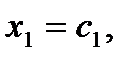


сандар тізбегі теңдеулер жүйесінің шешімі деп аталады. Осы шартты қанағаттандыратын барлық  шешімдер шешімдер жиынын құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді.
шешімдер шешімдер жиынын құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді.
(1) жүйенің ең болмағанда бір шешімі болса жүйе үйлесімді, ал шешімі болмаса үйлесімсіз деп аталады. Үйлесімді жүйенің бір ғана шешімі болса, жүйе анықталған, ал шешімі бірден көп болса анықталмаған деп аталады. Енді (1) жүйеге мынадай белгілеулер енгізейік:
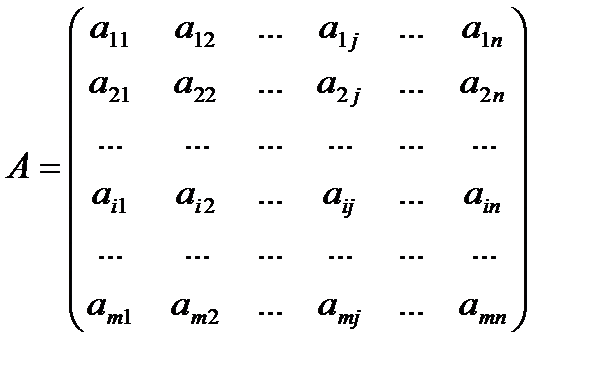 ,
,  ,
, 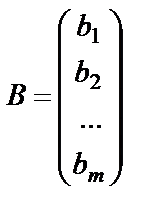
А - жүйе коэффициенттерінен құрылған матрица немесе жүйе матрицасы, Х - жүйенің бос мүшелерінен құрылған бағана матрица, В - жүйенің бос мүшелерінен құрылған бағана матрица. Осы белгілеулерді қолданып (1) жүйені былайша жазуға болады: АХ=В (3). (3) теңдеу (1) жүйенің матрицалық жазылуы болып табылады. Егер жүйе матрицасына бос мүшелер матрицасын жалғап жазсақ,

 , жүйенің кеңейтілген матрицасын аламыз.
, жүйенің кеңейтілген матрицасын аламыз.
Кронеккер-Капелли теоремасы. Егер сызықты теңдеулер жүйесінің негізгі матрицасы мен кеңейтілген матрицасының ранглері тең болса, онда жүйе үйлесімді болады.
Теорема бойынша жүйе үйлесімді болуы үшін  болуы керек. Бұл кезде rжүйе рангісі деп аталады.
болуы керек. Бұл кезде rжүйе рангісі деп аталады.
Үйлесімді жүйенің рангісі жүйедегі белгісіздер санына тең болса (r=n), онда жүйе анықталған болады, ал егер жүйенің рангісі жүйедегі белгісіздер санынан кем болса (r<n), онда жүйе анықталмаған болады. Мысалы, мынадай жүйе қарастырайық:
 Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:
Жүйенің кеңейтілген матрицасын жазып, элементар түрлендірулер жасайық:


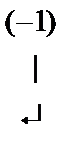


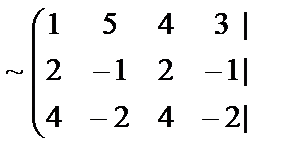


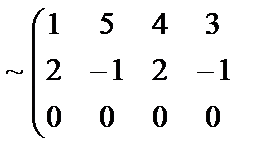




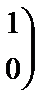
Жүйе матрицасы мен кеңейтілген матрицаның екінші ретті нолге тең емес минорлары бар екенін көру қиын емес және  . Кронеккер-Капелли теоремасы бойынша жүйе үйлесімді. Жүйе рангісі r=2, ал белгісіздер саны n=4, r<n болғандықтан жүйе анықталмаған, яғни шексіз көп шешімі бар.
. Кронеккер-Капелли теоремасы бойынша жүйе үйлесімді. Жүйе рангісі r=2, ал белгісіздер саны n=4, r<n болғандықтан жүйе анықталмаған, яғни шексіз көп шешімі бар.
20. Қандай жүйе үйлесімді деп аталады? Негізгі ұғымдар мен анықтамалар. n белгісізді m теңдеуден тұратын жүйе деп мынадай жүйені айтады:  (1)мұндағы
(1)мұндағы  (i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал
(i=1,2,…,m, j=1,2,…,n) - теңдеу коэффициенттері деп, ал  (i=1,2,…,m) - бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:
(i=1,2,…,m) - бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:  (i=1,2,…,m)
(i=1,2,…,m)






