(4.6)
7. Екі түзудің арасындағы бұрыш.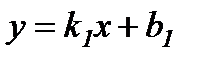 
және 
түзулерінің арасындағы бұрыштың формуласы:
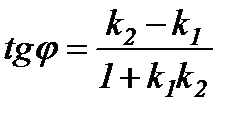(4.7)
Осыдан егер түзулер параллель болса, онда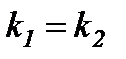 
, ал түзулер перпендикуляр болса, онда 
болады. Түзулер 
және 
теңдеулерімен берілсе, онда 
, 
болғандықтан түзулердің арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:
(4.8)
Осыдан егер түзулер параллель болса, онда 
, ал перпендикуляр болса, онда 
болады.
8. Нүктеден түзуге дейінгі қашықтық. 
нүктесінен 
түзуіне дейінгі қашықтықтың формуласы:
(4.9)
2-мысал. 
нұктесінен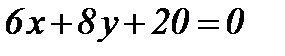 
тұзуіне дейінгі қашықтықты табу керек.
41. Түзулердің арасындағы бұрыш. 5. Екі түзудің арасындағы бұрыш. Екі түзу канондық теңдеулерімен берілсін:
және 
Екі түзудің арасындағы бұрыш, сол түзулердің бағыттаушы векторларының арасындағы бұрышқа тең (
, 
):
(5.10)
Егер түзулер өзара параллель болса, онда 
|| 
болады. Түзулердің параллелдік шарты:
, егер түзулер өзара перпендикуляр болса, онда 
болады. Түзулердің перпендикулярлық шарты: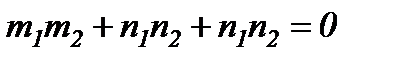 
болады.
Осыдан 
немесе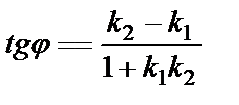 
(7)
(7) формула берілген екі түзу арасындағы бұрышты анықтайды. Ал екінші бұрыш 
тең болады.
|
|
|
|
|
|
|
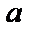
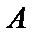
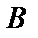
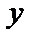
| 8-сурет |
Егер екі түзу параллель болса, онда 
=0 болады да tg =0. Бұл жағдайда (7) формула мынадай түрге келеді: k 2 – k 1 = 0. Осыдан екі түзудің параллелдік шарты шығады: k 2 = k 1 , (8) яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше. Егер екі түзу перпендикуляр болса, онда 
болады да, 
, 
. Осыдан екі түзудің перпендикулярлық шарты шығады: k 2 = 
,
яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше.
43. Нүктеден түзуге дейінгі қашықтық. 6. Нүктеден түзуге дейінгі қашықтық
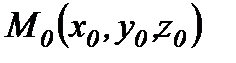нүктесінен 
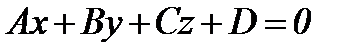түзуіне дейінгі қашықтықтың формуласы:
44. Жазықтықтың әртүрлі теңдеулері. 1. Берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі
Жазықтықта 
нүктесі және оған перпендикуляр 
векторы берілсін. Сонда берілген нүкте арқылы, берілген векторға перпендикуляр өтетін жазықтықтың теңдеуі төменгідей болады:
(5.1)
2. Жазықтықтың жалпы теңдеуі
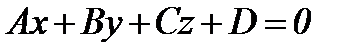(5.2)
Егер D=0 болса, онда жазықтық бас нүкте арқылы өтеді; егер C=0 онда, жазықтық Oz өсіне параллель өтеді; егер C=D=0 болса, онда жазықтық бас нүкте арқылы Oz өсіне параллель өтеді; егер A=B=D=0 болса, онда z=0 болады. Бұл Oxy жазықтығы.
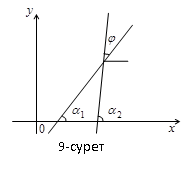
42. Екі түзудің параллельдік және перпендикулярлық шарттары. Екі түзу берілсін: y=k 1 x+b 1, y=k 2 x+b 2. Мұндағы  ,  . Екі түзу арасындағы бұрышты табу керек (9-сурет). Суреттен көрініп тұрғандай  .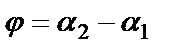
|
3. Үш нүкте арқылы өтетін жазықтықтың теңдеуі. , 
және 
нүктелері арқылы өтетін жазықтықтың теңдеуі:
(5.3)
4. Жазықтықтың кесінділік теңдеуі
Жазықтықта берілген 2 нукте арқылы өткен түзу теңдеуі
|
|
|
|
|
|
|
|
|
|
|
|
|
|
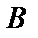
| 7-сурет |
Берілген 2 нүкте арқылы өткен түзу теңдеуі. 
және 
нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:
y =k(x – x1)+ y1.
АВ түзуі нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y2 =k(x2 – x1)+ y1. Осы теңдіктен белгісіз k табылады, 
. Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз:
Түзудің жалпы және кесінділік теңдеуі
Түзудің “кесіндідегі” теңдеуі. Түзу Ох осінен а-ға тең, Оу осінен b-ға тең кесінді қиып өтсін (8-сурет). Түзу А(а;0) және В(0;b) нүктелері арқылы өтеді деп, (5) теңдеуді қолданайық. Сонда түзу теңдеуі мынадай түрде жазылады:
Енді ықшамдасақ, түзудің “кесіндідегі” теңдеуін аламыз: 
45. Екі жазықтықтың арасындағы бұрыш. 5. Екі жазықтықтың арасындағы бұрыш. Жазықтықтар 
және 
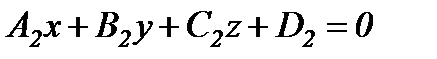теңдеулерімен берілсе, онда 
, 
болғандықтан жазықтықтардың арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:
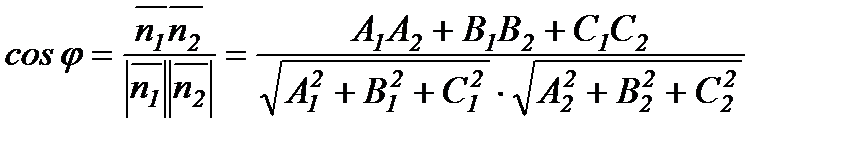(5.5)
Осыдан егер жазықтықтар параллель болса, онда 
, ал перпендикуляр болса, онда 
болады.
46. Екі жазықтықтың параллельдік және перпендикулярлық шарттары.
Егер екі түзу параллель болса, онда =0 болады да tg =0. Бұл жағдайда (7) формула мынадай түрге келеді: k2 – k1 = 0. Осыдан екі түзудің параллелдік шарты шығады: k2 = k1 , (8) яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше. Егер екі түзу перпендикуляр болса, онда болады да, , . Осыдан екі түзудің перпендикулярлық шарты шығады: k2 = ,
яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше.
47. Нүктеден жазықтыққа дейінгі қашықтық.
Нүктеден түзуге дейінгі қашықтық. нүктесінен түзуіне дейінгі қашықтықтың формуласы:
(4.9)
2-мысал. нұктесінен 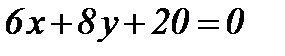тұзуіне дейінгі қашықтықты табу керек.
48. Кеңістіктегі түзудің әртүрлі теңдеулері. Екі нуктенін ара қашықтығы
Жазықтықта және екі нүкте берілсін. Осы екі нүкте арақашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:
.
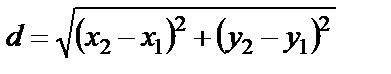Түзудің жалпы теңдеуі
(4.1) теңдеуінде жақшаларды ашып,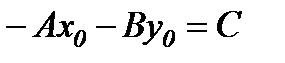 
деп белгілесек, түзудің жалпы теңдеуі шығады
(4.2)
Егер А=0 болса, онда түзу Ох өсіне параллель өтеді; егер В=0 болса, онда түзу Оу өсіне параллель өтеді; егер С=0 болса, онда түзу жүйенің бас нүктесі арқылы өтеді.
Нүктеден түзуге дейінгі қашықтық. нүктесінен түзуіне дейінгі қашықтықтың формуласы:
(4.9)
2-мысал. нұктесінен 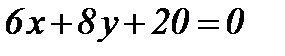тұзуіне дейінгі қашықтықты табу керек.
Екі нүкте арқылы өтетін түзудің теңдеуі. Түзу және 
нүктелерінен өтсін. Түзудің бойынан кез келген 
нүктесін аламыз. Сонда бұл түзудің теңдеуі төмендегідей болады:
Екі түзудің арасындағы бұрыш. 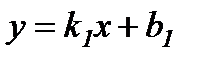және түзулерінің арасындағы бұрыштың формуласы:
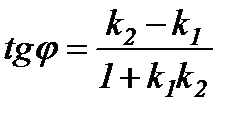(4.7)
Осыдан егер түзулер параллель болса, онда 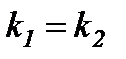, ал түзулер перпендикуляр болса, онда болады. Түзулер және теңдеулерімен берілсе, онда , болғандықтан түзулердің арасындағы бұрыш осы екі нормальдің арасындағы бұрышқа тең:
(4.8)
Осыдан егер түзулер параллель болса, онда , ал перпендикуляр болса, онда болады.
49. Түзу мен жазықтықтың өзара орналасуы. Кеңістіктегі түзудің орны осы түзуде жататын бір 
нүктесі және осы түзуге параллель 
векторы арқылы анықталады. Кеңістіктегі осы түзудің теңдеуін қорытып шығарамыз. Түзудің теңдеуін құру үшін түзудің бойынан кез келген ағымдағы координаталарымен 
нүктесін аламыз да М0 және М нүктелерін координаталарымен саламыз да М0 және М нүктелерін координаталар басымен қосамыз және координаталарын табамыз:
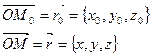
болатыны суерттен көрініп тұр. Егер М нүктесі түзу бойынд жататын болса, онда 
және векторлары коллинеарт болады. Ендеше, бұл векторлар 
коллинеарлық шартын қанағаттандырады, мұндағы t - параметр.
Векторлардың коллинеарлық шартын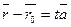 
(1) түрінде жазамыз, бұл түзудің векторлық теңдеуі.
(1) түзудің векторлық теңдеуі, 
нүктесі мен бағыттаушы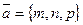 
векторының координаталары берілсін.
(1) теңдеудің сол жағын векторлық түрде жазамыз
және бағыттаушы вектор
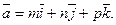
Сонда (1) теңдеу мына түрге келеді:
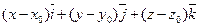
Теңдіктің оң және сол бөліктеріндегі бірлік векторлардың сәйкес коэффициенттерін теңестіріп, түзудің параметрлік теңдеуін аламыз.
немесе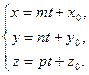 
(2)
(2)- параметрлік теңдеу.
(2) теңдеудегі t параметрінен құтылып, түзудің канондық теңдеуін аламыз:
(3)
Мысал.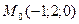 
нүктесінен өтетін және 
векторына параллель түзудің канондық және параметрлік теңдеуін құру керек.
(3): 
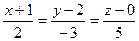
(2): 
Кеңістіктегі түзудің жалпы теңдеуі. Кеңістікте түзу екі жазықтықтың қиылысуымен анықталатын болғандықтан, онда оның кеңістіктегі жалпы теңдеуі
(4)
жүйесі түрінде өрнектеледі, мұндағы бірінші және екіні теңдеулер сәйкес жазықтықтар теңдеулері.
