Диагональ матрица


Егер квадрат матрицаның бас диагональдан тыс элементтері нөлге тең болса, онда ондай матрицаны диагональ матрица дейді.
6.Бірлік матрица? Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
 . Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
. Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
7.Үшбұрышты матрица дегеніміз не? Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
 ,
,  8.Матрицаларға қолданылатын амалдар? Матрицаны санға көбейту. 1. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
8.Матрицаларға қолданылатын амалдар? Матрицаны санға көбейту. 1. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
Мысалы, 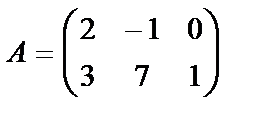 матрицасын
матрицасын  санына көбейтейік:.
санына көбейтейік:.
Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
2.Матрицаларды қосу және алу. 2. Матрицаларды қосу және алу. Өлшемдері бірдей матрицаларды ғана қосуға болады. А және В матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз: 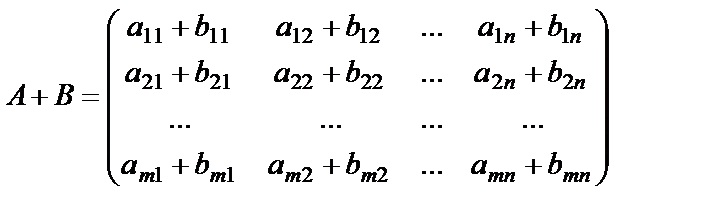 .
.
А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:A – B = A+(-1)B немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық:
3.Матрицаларды көбейту. 3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі m x k болатын А матрицасы мен өлшемі k x n болатын В матриасы берілсін:
Осы екі матрицаны көбейткенде өлшемі m x n болатын көбейтінді С матрица аламыз:

С матрицасының  элементі А матрицаның
элементі А матрицаның  –жатық жол элементтерін В матрицаның
–жатық жол элементтерін В матрицаның  –тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:
–тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:  ,
,  . (1) Мысалы,
. (1) Мысалы,  матрицасы мен
матрицасы мен  матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
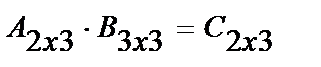 , яғни,
, яғни, 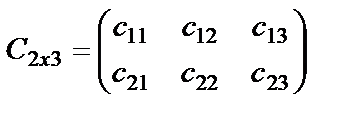 . k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады:
. k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады:  ,
,  .
.  элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда
элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда  , яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:
, яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:
C= 
 =
= 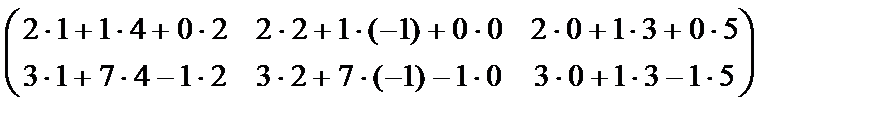 = =
= = 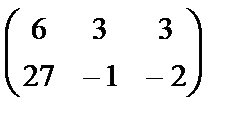 .
.
Қосу және көбейту амалдарының мынадай қасиеттері бар:
| 1) A+B=B+A | 5) (A+B)C=AC+BC |
| 2) (A+B)+C=A+(B+C) | 6) 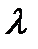 (AB)=( (AB)=(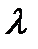 A)B=A( A)B=A(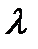 B) B)
|
3) 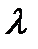 (A+B)= (A+B)= 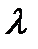 A+ A+ 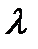 B B
| 7) A(BC)=(AB)C |
| 4) A(B+C)=AB+AC |
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.
8) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА көбейтіндісі болмауы мүмкін. Мысалы,  көбейтіндісі бар, бірақ
көбейтіндісі бар, бірақ 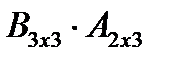 көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;
көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;
екіншіден, АВ және ВА көбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін. Мысалы,  және
және  көбейтінділер бар, бірақ өлшемдері әртүрлі:
көбейтінділер бар, бірақ өлшемдері әртүрлі:  ,
, 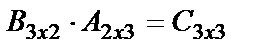 ; үшіншіден, АВ және ВА көбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ
; үшіншіден, АВ және ВА көбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ 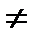 BA.
BA.
Мыс:  мен
мен  матрицалары берілген. АВ және ВА көбейтінділерін табау керек. Шешуі. Берілген матрицалар өлшемдері 2 х 2 квадрат матрицалар, оларды көбейтуге болады:
матрицалары берілген. АВ және ВА көбейтінділерін табау керек. Шешуі. Берілген матрицалар өлшемдері 2 х 2 квадрат матрицалар, оларды көбейтуге болады:
 .
.
 .
.
Көріп отырғанымыздай АВ 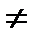 BA.
BA.
9) А -квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А.
9.Матрицаларды қосу және матрицаны санға көбейту амалдарының қасиеттері? Өлшемдері бірдей матрицаларды ғана қосуға болады. А және В матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:
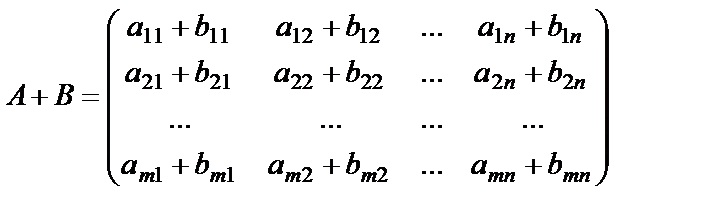
Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
Мысалы, 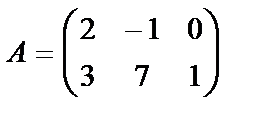 матрицасын
матрицасын  санына көбейтейік:Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
санына көбейтейік:Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
1. Матрицалардың санға көбейтіндісі.
Әрбір матрицаны санға көбейтуге болады. Ол үшін матрицаның әр элементін сол санға көбейту керек.
Мысалы 
10. Матрицаларды көбейту амалының қасиеттері? Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі mxk болатын А матрицасы мен өлшемі kxn болатын В матриасы берілсін: Осы екі матрицаны көбейткенде өлшемі mxn болатын көбейтінді С матрица аламыз:

С матрицасының  элементі А матрицаның
элементі А матрицаның  –жатық жол элементтерін В матрицаның
–жатық жол элементтерін В матрицаның  –тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:
–тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:  ,
,  . (1) Мысалы,
. (1) Мысалы,  матрицасы мен
матрицасы мен  матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
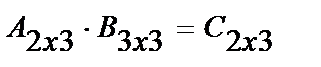 , яғни,
, яғни, 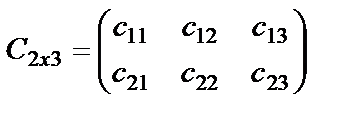 . k=3 болғандықтан(1) формуланы қолданғанда үш қосылғыш болады:
. k=3 болғандықтан(1) формуланы қолданғанда үш қосылғыш болады:  ,
,  .
.  элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда
элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда  ,яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:
,яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:
C= 
 =
= 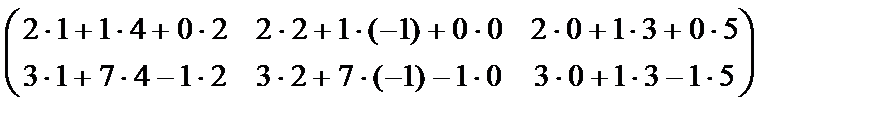 = =
= = 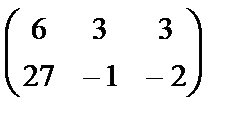 .
.
Қосу және көбейту амалдарының мынадай қасиеттері бар:
| 1) A+B=B+A | 5) (A+B)C=AC+BC |
| 2) (A+B)+C=A+(B+C) | 6) 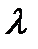 (AB)=( (AB)=(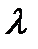 A)B=A( A)B=A(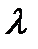 B) B)
|
3) 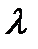 (A+B)= (A+B)= 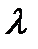 A+ A+ 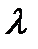 B B
| 7) A(BC)=(AB)C |
| 4) A(B+C)=AB+AC | |
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.
8 ) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА көбейтіндісі болмауы мүмкін. Мысалы,  көбейтіндісі бар, бірақ
көбейтіндісі бар, бірақ 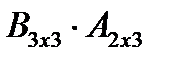 көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;
көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;
екіншіден, АВ және ВАкөбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін. Мысалы,  және
және  көбейтінділер бар, бірақ өлшемдері әртүрлі:
көбейтінділер бар, бірақ өлшемдері әртүрлі:  ,
, 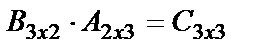 ; үшіншіден, АВ және ВАкөбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ
; үшіншіден, АВ және ВАкөбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ 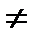 BA.
BA.
Мысал.  мен
мен  матрицалары берілген. АВ және ВАкөбейтінділерін табау керек. Шешуі. Берілген матрицалар өлшемдері 2х2 квадрат матрицалар, оларды көбейтуге болады:
матрицалары берілген. АВ және ВАкөбейтінділерін табау керек. Шешуі. Берілген матрицалар өлшемдері 2х2 квадрат матрицалар, оларды көбейтуге болады:
 .
.
 .
.
Көріп отырғанымыздай АВ 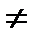 BA.
BA.
9 ) А-квадрат матрица болса, онда мына теңдік орындалады: АЕ = ЕА = А.
11. Екінші ретті анақтауыштың анықтамасы және есептелінілуі? Екінші ретті матрицаның  анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады:
анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады: 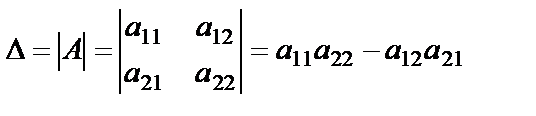
12. Үшінші ретті анақтауыштың анықтамасы және есептелінілуі. Үшінші ретті матрицаға  үшінші ретті анықтауыш сәйкес келеді:
үшінші ретті анықтауыш сәйкес келеді:

7. ajjэлементінің миноры дегеніміз не?
n-ретті квадрат матрицаның i–жатық жолы мен j–тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауықты  элементінің миноры деп атайды және
элементінің миноры деп атайды және  деп белгілейді.
деп белгілейді.
Үшінші ретті марицаның  элементінің миноры мынадай екінші ретті анықтауыш болады:
элементінің миноры мынадай екінші ретті анықтауыш болады:  .
.
 элементінің алгебралық толықтауышы деп мынадай санды айтады:
элементінің алгебралық толықтауышы деп мынадай санды айтады: 
3-ші ретті мат-ның  элементінің алгебралық толықтауышы мына сан:
элементінің алгебралық толықтауышы мына сан: 
Мысалы,  матрицасының бірінші жатық жолдағы элементтерінің миноры мен алгебралық толықтауыштарын есептейік:
матрицасының бірінші жатық жолдағы элементтерінің миноры мен алгебралық толықтауыштарын есептейік:
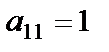 ,
,  ,
,  ,
,
 ,
, 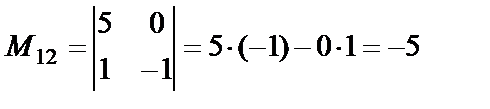
 ,
,
 ,
,  ,
,  .
.
Үшінші ретті анықтауыштың қасиеттері. 1. Анықтауштың жатық жолдарын оның сәйкес тік жолдарымен орын алмастырғаннан ол анықтауыштың сан мәні өзгермейді. Анықтауыштың жатық жолдары мен тік жолдарының орын алмастыру амалы оны транспозициялау деп аталады. 2. Егер анықтауыштың қандай болса да бір жатық жолының барлық элементтері нөлге тең болса, онда анықтауышнөлге тең болады. 3. Егер анықтауыштың екі жатық жолын бірі мен бірін орныдарынан алмастырсақ, онда анықтауыш таңбасы қарама-қарсы таңбаға ауады. 4. Егер анықтауыштың кез келген екі жатық жолы өзара тең болса, онда ол нөлге тең болады. 5. Егер анықтауыштың қандай болса да бір жатық жолының барлық элементтерін бір ғана  санына көбейтсек, онда анықтауыштың өзі осы γ санына көбетіледі. 6. Егер анықтауыштың екі жатық жолының элементтері пропорционал болса, онда мұндай анықтауыш нөлге тең болады. Егер анықтауыштың і-ші жатық жолының элементтері екі қосылғыш арқылы берілген болса, яғни
санына көбейтсек, онда анықтауыштың өзі осы γ санына көбетіледі. 6. Егер анықтауыштың екі жатық жолының элементтері пропорционал болса, онда мұндай анықтауыш нөлге тең болады. Егер анықтауыштың і-ші жатық жолының элементтері екі қосылғыш арқылы берілген болса, яғни  іj =
іj =  іj +
іj +  , ij=1,2,3 онда анықтауыш екі анықтауыштың қосындысына тең болады. Егер анықтауыштың қандай болса да бір жатық жолының элементтерін бір ғана
, ij=1,2,3 онда анықтауыш екі анықтауыштың қосындысына тең болады. Егер анықтауыштың қандай болса да бір жатық жолының элементтерін бір ғана  санына көбейтіп, басқа бір жатық жолының сәйкес элементтеріне қоссақ, онда бұдан анықтауыш шамасы өзгермейді.
санына көбейтіп, басқа бір жатық жолының сәйкес элементтеріне қоссақ, онда бұдан анықтауыш шамасы өзгермейді.
13.  Элементінің миноры дегеніміз не?
Элементінің миноры дегеніміз не?  квадрат матрицасының
квадрат матрицасының  элементінің миноры деп, осы элемент орналасқан жол мен бағанды сызып тастағаннан шығатын 3-ші ретті анықтауышты айтады және оны
элементінің миноры деп, осы элемент орналасқан жол мен бағанды сызып тастағаннан шығатын 3-ші ретті анықтауышты айтады және оны  деп белгілейді. Анықтама.n-ретті квадрат матрицаның i–жатық жолы мен j–тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауықты
деп белгілейді. Анықтама.n-ретті квадрат матрицаның i–жатық жолы мен j–тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауықты  элементінің миноры деп атайды және
элементінің миноры деп атайды және  деп белгілейді.
деп белгілейді.
Үшінші ретті марицаның  элементінің миноры мынадай екінші ретті анықтауыш болады:
элементінің миноры мынадай екінші ретті анықтауыш болады:  .
.
14.  Элементінің алгебралық толықтауышы дегеніміз не?
Элементінің алгебралық толықтауышы дегеніміз не?  элементінің алгебралық толықтауышы деп мынадай санды айтады:
элементінің алгебралық толықтауышы деп мынадай санды айтады: 
3-ші ретті мат-ның  элементінің алгебралық толықтауышы мына сан:
элементінің алгебралық толықтауышы мына сан: 
Мысалы,  матрицасының бірінші жатық жолдағы элементтерінің миноры мен алгебралық толықтауыштарын есептейік:
матрицасының бірінші жатық жолдағы элементтерінің миноры мен алгебралық толықтауыштарын есептейік:
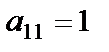 ,
,  ,
,  ,
,
 ,
, 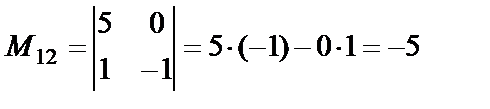
 ,
,
 ,
,  ,
,  .
.
15.Анықтауыштың қасиеттері? 1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді:
 .
.
Теңдіктің дұрыстығын анықтауыштарды есептеу арқылы тексеруге болады.
2-қасиет.Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейткішті анықтауыш алдына шығарамыз:

 .
.
Теңдіктің дұрыстығына берілген матрицаны екінші жол бойынша жіктеп тексеруге болады.
3-қасиет.Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:

Теңдіктің дұрыстығын екінші анықтауышты бірінші жол бойынша жіктеп тексеруге болады.
4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең. Үшінші ретті анықтауыштың бірінші және екінші жолдары бірдей болсын:
 =0.
=0.
Теңдіктің дұрыстығын осы екі жолдың орндарын алмастырып 3-қасиетті қолданып тек.болады.
5-қасиет.Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді. Үшінші ретті анықтауыштың бірінші жолын 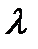 -ға көбейтіп екінші жолға қосайық:
-ға көбейтіп екінші жолға қосайық:
 .
.
Теңдіктің дүрыстығын екінші анықтауышты мынадай






