№1 Найдите пределы функций:
Вариант 1. Вариант 2.
а) 
| г) 
| а) 
| г) 
|
б) 
| д) 
| б) 
| д) 
|
в) 
| в) 
|
№2 Найдите пределы


№3 Найдите пределы

Решение типового варианта
№2

№3

Практическое занятие №3
Тема: Дифференцирование элементарных функций. Нахождение производной сложной функции
Цель: Проверить на практике знание понятия производной функции, умение находить производные элементарных функций, сложных функций, пользуясь таблицей производных и правилами дифференцирования, понятием сложная функция. Закрепить навык нахождения производной и дифференциалов высшего порядка.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Учебник. Богомолов Н.В. «Математика». – М.: Дрофа, 2009.
Индивидуальные карточки с вариантом практической работы.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Ход практического занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности обучающихся к занятию;
3.Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
› Повторить теоретический материал по теме «Дифференцирование элементарных функций. Нахождение производной сложной функции.»
› Рассмотреть примеры решения типовых заданий.
› Выполнить практическую №3.
› Ответить на контрольные вопросы.
Теоретический материал и примеры нахождения производной элементарных функций, сложной функции, производных и дифференциалов высших порядков
I.Производные элементарных функций
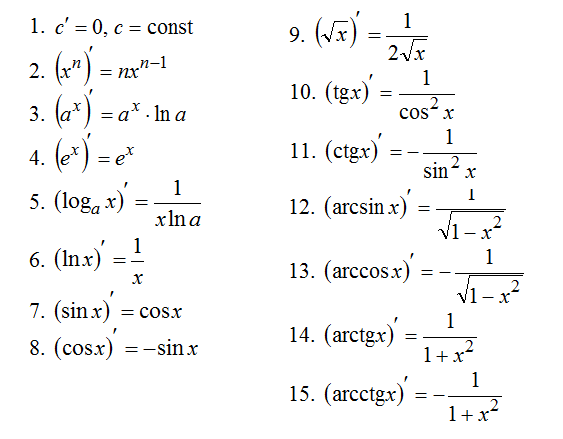
II.Правила дифференцирования
1. (Cu)’ = C(u)’;
2. (u + v – w)’ =u’ + v’ – w’;
3. (uv)’ = u’v + uv’;
4. 
III. Примеры вычисления производных элементарных функций
Задание. Найти производную функции 
Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:
 Ответ.
Ответ. 


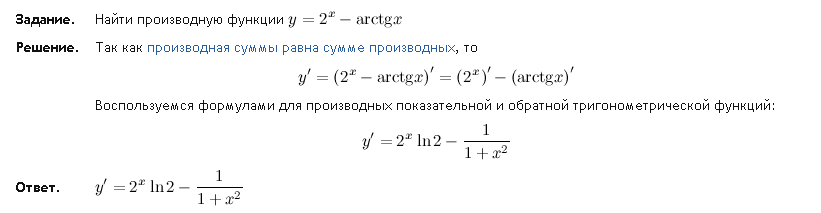

Производная произведения


Производная дроби



Сложная функция
Таблица производных сложных функций
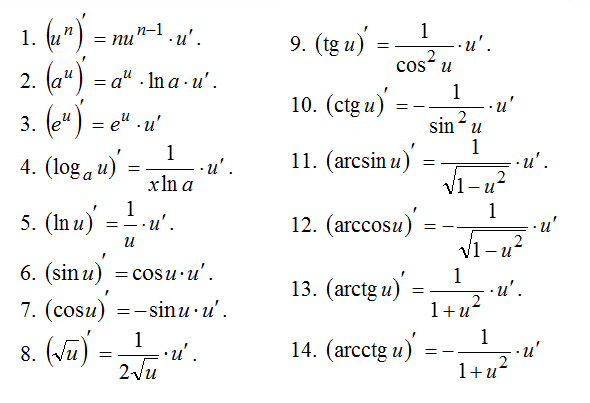
Примеры вычисления производных сложных функций








Контрольные вопросы
1. Запишите правила вычисления производных.
2. Запишите по памяти производные элементарных функций.
3. Запишите по памяти производные сложных функций.






