Раскрытие неопределенностей

Раскрыть неопределенность - это значит определить поведение выражения, приводящего к данной неопределенности, и найти его предел. Рассмотрим несколько приемов раскрытия неопределенностей различного типа

1. Неопределённость , где с - постоянная

Если получаем неопределённость то предел будет равен так как отношение постоянной к бесконечно малой равно

Пример 3. Найди предел функции

Решение:

Ответ:

2. Неопределённость , где с – постоянная

Если получаем неопределённость 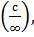то предел будет равен так как отношение постоянной к бесконечно большой, есть величина бесконечно малая.

Пример 4. Найди предел функции

Ответ: 0.

3. Неопределённость

Для раскрытия неопределённостей вида , когда мы имеем дело с рациональными и иррациональными выражениями будем применять два способа.

1. Если в числители и знаменатели дроби стоят целые рациональные выражения, то раскладываем числитель и знаменатель дроби на множители и затем сокращаем дробь. Находим предел полученной функции.

Пример 5. Вычислить предел: .

Решение: При подстановке предельного значения аргумента х = 3 числитель и знаменатель дроби стремятся к нулю. Имеет место неопределенность . Разложим выражение в числителе и знаменателе и произведем сокращение на (х - 3).

х² – 9 =(х – 3)(х + 3)

Ответ:

2. Если в числители (знаменатели) дроби стоит иррациональное выражение, то умножаем числитель и знаменатель дроби на сопряженный множитель иррациональному выражению, затем сокращаем дробь. Находим предел полученной функции.

Пример 6. Вычислить предел: .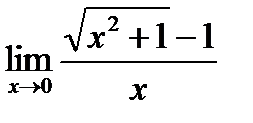

Решение:

Ответ: 0.

4.Неопределённость

При отыскании предела отношения двух целых многочленов относительно х при оба многочлена, стоящие в числители и знаменатели дроби, нужно разделить на хⁿ, где n – наивысшая степень этих многочленов.

Аналогичный приём деления числителя и знаменателя дроби на на хⁿ, где n – наивысшая степень этих многочленов можно применять и для дробей содержащих иррациональности то есть выражения стоящие под знаком корня.

Пример 8. Вычислить предел: .