1. Алгебраическая форма комплексного числа
Запись комплексного числа в виде z = x + i y называется алгебраической
формой комплексного числа.
Комплексное число z = x + i y может быть изображено в декартовой
координатной плоскости XОY либо точкой с абсциссой х и ординатой у,
либо радиус-вектором этой точки: 
2. Тригонометрическая форма комплексного числа
Из рисунка видно, что x=rcosφ, у=rsinφ. Подставляем данные значения х и у в алгебраическую форму комплексного числа имеем, z= rcosφ + rsinφi=r(cosφ + isinφ) то есть z=r(cosφ + isinφ). Такая форма записи комплексного называется тригонометрической формой комплексного числа. 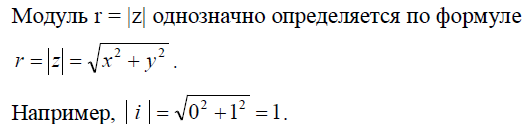


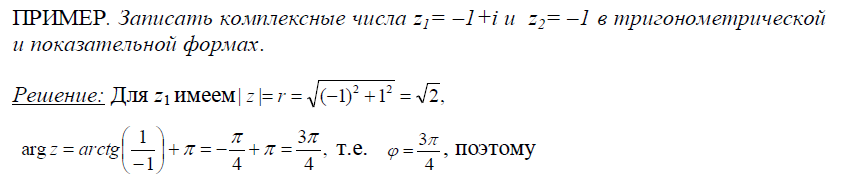
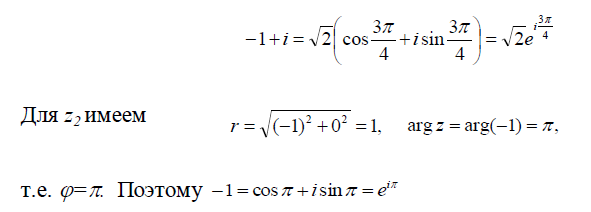
Перечень умений
| № | Умение | Алгоритм |
| 1. | Выполнять действия над комплексными числами (сложение, вычитание, умножение и деление). | Определить, какое выполняется действие над комплексными числами (сложение, вычитание, умножение и деление) и применить соответствующие формулы. |
| 2. | Представлять комплексные числа в тригонометрической и показательной форме. | 1. Найти модуль комплексного числа. 2. Найти главное значение аргумента. 3. Записать полученное число. |
| 3. | Возводить в степень (формула Муавра). | 1. Представить комплексное число в тригонометрической форме; 2. Воспользоваться формулой возведения комплексного числа в степень; 3. Записать полученное число. |
| 4. | Решать алгебраические уравнения на множестве комплексных чисел. | 1. Разложить исходный многочлен на множители; 2. Корни квадратичной функции найти по формуле корней квадратного уравнения. |
Тренинг умений
Пример выполнения упражнения тренинга на умение № 1
Найти 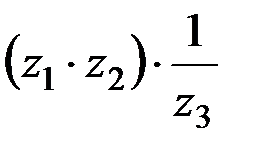 , если
, если 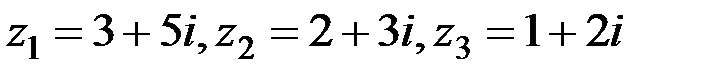 .
.
Решение
| № | Алгоритм | Конкретные действия |
| 1. | Определить, какое выполняется действие над комплексными числами (сложение, вычитание, умножение и деление) и применить соответствующие формулы. | Если  то
1. Умножение выполняется по формуле: то
1. Умножение выполняется по формуле:
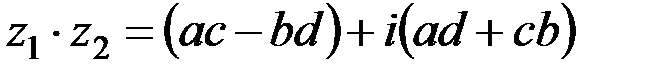 2. Деление выполняется по формуле:
2. Деление выполняется по формуле:
 3. Имеем
3. Имеем 
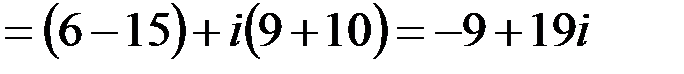 4.
4. 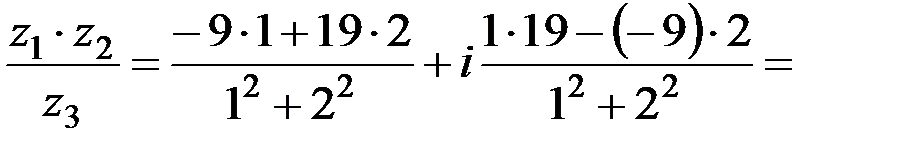
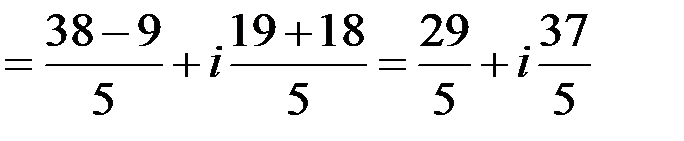
|
Пример выполнения упражнения тренинга на умение № 2.
Представить в тригонометрической и показательной форме комплексное число 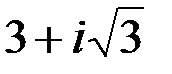 .
.
Решение

Пример выполнения упражнения тренинга на умение № 3
Возвести в степень 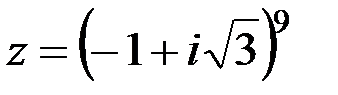 .
.
Решение
| № | Алгоритм | Конкретные действия | |
| 1. | Представить комплексное число в тригонометрической форме. | 1. 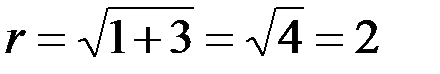 2.
2. 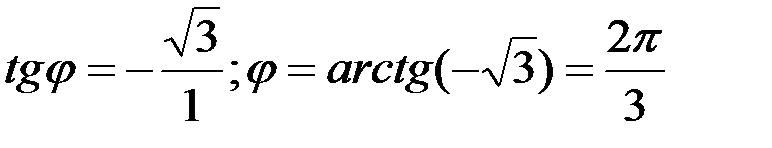 3.
3. 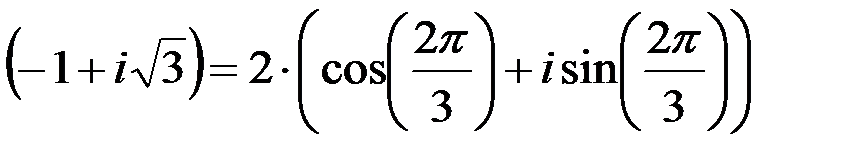
| |
| 2. | Воспользоваться формулой возведения комплексного числа в степень. | 1. 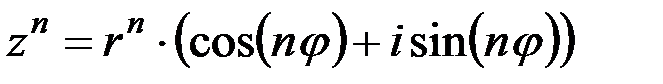 2.
2. 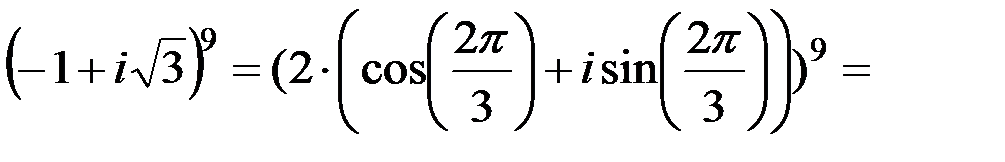
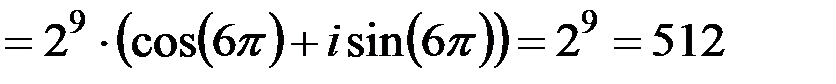
| |
| 3. | Записать полученное число. | 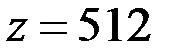
| |
Пример выполнения упражнения тренинга на умение № 4
Решить уравнение 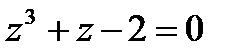 .
.
Решение
| № | Алгоритм | Конкретные действия | |
| 1. | Разложить исходный многочлен на множители. | Очевидно,  – корень этого уравнения.
Разделив многочлен – корень этого уравнения.
Разделив многочлен  на одночлен на одночлен 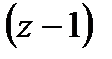 , получим разложение исходного многочлена на множители: , получим разложение исходного многочлена на множители: 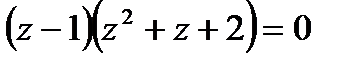 . .
| |
| 2. | Корни квадратичной функции найти по формуле корней квадратного уравнения. | Корни квадратичной функции находим по формуле корней квадратного уравнения: 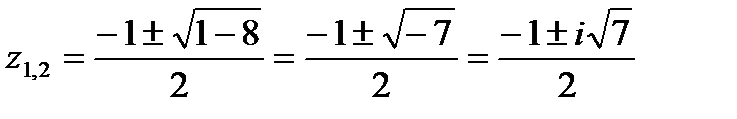 .
Ответ. .
Ответ. 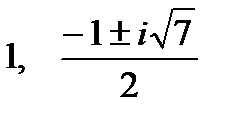 . .
| |






