Для полного исследования функции и построения ее графика можно рекомендовать следующую примерную схему:
1) указать область определения;
2) найти точки разрыва функции, точки пересечения ее графика с осями координат;
3) установить наличие или отсутствие четности, нечетности, периодичности функции;
4) найти асимптоты графика функции;
5) исследовать функцию на монотонность и экстремум;
6) определить интервалы выпуклости и вогнутости;
7) построить график функции.
Решение типового задания.
Пример 1. Найти производную от функции 
.
Решение. Введем вспомогательную функцию u = x 2 + 3 x +1, тогда можно записать 
где u = x 2+3 x +1.
По формуле имеем 
, или, заменив u на его значение:
К такой подробной записи прибегают только на начальной стадии освоения правил дифференцирования, а обычно вспомогательную функцию вводят только мысленно и выполняют указанные действия.
Пример 2. Найти производную от функции 
Решение. Мысленно за u принимаем выражение x 
+ 7 x– 3 и получаем
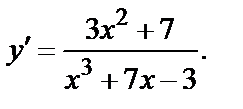
Пример 3. Найти производную от функции 
.
Решение. По правилу дифференцирования произведения записываем:
При вычислении 
принимаем u =1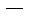 
x 2, тогда
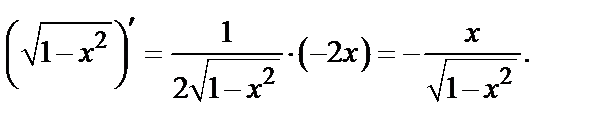
Таким образом,
.
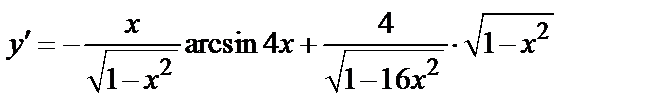Пример 4. Найти производную от функции 
.
Решение. Принимаем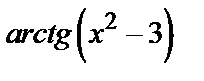 
за вспомогательную функцию u и получим 
При вычислении производной от 
за вспомогательную функцию примем 
:
.
Подставим найденное значение в выражение для 
, окончательно получим: 
Пример 5. Дана функция 
. Найти 
.
Решение. Дифференцируем исходные равенства по t:
По формуле получим
.
Пример 6. Найти производную неявно заданной функции у:
Решение. Дифференцируя обе части уравнения и учитывая, что у – есть функция от х, получим:
или
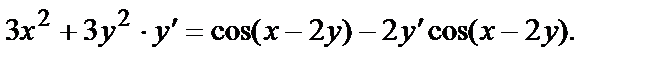
Отсюда находим 
:
или
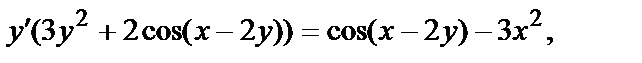
т.е.
Пример 7. Исследовать функцию 
и построить ее график.
Решение. Проведем исследование по общей схеме.
1. Функция определена при всех значениях аргумента x, кроме x =1.
2. Для установления четности или нечетности функции проверим выполнимость равенств 
(тогда 
четная функция) или 
(для нечетной функции) для любых 
и 
из области определения функции:
Следовательно 
и 
то есть данная функция не является ни четной ни нечетной. Также не является периодической.
3. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах 
и 
. В точке x =1 функция терпит разрыв второго рода.
Так как x =1 
точка разрыва функции, причем 
. Поэтому прямая x =1 является вертикальной асимптотой графика.
Для определения уравнения наклонной асимптоты 
воспользуемся формулами:
Тогда
Значит прямая 
есть горизонтальная асимптота графика исследуемой функции.
4. Точки пересечения с осями координат: если 
, то 
; если 
, то 
.
5. Для исследования функции на экстремум найдем ее первую производную:
при 
и 
не существует при 
Тем самым имеем две критические точки: 
. Но точка 
не принадлежит области определения функции, экстремума в ней быть не может.
Для наглядности результаты представим в виде таблицы изменения знака 
:
| 
| 
| 
| |
| 
| + |
| |
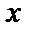
| убывает | min | возрастает | убывает |
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает, во втором интервале–положительна и данная функция возрастает. При переходе через точку x =0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: 
. Значит 
точка минимума.
6. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
при 
и 
не существует при 
. Для наглядности результаты представим в виде таблицы изменения знака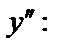 
| 
| 
| 
| 
|
|
| + | + | |
| 
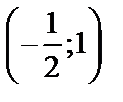
| Перегиб | 
| 
|
На первом интервале вторая производная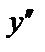 
отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах 
>0, тем самым график является вогнутым. При переходе через точку 
меняет свой знак, поэтому 
абсцисса точки перегиба. Следовательно, 
точка перегиба графика функции.
7. Учитывая полученные результаты, строим график функции:
| y |
| x |
| 0 1 |
|
| B |
| A |
Задачи №121-150:
Найти производные первого порядка данных функций, используя правила вычисления производных:
| 121. | а)  ;
| б)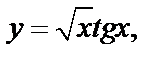 
| в)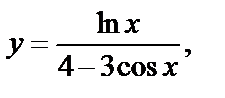 
|
г) 
| д)  .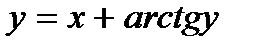
| ||
| 122. | а) 
| б) 
| в)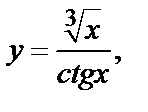 
|
г) 
| д)  .
| ||
| 123. | а) 
| б) 
| в) 
|
г) 
| д)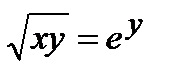 
| ||
| 124. | а)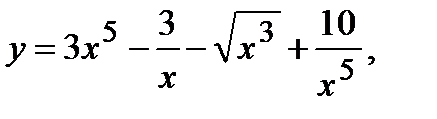 
| б)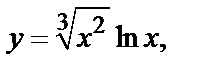 
| в) 
|
г) 
| д) 
| ||
| 125. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 126. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 127. | а) 
| б)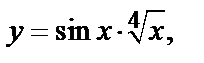 
| в)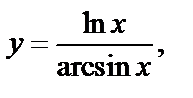 
|
г)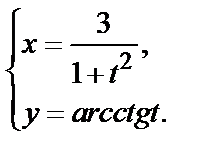 
| д) 
| ||
| 128. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 129. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 130. | а)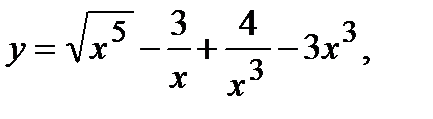 
| б) 
| в) 
|
г)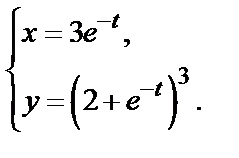 
| д) 
| ||
| 131. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 132. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 133. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 134. | а) 
| б) 
| в) 
|
г)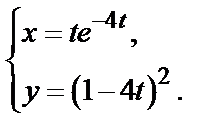 
| д)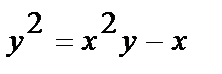 
| ||
| 135. | а)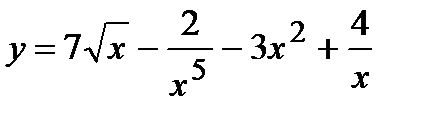 
| б) 
| в)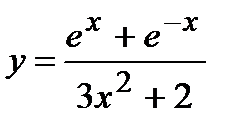 
|
г) 
| д) 
| ||
| 136. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 137. | а) 
| б) 
| в) 
|
г) 
| д)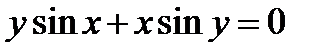 
| ||
| 138. | а) 
| б) 
| в) 
|
г)
| д) 
| ||
| 139. | а) 
| б) 
| в) 
|
| г)
| д)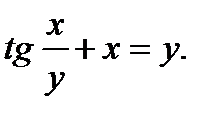 
| ||
| 140. | а) 
| б) 
| в)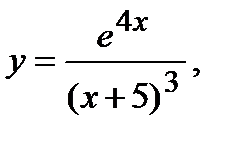 
|
) 
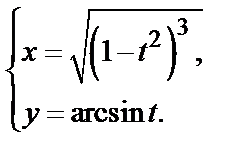
| д) 
| ||
| 141. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 142. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 143. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 144. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 145. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 146. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 147. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 148. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 149. | а) 
| б) 
| в) 
|
г) 
| д) 
| ||
| 150. | а) 
| б) 
| в) 
|
г) 
| д) 
|
Задачи №151-180:
Построить график функции 
, используя общую схему исследования.
| 151. y = x 3 + 6 x 2 + 9 x + 4 | 166. y = x 3 - 6 x 2 + 9 x - 4 |
| 152. y = (2 – x)(x + 1)2 | 167. y = - (x + 1)(x - 2)2 |
153. 
| 168. 
|
| 154. y = x 3 + 3 x 2 - 9 x + 5 | 169. y = x 3 - 3 x 2 - 9 x - 5 |
| 155. y = (x - 6)(x - 3)2 | 170. y = (x + 5)(x + 2)2 |
156. 
| 171. 
|
| 157. y = x 3 + 6 x 2 - 15 x + 8 | 172. y = x 3 - 6 x 2 - 15 x - 8 |
| 158. y = (1 – x)(x + 2)2 | 173. y = - (x + 2)(x - 1)2 |
159. 
| 174. 
|
| 160. y = x 3 - 3 x 2 - 24 x - 28 | 175. y = x 3 + 3 x 2 - 24 x + 28 |
| 161. y = (x + 4)(x - 2)2 | 176. y = (5 – x)(x – 2)2 |
162. 
| 177. 
|
| 163. y = x 3 + 12 x 2 + 45 x + 50 | 178. y = x 3 - 12 x 2 + 45 x - 50 |
| 164. y = (x + 2)(x - 1)2 | 179. y = (x - 4)(x + 2)2 |
165. 
| 180. 
|
