Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых. Острый угол между прямыми 
и 
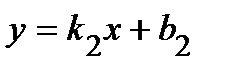определяется по формуле
.
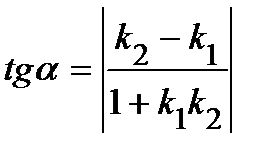Условие параллельности прямых имеет вид 
.
Условие перпендикулярности прямых имеет вид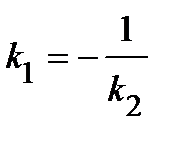 
.
2. Расстояние от точки до прямой. Расстояние от точки М (х 0; у 0) до прямой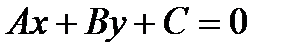 
находится по формуле
.
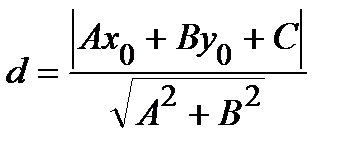3. Пучок прямых. Если пересекающиеся прямые заданы уравнениям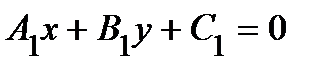и 
и 
, то уравнение
,
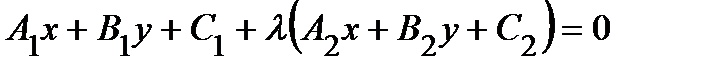где 
– числовой множитель, определяет прямую линию, проходящую через точку пересечения заданных прямых. Давая в последнем уравнении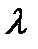 
различные значения, будем получать различные прямые, принадлежащие пучку прямых, центр которого есть точка пересечения прямых.
Решение типового задания.
Даны вершины треугольника А (1; 1), В (5; 4), С (2; 6). Найти:
1) длину стороны АС;
2) уравнение стороны АВ;
3) уравнение высоты СН;
4) уравнение медианы АМ;
5) точку N пересечения медианы АМ и высоты СН;
6) уравнение прямой, проходящей через вершину С параллельно стороне АВ.
Решение.
1) Найдем длину стороны АС.
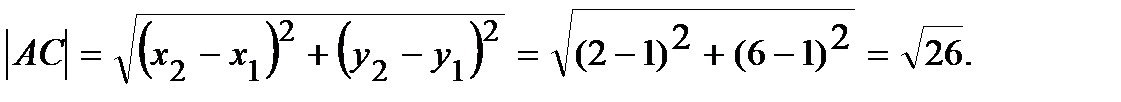
2) Найдем уравнение стороны АВ, используя формулу уравнения прямой, проходящей через две точки: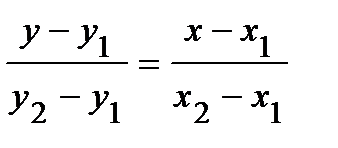 
. Имеем: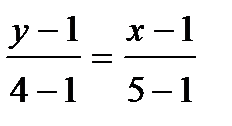 
3 х – 4 у + 1 = 0.
3) Уравнение высоты СН составим как уравнение прямой, имеющей угловой коэффициент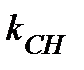 
и проходящей через точку С (х 1; у 1):
.
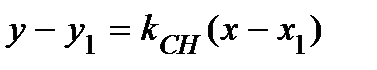Так как 
, то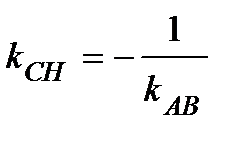 
. Найдем угловой коэффициент прямой АВ из ее уравнения 3 х – 4 у + 1 = 0.
. Отсюда 
, а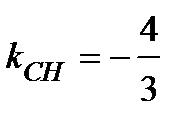 
.
Уравнение высоты СН примет вид:
или 
.
4) Медиана АМ выходит из точки А (1; 1) и по свойствам медианы делит противолежащую сторону пополам, значит М – середина стороны ВС. Найдем координаты точки М по формулам середины отрезка ВС:
, 
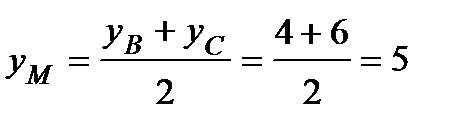
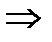М (3,5; 5).
Найдем уравнение медианы АМ, используя формулу уравнения прямой, проходящей через две точки: 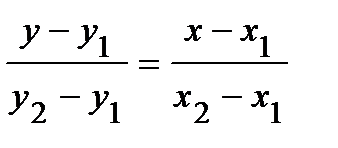. Имеем: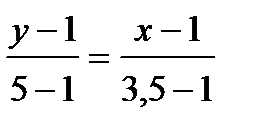 
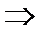4 х – 2,5 у – 1,5 = 0 или
8 х – 5 у – 3 = 0.
5) Чтобы найти точку N пересечения медианы АМ и высоты СН, необходимо решить систему уравнений:
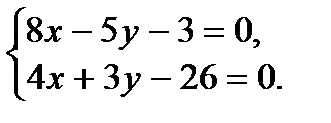Решив эту систему уравнений, получим точку 
.
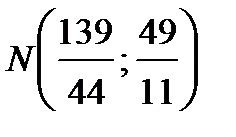Длину высоты найдем по формуле расстояния от точки А до прямой ВС. Для этого составим уравнение прямой ВС, используя формулу уравнения прямой, проходящей через две точки: 
, получаем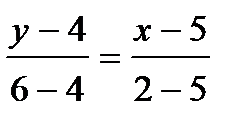 
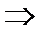2 х + 3 у – 22 = 0.
6) Уравнение прямой, проходящей через вершину С параллельно стороне АВ обозначим СК. Так как СК || АВ, то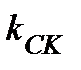 
= 
= 
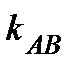. Уравнение прямой, имеющей угловой коэффициент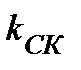 
и проходящей через точку С (х 1; у 1):
.
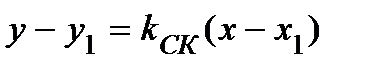Получаем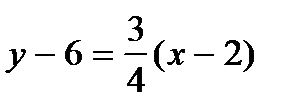 
, тогда уравнение прямой СК имеет вид 4 у – 3 х – 18 = 0.
Задачи №31-60:
Даны координаты вершин треугольника АВС. Найти:
1) длину стороны АС;
2) уравнение стороны АВ;
3) уравнение высоты СН;
4) уравнение медианы АМ;
5) точку N пересечения медианы АМ и высоты СН;
6) уравнение прямой, проходящей через вершину С параллельно стороне АВ.
| 31. А (1; -3), В (0; 7), С (-2; 4) | 46. А (1; 1), В (7; 4), С (4; 5) |
| 32. А (7; 0), В (1; 4), С (-8; -4) | 47. А (2; 0), В (8; 3), С (5; 4) |
| 33. А (0; 2), В (-7; -4), С (3; 2) | 48. А (3; -1), В (9; 2), С (6; 4) |
| 34. А (3; -1), В (11; 3), С (-6; 2) | 49. А (4; -2), В (10; 1), С (7; 2) |
| 35. А (-2; -3), В (0; 7), С (8; 3) | 50. А (0; 2), В (6; 5), С (3; 6) |
| 36. А (1; 2), В (3; 12), С (11; 8) | 51. А (-1; 3), В (5; 6), С (2; 7) |
| 37. А (-4; -1), В (-2; 9), С (6; 5) | 52. А (-2; 4), В (4; 7), С (1; 8) |
| 38. А (5; 4), В (7; 11), С (15; 10) | 53. А (3; -3), В (9; 0), С (6; 1) |
| 39. А (-8; -3), В (4; -12), С (8; 10) | 54. А (-1; 0), В (5; 3), С (2; 4) |
| 40. А (1; 0), В (13; -9), С (7; 13) | 55. А (-2; 3), В (4; 6), С (1; 7) |
| 41. А (1; -1), В (7; 2), С (4; 3) | 56. А (5; -3), В (11; 0), С (8; 3) |
| 42. А (2; -2), В (8; 1), С (5; 2) | 57. А (-4; 6), В (2; 9), С (-1; 10) |
| 43. А (1; 0), В (7; 3), С (4; 4) | 58. А (1; 3), В (7; 6), С (4; 7) |
| 44. А (2; -1), В (8; 2), С (5; 3) | 59. А (4; -1), В (10; 2), С (7; 3) |
| 45. А (3; -2), В (9; 1), С (6; 2) | 60. А (-2; 2), В (4; 5), С (1; 6) |
