Определение. Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число 
, то говорят, что задана числовая последовательность 
:
Числа 
называются членами последовательности, а число – общим членом последовательности.
Определение. Число а называется пределом числовой последовательности , если для любого, даже сколь угодно малого положительного числа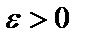 
, найдется такой номер 
, что для всех членов последовательности с номерами 
верно неравенство
.
Обозначается 
.
Последовательность, имеющая предел, называется сходящейся, в противно случае – расходящейся.
Определение. Последовательность называется бесконечно малой, если для любого сколь угодно малого положительного числа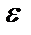 
можно подобрать такой номер N, что, начиная с этого номера (т.е. для всех 
), будет выполнено неравенство
.
Обозначается: б.м. .
Определение.
1. Последовательность называется положительной бесконечно большой, если для любого сколь угодно большого числа M найдется такой номер N, что для всех n, начиная с этого номера, выполняется неравенство 
Обозначается 
2. Последовательность называется отрицательной бесконечно большой, если для любого сколь угодно большого по модулю отрицательного числа M найдется такой номер N, что для всех n, начиная с этого номера, выполняется неравенство 
Обозначается 
Последовательность 
, все члены которой отличны от нуля, - бесконечно малая тогда и только тогда, когда последовательность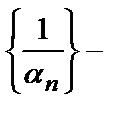 
бесконечно большая.
Кроме того, полезно иметь в виду следующее:
1. Пусть 
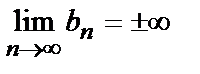. Тогда 
2. Пусть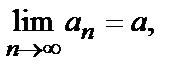 
(в том числе 
), 
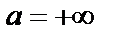(соответственно, 
, в том числе 
), 
Тогда 
(соответственно, 
).
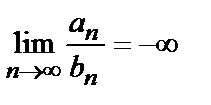Предел функции
Определение. Окрестностью точки 
называется любой интервал с центром в точке 
.
Определение. Число А называется пределом функции f (x) при 
, если для любого 
найдется 
такое, что 
при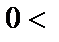 
Это записывают так: 
.
Практическое вычисление пределов основывается на следующих свойствах.
Если существуют 
и 
, то
1) 
;
2) 
;
3) 
(при 
).
Определение.
1. Число А называется пределом функции f (x) при 
, если для любого числа 
найдется такое число 
, что для всех значений 
выполняется неравенство .
Обозначается: 
2. Число А называется пределом функции f (x) при 
, если для любого числа найдется такое число , что для всех значений выполняется неравенство .
Обозначается: 
Определение.
1. Пусть функция f (x) определена в правой полуокрестности точки а, т.е. на некотором интервале 
, где 
. Тогда говорят, что число А называется пределом функции f(x) справа в точке а (или правосторонним пределом), если для любой последовательности 
, сходящейся к а и такой, что все ее члены больше, чем а, соответствующая последовательность значений функции 
сходится к числу А.
Обозначается: 
2. Пусть функция f (x) определена в левой полуокрестности точки а, т.е. на некотором интервале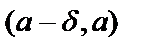 
, где . Тогда говорят, что число А называется пределом функции f(x) слева в точке а (или левосторонним пределом), если для любой последовательности , сходящейся к а и такой, что все ее члены меньше, чем а, соответствующая последовательность значений функции сходится к числу А.
Обозначается: 
Очевидно, что 
существует в том и только в том случае, когда существуют и односторонние пределы 
и 
, причем все три числа равны, т.е.
= 
= 
.
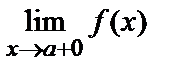Замечательные пределы.
Первый замечательный предел
Второй замечательный предел
Непрерывность функции
Определение. Функция 
называется непрерывной при х = а
(в точке а), если:
1) функция 
определена в точке а и ее окрестности;
2) существует конечный предел функции в точке а;
3) этот предел равен значению функции в точке а, т.е.
.
Определение. Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Определение. Точка а, в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
Если в точке а существуют конечные пределы 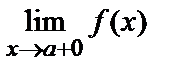и , такие что 
, то а называется точкой разрыва первого рода. Если в точке а существует конечный предел 
, а 
не определено или 
, то эта точка называется точкой устранимого разрыва. Точки разрыва первого рода функции, не являющиеся точками устранимого разрыва, называются точками скачка этой функции, при этом величина 
называется скачком функции в точке а.
Если хотя бы один из пределов 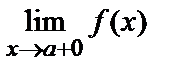и не существует или равен бесконечности, то точку а называют точкой разрыва второго рода.
Решение типового задания.
Пример 1. Найти 
Решение. Так как пределы числителя и знаменателя при 
равны нулю, то мы имеем неопределенность вида 
. «Раскроем» эту неопределенность, разложив числитель и знаменатель на множители и сократив их далее на общий множитель (x +2):
Пример 2. Найти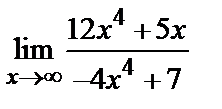 
.
Решение. Подстановка предельного значения аргумента приводит к неопределенности вида 
. Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т.е. на x 4. В результате получим
поскольку при 
функции 5/ x 3 и 7/ x 4 являются бесконечно малыми.
Пример 3. Найти 
Решение. Здесь мы также имеем неопределенность вида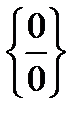 
.
Домножим числитель и знаменатель дроби на выражение, сопряженное к числителю:
Пример 4. Найти 
Решение. Так как 
под знаком предела, то
Пример 5. Найти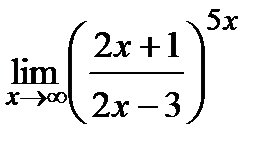 
Решение.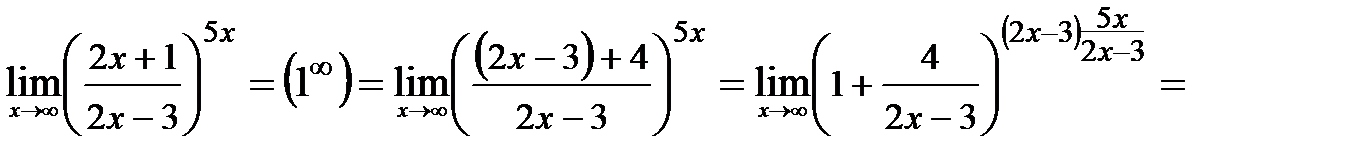 
Задачи №91-120:
Найти пределы (не применяя правило Лопиталя):
| 91. | а) | 
| б) | 
| |||
| в) | 
| г) | 
| ||||
| 92. | а) |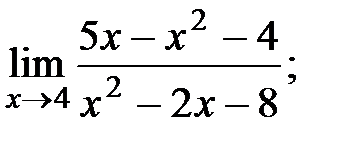 
| б) | 
| |||
| в) | 
| г) | 
| ||||
| 93. | а) | 
| б) | 
| |||
| в) | 
| г) | 
| ||||
| 94. | а) | 
| б) | 
| |||
| в) |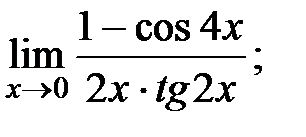 
| г) | 
| ||||
| а) | 
| б) | 
| ||||
| в) | 
| г) | 
| ||||
| 96. | а) | 
| б) | 
| |||
| в) | 
| г) | 
| ||||
| 97. | а) |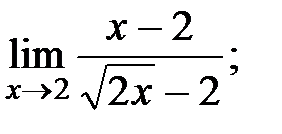 
| б) | 
| |||
| в) | 
| г) | 
| ||||
| 98. | а) | 
| б) | 
| |||
| в) | 
| г) | 
| ||||
| 99. | а) | 
| б) | 
| |||
| в) |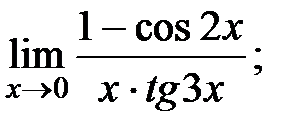 
| г) | 
| ||||
| 100. | а) | 
| б) | 
| |||
| в) | 
| г) | 
| ||||
101. а) 
| б) 
| ||||||
в)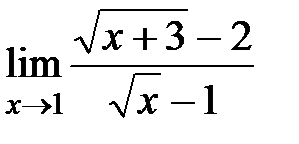 
| г) 
| ||||||
102. а) 
| б) 
| ||||||
в)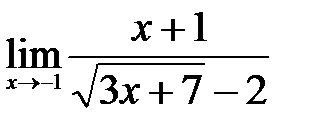 
| г) 
| ||||||
103. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
104. а) 
| б)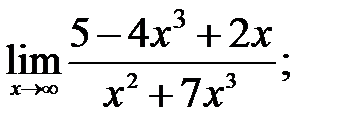 
| ||||||
в) 
| г) 
| ||||||
105. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
106. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
107. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
108. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
109. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
110.а) 
| б)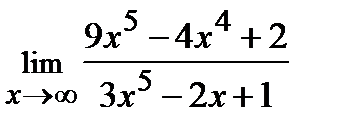 
| ||||||
в) 
| г) 
| ||||||
111. а) 
| б)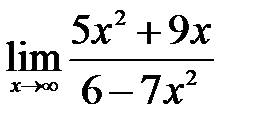 
| ||||||
в) 
| г) 
| ||||||
112. а) 
| б)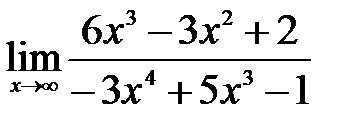 
| ||||||
| в)
| г)
| ||||||
113. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
114.а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
115. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
116. а) 
| б)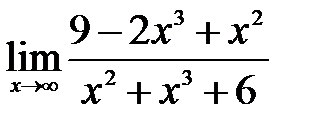 
| ||||||
| в)
| г)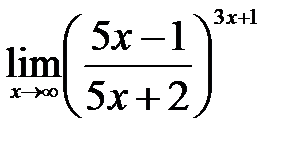 
| ||||||
117. а) 
| б)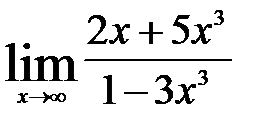 
| ||||||
в) 
| г) 
| ||||||
118.а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
119. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
120. а) 
| б) 
| ||||||
в) 
| г) 
| ||||||
