Определение. Проекцией вектора на ось называется число, равное длине составляющей, взятое со знаком плюс, если составляющая соноправлена с осью и со знаком минус в противном случае (рис. 1)
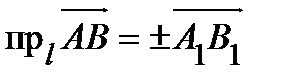 .
.
Рис. 1
Теорема 6. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью
 .
.
Теорема 7. Если вектор  умножить на число
умножить на число 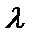 , то его проекция на ось также умножится на это число
, то его проекция на ось также умножится на это число
 .
.
Теорема 8. Проекция суммы двух векторов на ось равна сумме слагаемых векторов на ту же ось
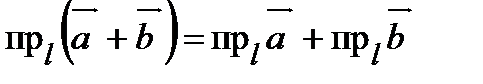 .
.
Определение. Координатами вектора  называют его проекции на координатные оси Ох, Оу, Oz. Записывают
называют его проекции на координатные оси Ох, Оу, Oz. Записывают  или
или  – разложение вектора по ортам
– разложение вектора по ортам  ,
,  ,
,  координатных осей Ох, Оу, Oz.
координатных осей Ох, Оу, Oz.
Определение. Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат
 .
.
Определение. Направляющими косинусами вектора называются косинусы углов 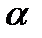 ,
,  ,
,  , образованных этим вектором с осями координат Ох, Оу, Oz:
, образованных этим вектором с осями координат Ох, Оу, Oz:
 ,
, 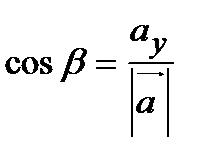 ,
,  , причем
, причем  .
.
Действия над векторами, заданными своими координатами
Пусть даны векторы  и
и  :
:
1) при сложении векторов их одноименные координаты складываются
 или
или  ;
;
2) при умножении вектора на число все его координаты умножаются на это число
 или
или  , где
, где  .
.
Определение. Два вектора  и
и  называются равными, если выполняются равенства
называются равными, если выполняются равенства
 .
.
Необходимым и достаточным условием коллинеарности векторов  и
и  является пропорциональность их координат
является пропорциональность их координат
 , где
, где 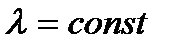 .
.
Если известны координаты начала А (х 1, у 1, z 1) и конца B (х 2, у 2, z 2) вектора  , то его координаты определяются
, то его координаты определяются
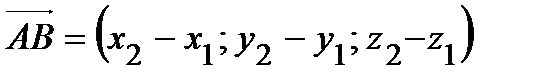 .
.
Длину вектора, заданного координатами начала и конца, вычисляют по формуле
 .
.
Скалярное произведение
Определение. Скалярным произведением  векторов
векторов  и
и  называется число, равное произведению их длин на косинус угла между ними:
называется число, равное произведению их длин на косинус угла между ними:
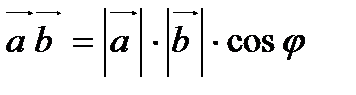 или
или  .
.
Свойства скалярного произведения:
10.  – переместительный закон;
– переместительный закон;
20.  – распределительный закон;
– распределительный закон;
30.  – сочетательный закон, где
– сочетательный закон, где  ;
;
40 скалярное произведение равно нулю тогда и только тогда, когда векторы  и
и  перпендикулярны, т.е.
перпендикулярны, т.е.  ;
;
50. скалярный квадрат вектора равен квадрату его длины:  .
.
Пусть даны два вектора 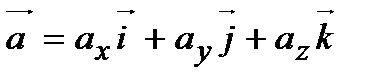 и
и 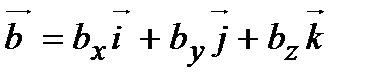 . По свойствам 40 и 50 имеем
. По свойствам 40 и 50 имеем 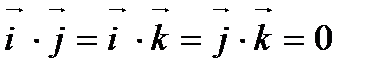 ;
;  .
.
Скалярное произведение двух векторов равно сумме произведений их одноименных координат
 .
.
Условие перпендикулярности двух ненулевых векторов  и
и  :
:
 .
.
Косинус угла между векторами определяется по формуле:
 .
.
Проекция вектора  на направление, заданное вектором
на направление, заданное вектором 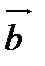 , вычисляется по формуле
, вычисляется по формуле
 .
.
Векторное произведение
Определение. Векторным произведением вектора 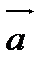 на вектор
на вектор  называют такой вектор
называют такой вектор  , который строится по следующему правилу (рис. 2):
, который строится по следующему правилу (рис. 2):
1) вектор  перпендикулярен векторам
перпендикулярен векторам  и
и  и направлен таким образом, что кратчайший поворот от
и направлен таким образом, что кратчайший поворот от  к
к  виден из его конца совершающимся против часовой стрелки;
виден из его конца совершающимся против часовой стрелки;
2) длина вектора  равна произведению длин векторов
равна произведению длин векторов  и
и  на синус угла
на синус угла 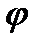 между ними:
между ними:  .
.
Рис. 2
Векторное произведение  и
и  обозначается
обозначается  .
.
Свойства векторного произведения:
10. 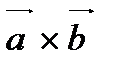 =
=  (т.е. векторное произведение не обладает переместительным свойством).
(т.е. векторное произведение не обладает переместительным свойством).
20.  , если
, если  , либо
, либо  , либо
, либо  ǀǀ
ǀǀ  (коллинеарность ненулевых векторов).
(коллинеарность ненулевых векторов).
30.  , где
, где  (сочетательное свойство по отношению к скалярному множителю).
(сочетательное свойство по отношению к скалярному множителю).
40.  (распределительное свойство).
(распределительное свойство).
Модуль векторного произведения двух неколлинеарных векторов 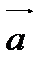 и
и 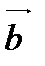 равен площади параллелограмма, построенного на этих векторах.
равен площади параллелограмма, построенного на этих векторах.
Векторные произведения координатных ортов 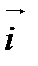 ,
,  ,
,  :
:
 ,
,
 ;
;  ;
;  .
.
Пусть векторы 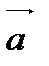 и
и 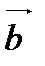 заданы своими координатами:
заданы своими координатами:  ,
,  . Тогда векторное произведение удобнее находить по формуле
. Тогда векторное произведение удобнее находить по формуле
 .
.
Смешанное произведение
Определение. Смешанным произведением векторов  ,
,  и
и  называется скалярное произведение вектора
называется скалярное произведение вектора  на вектор
на вектор  , т.е.
, т.е.  .
.
Смешанное произведение трех векторов  ,
,  и
и  по модулю равно объему параллелепипеда, построенного на этих векторах.
по модулю равно объему параллелепипеда, построенного на этих векторах.
Свойства смешанного произведения:
10. Смешанное произведение трех векторов равно нулю, если:
а) хоть один из перемножаемых векторов равен нулю;
б) два из перемножаемых векторов коллинеарны;
в) три ненулевых вектора параллельны одной и той же плоскости (компланарность).
20. Смешанное произведение не изменяется, если в нем поменять местами знаки векторного  и скалярного
и скалярного  умножения, т.е.
умножения, т.е. 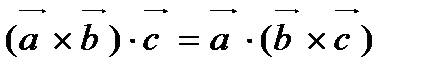 . В силу этого свойства смешанное произведение векторов
. В силу этого свойства смешанное произведение векторов  ,
, 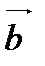 и
и  будем записывать в виде
будем записывать в виде  .
.
30. Смешанное произведение не изменяется, если переставлять перемножаемые векторы в круговом порядке:
 .
.
40. При перестановке любых двух векторов смешанное произведение изменяет только знак:
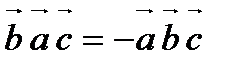 ;
;  ;
;  .
.
Пусть векторы  ,
,  и
и  заданы своими координатами:
заданы своими координатами:  ,
,  ,
,  . Тогда смешанное произведение
. Тогда смешанное произведение  равно определителю третьего порядка, составленному из координат векторов
равно определителю третьего порядка, составленному из координат векторов  ,
, 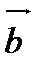 и
и  :
:
 .
.
Из свойств смешанного произведения трех векторов вытекает следующее:
1) необходимым и достаточным условием компланарности трех векторов служит условие  ;
;
2) объем V 1 параллелепипеда, построенного на векторах 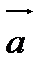 ,
,  и
и  , и объем V 2 образованной ими треугольной пирамиды находятся по формулам:
, и объем V 2 образованной ими треугольной пирамиды находятся по формулам:
 ,
,  .
.
Решение типового задания.
Даны координаты вершин пирамиды:  Вычислить:
Вычислить:
1) объем пирамиды;
2) длину ребра 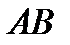 ;
;
3) площадь грани  ;
;
4) угол между ребрами 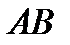 и
и  .
.
Решение:
1) Объем пирамиды вычисляется по формуле:  .
.
Найдем векторы 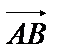 ,
,  и
и  , совпадающие с ребрами пирамиды, сходящимися в вершине А:
, совпадающие с ребрами пирамиды, сходящимися в вершине А:
 ,
,  ,
,  .
.
Находим смешанное произведение этих векторов:
 .
.
Так как объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах  ,
,  и
и 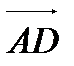 , то
, то  (куб. ед.).
(куб. ед.).
2. Длина ребра вычисляется по формуле: 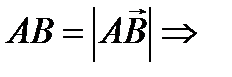
 .
.
3. Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах 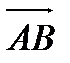 и
и  , поэтому находим векторное произведение этих векторов:
, поэтому находим векторное произведение этих векторов:
 .
.
Следовательно,  (кв. ед.).
(кв. ед.).
4. Угол между ребрами 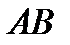 и
и  вычисляется по формуле:
вычисляется по формуле: 
Задачи №61-90:
Даны координаты вершин пирамиды 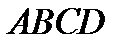 . Вычислить: 1) объем пирамиды;
. Вычислить: 1) объем пирамиды;
2) длину ребра 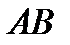 ;
;
3) площадь грани  ;
;
4) угол между ребрами 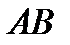 и
и  .
.
Координаты вершин пирамиды для соответствующих номеров задач следующие:
61. 
62. 
63. 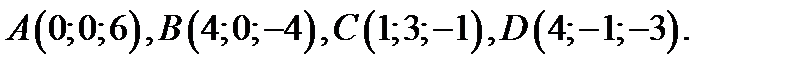
64. 
65. 
66. 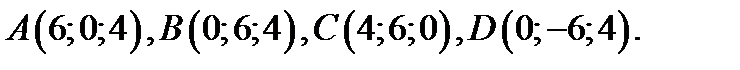
67. 
68. 
69. 
70. 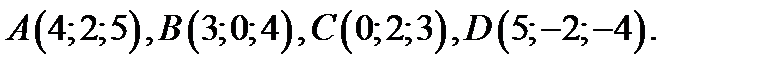
71. 
72. 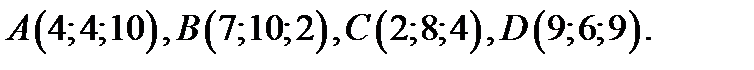
73. 
74. 
75. 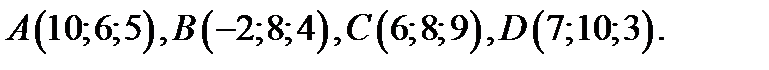
76. 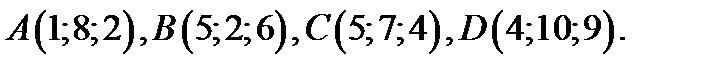
77. 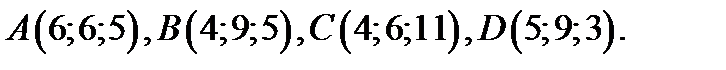
78. 
79. 
80. 
81. 
82. 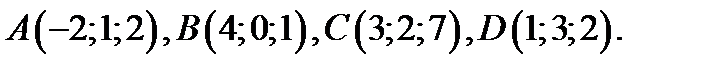
83. 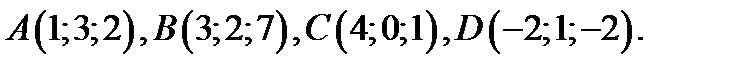
84. 
85. 
86. 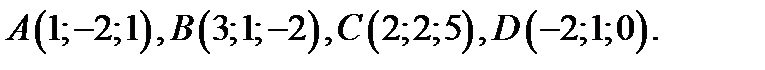
87. 
88. 
89. 
90. 
РАЗДЕЛ IV. ФУНКЦИИ. ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
Функция. Основные понятия
Определение. Пусть даны два непустых множества X и Y. Если каждому элементу x из множества Х по определенному правилу ставится в соответствие один и только один элемент у из Y, то говорят, что на множестве Х задана функция (или отображение) со множеством значений Y.
Это можно записать так:  или
или 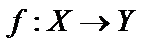 , где множество Х называется областью определения функции (D (f)), а множество Y, состоящее из всех чисел вида
, где множество Х называется областью определения функции (D (f)), а множество Y, состоящее из всех чисел вида  ,
,  множеством значений функции (E (f)).
множеством значений функции (E (f)).
Определение. Графиком функции  называется множество точек
называется множество точек  плоскости
плоскости 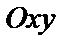 , координаты которых удовлетворяют функциональной зависимости
, координаты которых удовлетворяют функциональной зависимости  .
.
Определение.
1. Функция называется четной, если множество D (f) симметрично относительно нуля и для любого 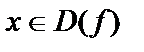 справедливо равенство
справедливо равенство 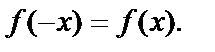 График четной функции симметричен относительно оси
График четной функции симметричен относительно оси 
2. Функция называется нечетной, если множество D (f) симметрично относительно нуля и для любого 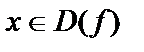 справедливо равенство
справедливо равенство  График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат.
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
Определение. Функция  называется периодической, если существует число
называется периодической, если существует число  что для любого
что для любого 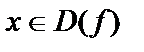 справедливы условия:
справедливы условия:
1) 
2) 
Число  называется периодом функции
называется периодом функции  .
.
Определение. Если функция  определена на области D, G – ее область значений, функция
определена на области D, G – ее область значений, функция  определена на области G, то функция
определена на области G, то функция 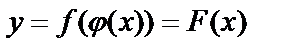 называется сложной функцией. Функцию
называется сложной функцией. Функцию 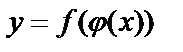 называют композицией двух функций
называют композицией двух функций  и
и  .
.
Сложная функция может быть композицией большего числа функций: трех, четырех и т.д. Например, функция  – композиция двух функций
– композиция двух функций  и
и  функция
функция 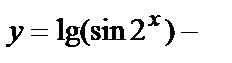 композиция трех функций
композиция трех функций  .
.
К основным элементарным функциям относятся:
1) степенная функция y =  , где
, где  ;
;
2) показательная функция y = ax, где  ;
;
3) логарифмическая функция y =  , где
, где  ;
;
4) тригонометрические функции: 
 ,
, 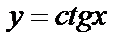 ;
;
5) обратные тригонометрические функции:  y = arccos x, y = arctg x, y = arcctg x.
y = arccos x, y = arctg x, y = arcctg x.
Определение. Функция 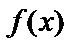 называется неубывающей (невозрастающей) на множестве
называется неубывающей (невозрастающей) на множестве  , если для любых значений
, если для любых значений  таких, что
таких, что  справедливо неравенство
справедливо неравенство 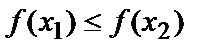 (соответственно,
(соответственно,  ).
).
Определение. Функция 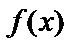 называется монотонной, если она невозрастающая или неубывающая.
называется монотонной, если она невозрастающая или неубывающая.
Определение. Функция 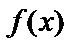 называется возрастающей (убывающей) на множестве
называется возрастающей (убывающей) на множестве  , если для любых значений
, если для любых значений  таких, что
таких, что  справедливо неравенство
справедливо неравенство  (соответственно,
(соответственно, 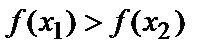 ).
).
Определение. Функция 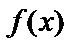 называется строго монотонной, если она возрастающая или убывающая.
называется строго монотонной, если она возрастающая или убывающая.






