Пусть дана система n линейных уравнений с n переменными:
или в матричной форме 
.
Определение. Определитель матрицы A обозначим 
и назовем определителем системы:
.
Определение. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае 
.
Умножив обе части уравнения 
слева на матрицу А -1, получим 
. Поскольку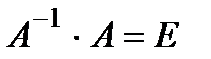 
и 
, то
.
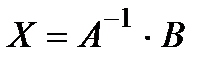Определение. Отыскание решения системы по формуле 
называют матричным способом решения системы.
Таким образом, чтобы решить систему уравнений матричным способом, нужно:
1. Найти обратную матрицу А -1.
2. Найти произведение обратной матрицы А -1 на матрицу-столбец свободных членов B, т.е.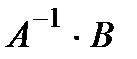 
.
3. Пользуясь определением равных матриц, записать ответ.
Если в определителе системы 
заменить поочередно столбцы коэффициентов при 
на столбец свободных членов, то получим n определителей (для n неизвестных):
, 
,…, 
.
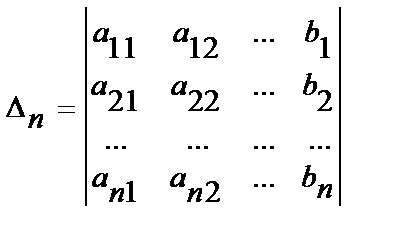Тогда получим формулы для решения системы n линейных уравнений с n неизвестными:
.
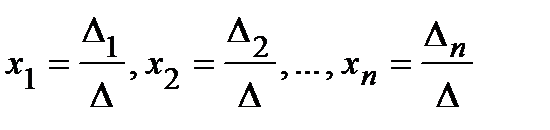Определение. Формулы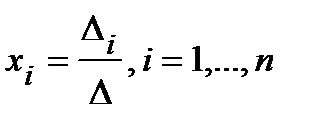 
называются формулами Крамера.
Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов.
I этап (прямой ход).
С помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (треугольного) вида:
где 
, 
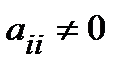, i = 1,…, k. Коэффициенты 
называются главными элементами системы.
II этап (обратный ход).
Из ступенчатой системы последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное 
через остальные неизвестные (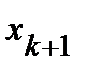
,…, 
). Затем подставляем значение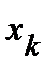 
в предпоследнее уравнение системы и выражаем 
через (
,…, 
); затем находим 
,…, 
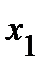. Придавая свободным неизвестным (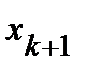,…, ) произвольные значения, получим бесчисленное множество решений системы.
Замечание. Если ступенчатая система оказывается треугольной, т.е. 
, то исходная система имеет единственное решение. Из последнего уравнения находим 
, из предпоследнего уравнения 
, далее поднимаясь по системе вверх, найдем все остальные неизвестные (
,…, 
).
Решение типового задания.
Пример 1. Решить матричным способом систему уравнений
Решение.
Составим матричное решение 
, где
, 
, 
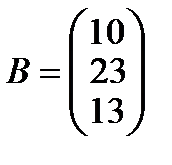
тогда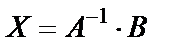 
. Вычислим обратную матрицу А -1.
Находим
.
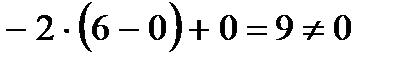Вычислим алгебраические дополнения Aij элементов матрицы A:
 ;
| 
| 
|
 ;
|  ;
|  ;
|
 ;
|  ;
|  .
|
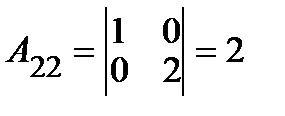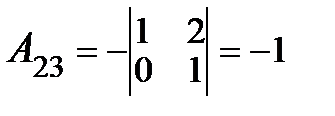Составим матрицу 
и транспонируем ее 
.
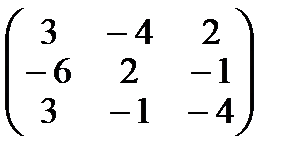Запишем обратную матрицу 
. Следовательно,
.
Ответ: 
Пример 2. Решить систему уравнений по формулам Крамера:
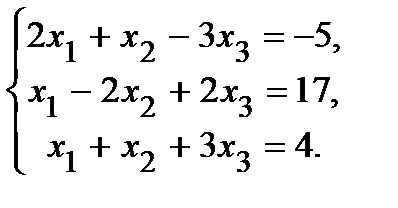
Решение.
Вычислим определитель системы:
, а также
, 
Подставляя найденные значения определителей в формулы Крамера, получаем искомое решение системы:
.
Ответ: 
Пример 3. Решить систему уравнений методом Гаусса:
Решение.
Переставим третье уравнение на место первого:
Запишем расширенную матрицу:
.
Чтобы в 1-м столбце получить a 21 = a 31 = 0, умножим 1-ю строку сначала на 2, а затем на 3 и вычтем результаты из 2-й и 3-й строк:
.
Умножим 2-ю строку на 8, а 3-ю строку умножим на 3, затем полученные результаты вычтем из 3-й строки 2-ю строку:
.
Запишем новую эквивалентную систему, которой соответствует расширенная матрица:
Выразим переменную z из 3-го уравнения, у – из 2-го уравнения, переменную x из 1-го уравнения:
Ответ: x = 1, y = 2, z = 3.
Задачи №1-30:
Решите систему линейных уравнений тремя способами: а) по формулам Крамера;
б) с помощью обратной матрицы; в) методом Гаусса.
1. 
| 2.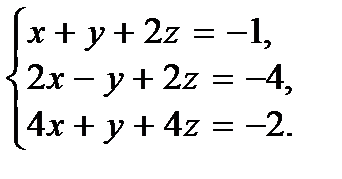 
|
3. 
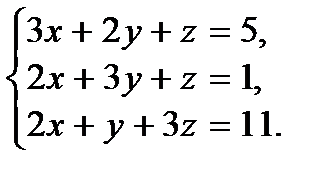
| 4. 
|
5. 
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12. 
|
13. 
| 14. 
|
15. 
| 16. 
|
17. 
| 18.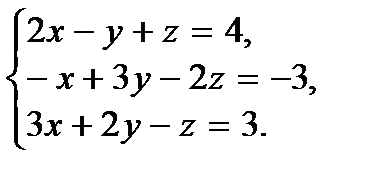 
|
19. 
| 20. 
|
21. 
| 22. 
|
23. 
| 24. 
|
25. 
| 26. 
|
27. 
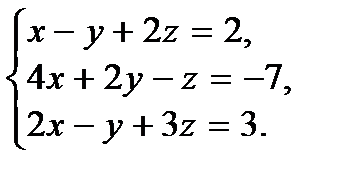
| 28. 
|
29. 
| 30. 
|
