При быстром расширении или сжатии газа тепло не успевает пройти через стенки сосуда в окружающую среду, так что процесс такого расширения или сжатия близок к адиабатному. Давление газа при его сжатии растет как вследствие уменьшения объема, так и вследствие повышения его температуры, вызванного совершаемой над газом работой.
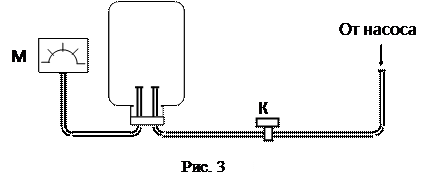 |
Для определения коэффициента Пуассона g используется наполненный воздухом стеклянный сосуд (рис. 3), соединенный с ручным нагнетательным насосом и манометром М. Кран К позволяет отключить насос от баллона и соединить баллон с внешней средой.
Если с помощью насоса накачать в сосуд небольшое количество воздуха, то давление в нем повысится. Одновременно повысится и температура воздуха, но через несколько минут в результате теплообмена с окружающей средой температура воздуха в сосуде сравняется с температурой окружающей среды, т.е. станет равной Т 1, К. Назовем это состояние первым и обозначим его точкой 1 (рис. 4).
Давление в сосуде в первом состоянии (при закрытом кране К и после того, как температура установится) р 1 = Р атм + h 1, где h 1 – разность между давлением в сосуде и атмосферным давлением, измеренная манометром и выраженная в тех же единицах измерения, что и Р атм. Удельный объем газа будет равен v 1 = V / m, где V – объем сосуда; m – масса газа в нем.
 |
Если быстро открыть кран К, то часть воздуха из сосуда выйдет наружу, в результате чего произойдет адиабатное расширение воздуха, находящегося в сосуде. Кран К нужно закрыть, как только манометр покажет, что давление в сосуде сравнялось с атмосферным. Параметрами второго состояния воздуха в сосуде будут: давление р 2 = Р атм, Т 2 < Т 1, v 2 > v 1. Точка 2 на рис.4, характеризующая второе состояние воздуха, будет лежать на одной адиабате с точкой 1.
Через несколько минут после закрытия крана К в результате теплообмена с окружающей средой температура воздуха в сосуде станет равной температуре окружающего воздуха Т 3 = Т к. Удельный объем газа не изменится: v 3 = v 2, а давление в сосуде повысится до р 3 = Р атм + h 2.
Избыточное давление h 2 должно быть записано по показанию манометра.
Точка 3 на рис.4, характеризующая третье состояние воздуха в сосуде, лежит выше точки 2 на одной изохоре (линии постоянного объема) с ней. Точки 3 и 1 лежат на изотерме, которой соответствует температура Т 1. При адиабатном расширении, т.е. при переходе газа из состояния 1 в состояние 2, справедливо уравнение Пуассона.
Из нашего опыта
р 1 ×T к g / 1 – g = p 2 ×T 2 g / g – 1. (1)
Для изохорного процесса перехода газа из второго состояния в третье получим
 . (2)
. (2)
Подставив в уравнение (1) выражение  из (2), получим
из (2), получим
 или
или  .
.
Прологарифмировав это уравнение, найдем
(1– g)(lg р 1 –lg р 2) = g(lg р 2 –lg р 3),
откуда  .
.
Заменив величины р 1, р 2, р 3 уже известными выражениями, получим

Поскольку при больших значениях аргумента прирост логарифма пропорционален малому приросту аргумента, это уравнение можно упростить:
 (3)
(3)
и определить коэффициент Пуассона по непосредственно измеренным в опыте величинам Р 1 и Р 2.






