 Исходные данные:
Исходные данные:  (рад),
(рад),  (см),
(см), 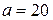 (см),
(см),  см.
см.
Исходное положение механизма изображено на рис.47.
Определить скорость и ускорение точки М в сложном движении при
t =  (c).
(c).
Решение.
|
· первое движение (относительное  ), когда точка М движется в пазу твердого тела D, представляет собой криволинейное движение с кривизной радиуса R;
), когда точка М движется в пазу твердого тела D, представляет собой криволинейное движение с кривизной радиуса R;
· второе движение (переносное  ), когда точка М движется относительно оси z вместе с телом D (вращательное движение относительно оси вращения z).
), когда точка М движется относительно оси z вместе с телом D (вращательное движение относительно оси вращения z).
Для определения абсолютной скорости и ускорения точки М требуется рассмотреть движение точки в заданный момент времени в относительном и переносном движениях.
2.Определим положение системы в заданный момент времени.
2.1. Определим положение точки М в относительном движении.
Для нахождения положения точки в теле D подставим в уравнение  заданный момент времени.
заданный момент времени.
При t = 1/9 с 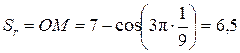 см.
см.
При t = 0 с  см.
см.
Для изображения данного положения на траектории  введем дополнительный угол
введем дополнительный угол  , который образуется относительно центра дуги тела D (радиуса R) между начальным положением точки О и конечным положением М (рис. 48).
, который образуется относительно центра дуги тела D (радиуса R) между начальным положением точки О и конечным положением М (рис. 48).
 рад
рад  .
.
|

2.2. Определим положение точки М в переносном движении.
Для нахождения положения точки, требуется определить положение тела D в заданный момент времени.
При t=1/9 с
 рад
рад 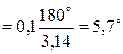
Поскольку для закона вращательного движения относительно оси z ( ) не указано начальное положение, то примем, что система на рис. 48 изображена в заданном положении при
) не указано начальное положение, то примем, что система на рис. 48 изображена в заданном положении при  , а на схеме указано положительное значение
, а на схеме указано положительное значение  .
.
Траекторией точки М в переносном движении является окружность радиусом Re.
3. Определим абсолютную скорость точки М в заданный момент времени.
Абсолютная скорость точки М равна геометрической сумме относительной и переносной скоростей
 .
.
3.1. Определим относительную скорость точки М.
Согласно заданному относительному закону криволинейного движения  скорость определяется как первая производная по времени
скорость определяется как первая производная по времени
 .
.
При t = 1/9 с  см/с.
см/с.
При  > 0, положительное значение относительной скорости в данный момент времени показывает, что вектор скорости
> 0, положительное значение относительной скорости в данный момент времени показывает, что вектор скорости  направлен по касательной к траектории движения
направлен по касательной к траектории движения  из точки М в сторону положительного отсчета по траектории (рис. 49). Положительный отсчет изображается в направлении от точки О к точке М по траектории
из точки М в сторону положительного отсчета по траектории (рис. 49). Положительный отсчет изображается в направлении от точки О к точке М по траектории  .
.
|

3.2. Определим переносную скорость точки М.
Согласно заданному переносному закону вращательного движения  , скорость определяется
, скорость определяется
 ,
,
где Rе – радиус окружности, описываемой точкой М тела D в переносном движении относительно оси z, 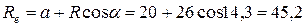 см;
см;
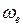 – угловая скорость в переносном движении, определяется как первая производная от закона вращательного движения
– угловая скорость в переносном движении, определяется как первая производная от закона вращательного движения  по времени
по времени
 .
.
При t = 1/9 с
 с-1.
с-1.
Если  > 0, положительное значение
> 0, положительное значение  , показывает, что вращение тела D происходит относительно оси z в сторону, отсчета угла
, показывает, что вращение тела D происходит относительно оси z в сторону, отсчета угла  (
( ).
).
Численное значение вектора скорости в переносном движении составит
 см/с.
см/с.
Вектор  направлен из точки М по касательной к окружности в переносном движении (радиуса Rе) в сторону вращения тела
направлен из точки М по касательной к окружности в переносном движении (радиуса Rе) в сторону вращения тела  (
( //
//  ) (рис.49).
) (рис.49).
3.3.Определим абсолютную скорость точки М.
Поскольку вектора относительной и переносной скоростей взаимно перпендикулярны (принадлежат взаимно перпендикулярным плоскостям, рис.49.), то численное значение абсолютной скорости определим по теореме Пифагора, где  гипотенуза
гипотенуза
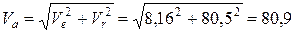 см/с.
см/с.
Вектор абсолютной скорости  графически изобразится из точки М как диагональ построенного параллелограмма на векторах относительной (
графически изобразится из точки М как диагональ построенного параллелограмма на векторах относительной ( ) и переносной (
) и переносной ( ) скоростей.
) скоростей.
4. Определим абсолютное ускорение точки М в заданный момент времени.
Согласно теореме сложения ускорений, абсолютное ускорение точки М в заданный момент времени составит число равное геометрической сумме относительного, переносного и кориолисова ускорений
 .
.
В развернутом виде
 .
.
4.1. Модуль относительного касательного ускорения точки М в заданный момент времени.
 .
.
При t = 1/9 с  см/с2.
см/с2.
Положительное значение  > 0 указывает, что вектор
> 0 указывает, что вектор  направлен по касательной к траектории в относительном движении в сторону положительных значений Sr (рис.50).
направлен по касательной к траектории в относительном движении в сторону положительных значений Sr (рис.50).
Вектора  и
и  направлены в одну сторону, следовательно, относительное движение точки М в данный момент ускоренное.
направлены в одну сторону, следовательно, относительное движение точки М в данный момент ускоренное.
4.2. Относительное нормальное ускорение точки М в заданный момент времени.
 ,
,
где 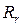 – радиус траектории точки М в относительном движении
– радиус траектории точки М в относительном движении 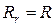
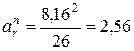 см/с2.
см/с2.
|

Вектор  направлен из точки М к центру кривизны в относительном движении (траектории
направлен из точки М к центру кривизны в относительном движении (траектории  ) (см. рис.50).
) (см. рис.50).
4.3. Модуль переносного касательного ускорения точки М в заданный момент времени
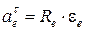 ,
,
где  – угловое ускорение в переносном движении (вращении относительно оси z) тела D.
– угловое ускорение в переносном движении (вращении относительно оси z) тела D.
 .
.
При t = 1/9 с  с-2
с-2
При  >0 положительное значение указывает, что направление углового ускорения
>0 положительное значение указывает, что направление углового ускорения  , совпадает с направлением угла поворота
, совпадает с направлением угла поворота  (
( ).
).
Если направления  и
и  совпадают, то вращение тела D относительно оси z ускоренное (см. рис.50).
совпадают, то вращение тела D относительно оси z ускоренное (см. рис.50).
 см/с2.
см/с2.
Вектор  направлен из точки М перпендикулярно
направлен из точки М перпендикулярно  в сторону, вращения углового ускорения
в сторону, вращения углового ускорения  . Вектора
. Вектора  и
и  направлены в одном направлении при ускоренном движении.
направлены в одном направлении при ускоренном движении.
4.4. Модуль переносного нормального ускорения точки М в заданный момент времени.
 .
.
При t=1/9 с  см/с2.
см/с2.
Вектор  направлен из точки М к центру траектории в переносном движении (к оси вращения z) (см. рис.50).
направлен из точки М к центру траектории в переносном движении (к оси вращения z) (см. рис.50).
4.5. Кориолисово ускорение точки М в заданный момент времени.

Модуль кориолисова ускорения
 ,
,
где  – угол между векторами
– угол между векторами  и
и  , в данном случае
, в данном случае 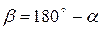 (см. рис.50).
(см. рис.50).
 см/с2.
см/с2.
Вектор 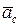 направлен согласно правилу векторного произведения (вектор
направлен согласно правилу векторного произведения (вектор  поворачивают на 90
поворачивают на 90 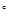 в сторону
в сторону  относительно точки М).
относительно точки М).
4.6. Абсолютное ускорение точки М в заданный момент времени.
Численное значение абсолютного ускорения точки М определим путем проекций векторного равенства ускорений на координатные оси
 .
.
Проецируем векторное равенство ускорений на ось х/
 см/с2.
см/с2.
Проецируем векторное равенство ускорений на ось y/
 ,
,
 см/с2.
см/с2.
Проецируем векторное равенство ускорений на ось z/
 см/с2
см/с2
 см/с2.
см/с2.
Для графического изображения вектора абсолютного ускорения точки
М, строим в масштабе проекции ускорений по координатным осям (рис.51).
|

Приложение
 Образец выполнения титульного листа
Образец выполнения титульного листа
к самостоятельным практическим задачам
 |  |
Федеральное агентство по образованию РФ
Государственное образовательное учреждение
высшего профессионального образования
«Пермский государственный технический университет»
Березниковский филиал
Кафедра технологии и механизации производств






