 Движение твердого тела называется плоскопараллельным или плоским, если все точки этого тела движутся в плоскостях параллельно некоторой неподвижной плоскости.
Движение твердого тела называется плоскопараллельным или плоским, если все точки этого тела движутся в плоскостях параллельно некоторой неподвижной плоскости.
|

|
|
|

При движении плоской фигуры величины хА, уА, j будут изменяться с течением времени, для определения закона движения, надо знать зависимости
 . (62)
. (62)
Уравнения (62) определяют закон движения плоской фигуры и уравнение плоскопараллельного движения твердого тела.
Первые два из уравнений (62) определяют движение, которое совершает фигура при j = const, то есть при поступательном движении, в этом случае все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершает при 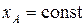 и
и  , в этом случае полюс неподвижен, и происходит вращение фигуры вокруг этого полюса. Следовательно, движение плоской фигуры можно разложить на поступательное, при котором все точки тела движутся так же, как полюс А, и вращательное движение вокруг этого полюса.
, в этом случае полюс неподвижен, и происходит вращение фигуры вокруг этого полюса. Следовательно, движение плоской фигуры можно разложить на поступательное, при котором все точки тела движутся так же, как полюс А, и вращательное движение вокруг этого полюса.
Кинематическими характеристиками плоского движения являются (линейные) скорость и ускорение полюса в поступательном движении ( ,
,  ), а также угловая скорость (w) и угловое ускорение (e) вращательного движения вокруг полюса. С учетом уравнений (62), получим
), а также угловая скорость (w) и угловое ускорение (e) вращательного движения вокруг полюса. С учетом уравнений (62), получим
 ,
,  , (63)
, (63)
 ,
, 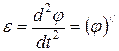 . (64)
. (64)
Поступательное движение зависит от выбора полюса, так как различные точки фигуры имеют разные координаты, а следовательно, и скорости и ускорения.
Вращательное движение от выбора полюса не зависит, угловая скорость и угловое ускорение вращения фигуры вокруг полюса – называется угловой скоростью и угловым ускорением фигуры.






