По заданным уравнениям движения точки М в координатной форме определить: траекторию ее движения в заданный момент времени t= 1c, найти скорость и ускорение.
 (см),
(см), 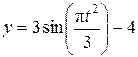 (см).
(см).
Решение:
1. Определим траекторию движущейся точки М.
Для получения уравнения траектории движущейся точки исключим из заданных уравнений параметр времени t:


 ,
,
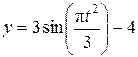

 .
.
Полученные уравнения возведем в квадрат и суммируем.
 ,
,
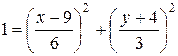 .
.
Данное выражение представляет собой траекторию движущейся точки М – уравнение эллипса с центром в точке с координатами (9; -4). Построим траекторию в координатных осях ху (рис.9).
Укажем положение точки М на траектории в заданный момент времени, для этого подставим время t= 1с в уравнения
 см,
см,
 см.
см.
Тогда точка М с координаты (12; -1,4).
Для указания положительного отсчета по траектории определим положение точки М в начальный момент времени при t= 0 с
 см,
см,
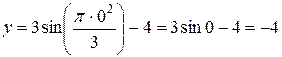 см.
см.
|

Тогда точка Мо имеет координаты (15; - 4).
Точки М и М0 принадлежат траектории эллипса, следовательно, решение верно.
Направление положительного отсчета по траектории идет от точки М0 в момент времени t = 0 c к точке М, когда t =1с (против движения часовой стрелки) (см. рис.9).
2. Определим скорость точки М в заданный момент времени t.
Известно, что скорость можно разложить по проекциям на координатные оси
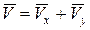 .
.
Определим проекцию скорости точки М на ось Ох
 .
.
В заданный момент времени t =1с проекция скорости составит
 см/с.
см/с.
Так как  < 0, то вектор скорости
< 0, то вектор скорости  направлен из точки М параллельно оси 0х в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе скоростей, указанно на схеме (рис.10).
направлен из точки М параллельно оси 0х в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе скоростей, указанно на схеме (рис.10).
Определим проекцию скорости точки М на ось Оу.
 .
.
В заданный момент времени t =1с проекция скорости составит
 см/с
см/с

|
Так как  >0, то вектор скорости
>0, то вектор скорости  направлен из точки М параллельно оси 0у в сторону положительных значений у, данный вектор требуется отложить в том же масштабе, что и вектор
направлен из точки М параллельно оси 0у в сторону положительных значений у, данный вектор требуется отложить в том же масштабе, что и вектор  (рис.10).
(рис.10).
Геометрическая сумма векторов  и
и  (по правилу параллелограмма) представляет собой вектор скорости
(по правилу параллелограмма) представляет собой вектор скорости  точки М в заданный момент времени, этот вектор должен быть направлен по касательной τ к траектории движения (рис.10). Численное значение скорости
точки М в заданный момент времени, этот вектор должен быть направлен по касательной τ к траектории движения (рис.10). Численное значение скорости  можно измерить, согласно указанному масштабу для векторов скоростей (см. рис.10), либо определить по теореме Пифагора (так как вектора
можно измерить, согласно указанному масштабу для векторов скоростей (см. рис.10), либо определить по теореме Пифагора (так как вектора  и
и  взаимно перпендикулярны):
взаимно перпендикулярны):
 см/с.
см/с.
3. Определим ускорение точки М в заданный момент времени t.
Известно, что ускорение можно разложить по проекциям на координатные оси
 .
.
Определим проекцию ускорения точки М на ось Ох
 .
.
В заданный момент времени t =1с проекция ускорения составит
 см/с2.
см/с2.
Так как  <0, то вектор ускорения
<0, то вектор ускорения  направлен из точки М параллельно оси 0х в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе ускорений, указанно на схеме (рис.11).
направлен из точки М параллельно оси 0х в сторону отрицательных значений х, данный вектор требуется отложить в соответствующем масштабе ускорений, указанно на схеме (рис.11).
Определим ускорение скорости точки М на ось Оу
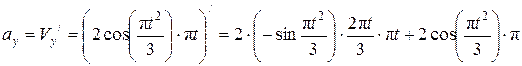 .
.
В заданный момент времени t = 1с проекция ускорения составит
 см/с2.
см/с2.
|

Так как  <0, то вектор ускорения
<0, то вектор ускорения  направлен из точки М параллельно оси 0у в сторону отрицательных значений у, данный вектор требуется отложить в том же масштабе, что и вектор
направлен из точки М параллельно оси 0у в сторону отрицательных значений у, данный вектор требуется отложить в том же масштабе, что и вектор  (рис.11).
(рис.11).
Геометрическая сумма векторов  и
и  (по правилу параллелограмма) представляет собой вектор ускорения
(по правилу параллелограмма) представляет собой вектор ускорения  точки М в заданный момент времени (рис.11). Численное значение ускорения
точки М в заданный момент времени (рис.11). Численное значение ускорения  можно измерить, согласно указанному масштабу для векторов ускорений на схеме чертежа, либо определить по теореме Пифагора (так как вектора
можно измерить, согласно указанному масштабу для векторов ускорений на схеме чертежа, либо определить по теореме Пифагора (так как вектора  и
и  взаимно перпендикулярны):
взаимно перпендикулярны):
 см/с2.
см/с2.
Определим касательное ускорение точки М в заданный момент времени t, зная проекции скорости и ускорения на оси координат
 см/с2.
см/с2.
Так как  > 0, то вектор ускорения
> 0, то вектор ускорения 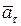 направлен из точки М по касательной к траектории движения в сторону направления вектора скорости
направлен из точки М по касательной к траектории движения в сторону направления вектора скорости  (движение точки будет ускоренным), данный вектор требуется отложить в масштабе ускорений (рис.12).
(движение точки будет ускоренным), данный вектор требуется отложить в масштабе ускорений (рис.12).
Определим нормальное ускорение точки М в заданный момент времени t, зная полное и касательное ускорения
 см/с2.
см/с2.
Вектор ускорения  направлен из точки М по нормали п к траектории движения к центру кривизны траектории, данный вектор требуется отложить в масштабе ускорений (рис.12).
направлен из точки М по нормали п к траектории движения к центру кривизны траектории, данный вектор требуется отложить в масштабе ускорений (рис.12). 
Так как векторная сумма ускорений  справедлива (рис.12), то решение верно.
справедлива (рис.12), то решение верно.
|

Определим радиус кривизны траектории  в заданный момент времени c учетом нормального (центростремительного) ускорения в заданный момент времени
в заданный момент времени c учетом нормального (центростремительного) ускорения в заданный момент времени
 см.
см.






