 Вращательным движением твердого тела называется движение, при котором две точки тела остаются неподвижными (точки А и В, рис.15). Прямая, проходящая через неподвижные точки, называется осью вращения (ось Az). Точки, не лежащие на оси вращения, описывают окружности по отношению к оси вращения. Плоскости этих окружностей перпендикулярны оси вращения, а их центры лежат на оси вращения.
Вращательным движением твердого тела называется движение, при котором две точки тела остаются неподвижными (точки А и В, рис.15). Прямая, проходящая через неподвижные точки, называется осью вращения (ось Az). Точки, не лежащие на оси вращения, описывают окружности по отношению к оси вращения. Плоскости этих окружностей перпендикулярны оси вращения, а их центры лежат на оси вращения.
|
При вращении тела угол j изменяется с течением времени по определенному закону в зависимости от характера вращательного движения
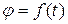 . (38)
. (38)
Уравнение (38) называется законом вращательного движения тела относительно неподвижной оси.
В случае, если известно число оборотов совершаемого тела N в некоторую единицу времени, угол поворота тела составит
 . (39)
. (39)
Для характеристики изменения вращения тела вокруг оси вводится понятие угловой скорости тела  . Единицы измерения угловой скорости – рад/с или с-1.
. Единицы измерения угловой скорости – рад/с или с-1.
Пусть за промежуток времени  тело совершает поворот на угол
тело совершает поворот на угол 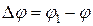 , тогда средней угловой скоростью тела будет отношение
, тогда средней угловой скоростью тела будет отношение
 . (40)
. (40)
Угловой скоростью в данный момент времени, называется предел отношения уравнения (40), при стремлении времени  , то есть
, то есть
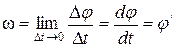 . (41)
. (41)
Угловая скорость вращения тела в данный момент времени равна первой производной от угла поворота тела по времени.
Положительным направлением вращения угловой скорости в данный момент времени считается вращение против часовой стрелки, если смотреть с положительного направления оси Az (см. рис.15).
Если тело вращается неравномерно, то для характеристики быстроты изменения угловой скорости вводится понятие углового ускорения  . Единицы измерения углового ускорения – рад/с2 или с-2.
. Единицы измерения углового ускорения – рад/с2 или с-2.
Пусть за время  угловая скорость изменилась на
угловая скорость изменилась на  , тогда значение среднего углового ускорения составит
, тогда значение среднего углового ускорения составит
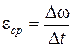 . (42)
. (42)
Угловое ускорение в данный момент времени называется пределом отношения уравнения (42), при стремлении времени  , то есть
, то есть
 . (43)
. (43)
Угловое ускорение в данный момент времени представляет собой первую производную от угловой скорости или вторую производную от угла поворота тела по времени.
Движение тела (точки) будет ускоренным, если численные значения угловой скорости ( ) и углового ускорения (
) и углового ускорения ( ) в данный момент времени имеют одинаковые знаки (рис.16,а), и замедленным, когда разные (рис.16,б).
) в данный момент времени имеют одинаковые знаки (рис.16,а), и замедленным, когда разные (рис.16,б).
|
|
|
 Угловую скорость, как и угловое ускорение тела можно изобразить в виде векторов
Угловую скорость, как и угловое ускорение тела можно изобразить в виде векторов  и
и  , численные значения которых равны
, численные значения которых равны  и
и  , соответственно. Вектор угловой скорости и углового ускорения требуется изображать вдоль оси вращения тела в сторону, откуда вращение происходит против хода часовой стрелки (рис.16). Задав вектора угловой скорости и углового ускорения, определяют численные значения их модулей, положение оси вращения и направление вращения вокруг этой оси.
, соответственно. Вектор угловой скорости и углового ускорения требуется изображать вдоль оси вращения тела в сторону, откуда вращение происходит против хода часовой стрелки (рис.16). Задав вектора угловой скорости и углового ускорения, определяют численные значения их модулей, положение оси вращения и направление вращения вокруг этой оси.
Если угловая скорость тела остается во время движения постоянной ( ), то вращение тела называется равномерным. Интегрируя уравнение (41) в заданных пределах, имеем
), то вращение тела называется равномерным. Интегрируя уравнение (41) в заданных пределах, имеем
 , (44)
, (44)
 ,
,
где 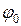 - угол поворота тела в момент времени t =0;
- угол поворота тела в момент времени t =0;
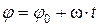 . (45)
. (45)
Выражение (45) отображает закон равномерного вращательного движения твердого тела.
Если угловое ускорение тела во время движения остается постоянным ( ), то вращение называется равнопеременным. Интегрируя выражение (43) в заданных пределах, имеем
), то вращение называется равнопеременным. Интегрируя выражение (43) в заданных пределах, имеем
 , (46)
, (46)
 ,
,
где  - угловая скорость тела в момент времени t = 0.
- угловая скорость тела в момент времени t = 0.
С учетом выражения (41) получим
 . (47)
. (47)
Интегрируя выражения в заданных пределах
 , (48)
, (48)
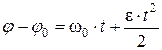 ,
,
 . (49)
. (49)
Выражение (49) определяет закон движения при равнопеременном вращении.
Если модуль угловой скорости с течением времени увеличивается, то движение – равноускоренное, если уменьшается – равнозамедленное.
Уравнения для равноускоренного движения:
 ,
,  .
.
В случае, равнозамедленного движения:
 ,
,  .
.






