Определим численное значение

.

Угол требуется отложить из точки А от вектора ускорения в сторону , проводим из точки А луч АК (см. рис.36).

Численное значение отрезка AQ составит

см.

Откладываем отрезок AQ на линии луча АК в масштабе построенной схемы.

Точка Q представляет собой МЦУ звена АВ.

5.2.2. Определим ускорение точки В ().

Поскольку ускорение точки В определяется как вращательное относительно МЦУ звена АВ (точка Q), то численное значение ускорения составит (отрезок замеряем в масштабе построенной схемы, см)

Для графического изображения вектора в точке В (см. рис.36) необходимо от отрезка отложить угол (который изображается с той же стороны, что и для точки А с отрезком ) в направлении полученного луча из точки В направлен вектор ускорения точки .

5.2.3. Определим ускорение точки М ().

Рис.36.

Поскольку точка М принадлежит звену АВ, при этом определено положение МЦУ звена АВ (точки Q). Численное значение ускорения составит ( равен 70,52 см)

см/с².

Для графического изображения вектора в точке М (см. рис.36) необходимо от отрезка отложить угол (который изображается с той же стороны, что и для точки А с отрезком ), в направлении полученного луча из точки M направлен вектор ускорения точки .

6. Проверка допустимости приведенных расчетов ускорений многозвенного механизма методами плана и МЦУ

Таблица 4.

Сравниваемая величина	По методу плана	По методу МЦУ	Процент расхождения,
аB	72,9	75,6	3,6%
аМ		105,8	1,7%

 

Если расхождение сравниваемых величин не превышает 5%, то приведенное решение считается верным.

 

 

Практическая работа 3

Определение скорости и ускорения точек плоского механизма.

Исходные данные: с^-1, с^-2, см, см,

Рис. 37.

Определить скорости и ускорения точек А, В и угловую скорость и угловое ускорение вращения колеса (рис. 37).

Решение.

1. Определим скорости точек А и В плоского механизма, угловой скорости колеса.

1.1. Определим скорость точки А.

Точка А принадлежит звену АО, совершающего вращательное движение относительно неподвижной точки О. Численное значение скорости точки А определим по формуле

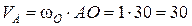см/с.

Вектор скорости точки А направлен перпендикулярно радиусу АО в сторону вращения угловой скорости (рис.38).

1.2.Определим угловую скорость колеса (диска).

Мгновенный центр скоростей (МЦС) диска точка Р расположен в точке соприкосновения колеса с неподвижной поверхностью, по которой перекатывается колесо (рис.38).

Под действием вектора скорости точки А колесо приобретает угловую скорость () относительно неподвижной точки Р, направленную против часовой стрелки (рис.38). Численное значение угловой скорости колеса составит

,

где – радиус вращения точки А относительно МЦС колеса точки Р, РА=АВ,

Рис. 38.

с^-1.

1.3.Определим скорость точки В.

Точка В принадлежит колесу, которое совершает вращательное движение относительно МЦС, точки Р. Скорость точки В составит

,

где – радиус вращения точки В относительно МЦС колеса точки Р, для нахождения данного отрезка рассмотрим вспомогательный треугольник ВАР (рис. 39).

Рис.39.

В равностороннем треугольнике ВАР (АВ=АР) угол ВАР равен (90- ), тогда в прямоугольном треугольнике ВСА угол ВАС будет равен , так как АС является биссектрисой угла ВАР.

Определим ВС см.

Так как треугольники ВСА и САР подобны, то ВР = 2 ВС = 20 см

см/с.

Вектор скорости точки В () направлен перпендикулярно ВР в сторону вращения угловой скорости (рис.38).

2. Определим ускорения точек А, В и угловое ускорение колеса.

2.1. Определим ускорение точки А.

Точка А принадлежит звену АО, совершающему вращательное движение относительно неподвижной точки О, тогда вектор ускорения точки равен векторной сумме вектора нормального (центростремительного) и касательного (вращательного) ускорений

,

где – вектор нормального ускорения точки А на звене АО;

– вектор касательного ускорения точки А на звене АО.

Численное значение нормального ускорения точки А составит

см/с².

Вектор направлен из точки А, к центру вращения точке О.

Численное значение касательного ускорения точки А составит

см/с².

Вектор направлен из точки А перпендикулярно АО в сторону вращения углового ускорения (рис. 40).

Векторная сумма векторов и даст графическое изображение вектора ускорения точки А.

Рис. 40.

Поскольку и взаимно перпендикулярны, то численное значение ускорения точки А определится по теореме Пифагора

см/с².

2.2. Определим угловое ускорение колеса.

Поскольку угловая скорость колеса равна , где РА =constи ОА =const, то угловое ускорение колеса будет равно

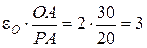с^-2.

Так как в данный момент времени угловая скорость и угловое ускорение звена ОА соноправлены (движение ускоренное), то и колесо будет находиться в ускоренном движении .

2.3. Определим ускорение точки В.

Для нахождения ускорения точки В примем за полюс ускорение точки А, тогда составим векторное уравнение ускорений

,

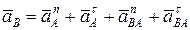где – вектор нормального ускорения точки В относительно полюса точки А;

– вектор касательного ускорения точки В относительно полюса точки А.

Численное значение нормального ускорения составит

см/с².

Вектор направлен из точки В к центру вращения точки А (см. рис. 40).

Численное значение касательного ускорения составит

см/с².

Вектор направлен из точки А перпендикулярно АВ в сторону вращения углового ускорения (см. рис. 40).

Поскольку известны все составляющие векторного равенства (правой части уравнения), как по модулю, так и по направлению, то определим ускорение точки В путем проекций на координатные оси х и у векторного равенства ускорений.

Ускорение точки В в проекции на ось х

,

см/с2   44444141.

Рис. 41 44444141.

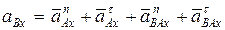Ускорение точки В в проекции на ось у

,

см/с².

Численное значение ускорения точки В составит

см/с².

Для изображения вектора ускорения точки В сложим геометрически составляющие векторного равенства в правой части и укажем на схеме механизма в соответствующем масштабе (рис. 41).

 

Сложное движение точки

3.7.1. Абсолютное, относительное и переносное движение точки

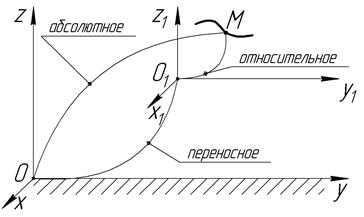В ряде случаев возникает необходимость рассматривать движение точек одновременно по отношению к двум системам отсчета, одна из которых принимается за неподвижную, а вторая определенным обра-зом движется по отношению к первой. Движение точки в этом случае называется сложным.

Рис. 42.

Рассмотрим движение точки М по отношению к некоторой системе отсчета О₁х₁у₁z₁, которая в свою очередь сама движется по отношению к системе отсчета Охуz, принимаемую за неподвижную (рис. 42). Движение точки М по отношению к подвижной системе отсчета О₁х₁у₁z₁, называется относительным. Траектория, скорость и ускорение в этом движении называются относительной траекторией (), относительной скоростью (), относительным ускорением ().

Движение подвижной системы отсчета О₁х₁у₁z₁ по отношению к неподвижной системе отсчета Охуz, называется переносным. Траектория, скорость, ускорение точки М в подвижной системе отсчета О₁х₁у₁z₁ относительно неподвижной Охуz, называется переносной траекторией (), переносной скоростью (), переносным ускорением ().

Движение точки М по отношению к неподвижной системе отсчета, называется абсолютным. Траектория, скорость и ускорение в этом движении называется абсолютной траекторией (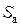), абсолютной скоростью (), абсолютным ускорением ().

Абсолютное движение точки М является сложным и состоит из относительного и переносного движений.