КИНЕМАТИКА
Методическое пособие к выполнению самостоятельных практических работ
по дисциплине «Теоретическая механика»
Березники 2008
Составитель: С.М. Вдовин
УДК 531.5
ББК 22.21
В25
Рецензент: канд. техн. наук, доцент кафедры технологии и механизации производств БФ ПГТУ С.Э. Шаклеина
Кинематика: метод. пособие / С.М. Вдовин.– Перм. гос. техн. ун-т. Березники, 2008. – 67с.
Представлены базовые теоретические сведения по кинематике точки и твердого тела, рассмотрены основные задачи. Данное пособие предназначено для самостоятельной подготовки студентов технических вузов всех специальностей дневного, вечернего и заочного отделений к практическим занятиям по разделу кинематика, дисциплины «Теоретическая механика».
УДК 531.5
Ó «Пермский государственный
технический университет», 2008
Содержание
1. Введение в кинематику................................................................................ 4
2. Кинематика точки........................................................................................ 4
2.1. Скорость точки..................................................................................... 5
2.2. Определение скорости при координатном способе задания движения точки 6
2.3. Определение скорости при естественном способе задания движения точки 7
2.4. Ускорение точки.................................................................................... 7
2.5. Определение ускорения точки при координатном способе задания движения точки...................................................................................................................... 8
2.6. Касательное и нормальное ускорение точки....................................... 9
2.7. Касательное и нормальное ускорения при координатном способе задания движения точки........................................................................................................... 10
2.8. Частные случаи движения точки........................................................ 11
Практическая работа 1.............................................................................. 12
3. Кинематика абсолютно твердого тела..................................................... 17
3.1. Поступательное движение.................................................................. 17
3.2. Вращательное движение тела............................................................. 18
3.3. Скорости и ускорения точек тела при вращательном движении..... 22
3.4. Плоскопараллельное движение твердого тела.................................. 24
3.5. Определение скоростей точек тела плоской фигуры........................ 26
3.5.1. Метод полюса............................................................................... 26
3.5.2. Метод мгновенного центра скоростей (МЦС)............................. 27
3.5.2.1. Понятие о центроидах............................................................... 28
3.5.2.2. Частные случаи МЦС................................................................ 28
3.6. Определение ускорений точек тела плоской фигуры........................ 29
3.6.1. Метод полюса............................................................................... 29
3.6.2. Метод мгновенного центра ускорений (МЦУ)............................ 30
Практическая работа 2.............................................................................. 32
Практическая работа 3.............................................................................. 48
3.7. Сложное движение точки.................................................................... 52
3.7.1. Абсолютное, относительное и переносное движение точки....... 52
3.7.2. Теорема сложения скоростей....................................................... 52
3.7.3. Теорема о сложении ускорений................................................... 54
Практическая работа 4.............................................................................. 58
Приложение................................................................................................... 65
Список используемой литературы............................................................... 66
Введение в кинематику
Кинематика – раздел теоретической механики, в котором изучаются пространственно-временные свойства движения различных объектов с геометрической точки зрения, с целью расчета траекторий, скоростей и ускорений отдельных точек (изолированных), так и входящих в состав абсолютно твердого тела. Владение данными умениями полезно при разработке реальных механических систем, выявлении структуры их виртуальных перемещений, составлении уравнений динамики.
Движение представляет собой изменение положения тела с течением времени в пространстве относительно других материальных тел. Для определения данного положения движущейся точки (тела) в различные моменты времени вводят систему отсчета, жестко связанную с некоторым телом. Система отчета представляет собой систему трех координатных осей, в которой перемещается исследуемый объект.
Изучение кинематики рассматривается с движения простейшего объекта – точки.
Кинематика точки
Движение точки можно задать одним из следующих способов:
1. Векторный способ задания движения точки.
 Рассматривается движение точки М в некоторой системе отчета Охуz. Положение этой точки в любой момент времени определяют радиус-вектором
Рассматривается движение точки М в некоторой системе отчета Охуz. Положение этой точки в любой момент времени определяют радиус-вектором 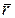 , проведенным из начала координат точки О к точке М (рис.1).
, проведенным из начала координат точки О к точке М (рис.1).
|
|
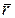 изменяется с течением времени по модулю и направлению, следовательно
изменяется с течением времени по модулю и направлению, следовательно
 (1)
(1)
где  – векторная функция, изменяется с течением времени.
– векторная функция, изменяется с течением времени.
Равенство (1) определяет закон движения точки в векторной форме, позволяет найти ее положение в любой момент времени.
При проектировании радиус-вектора 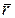 на декартовы координаты и введении единичных векторов
на декартовы координаты и введении единичных векторов  координатных осей имеем
координатных осей имеем
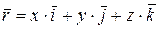 , (2)
, (2)
где х, у, z – декартовы координаты точки М.
Вектор 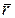 согласно равенства (1) может быть задан модулем и углами с осями или проекциями на оси других систем координат.
согласно равенства (1) может быть задан модулем и углами с осями или проекциями на оси других систем координат.
2. Координатный способ задания движения точки.
Рассматривается движение точки М в некоторой системе отсчета. Положение этой точки в любой момент времени определяют декартовыми координатами х, у, z.
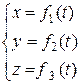 . (3)
. (3)
Уравнение (3) называется уравнением движения точки в прямоугольных декартовых координатах.
При движении точки в одной плоскости Оху уравнение движения примет вид
 . (4)
. (4)
При прямолинейном движении точки, вдоль оси Ох уравнение движения примет вид
 . (5)
. (5)
Равенство (5) выражает прямолинейный закон движения точки.
Выражения (3) и (4) представляют уравнения траектории точки в параметрической форме, зависящие от параметра времени t.
Траектория представляет собой непрерывную линию, которую описывает материальная точка по отношению к данной системе отсчета. Для выявления уравнения траектории точки требуется исключить параметр времени из заданных уравнений.
3. Естественный способ задания движения точки.
 В некоторой системе декартовых координат Оxyz, задается движение точки М (рис.2), при этом известны:
В некоторой системе декартовых координат Оxyz, задается движение точки М (рис.2), при этом известны:
· траектория АВ, по которой движется точка М;
· начальное положение точки на траектории – точка О1, указание положительного и отрицательного отсчета направлений движения;
·
|
S=f(t). (6)
Уравнение (6) выражает закон движения точки М по траектории.
Скорость точки
Скорость точки – одна из основных кинематических характеристик, является векторной величиной и характеризует быстроту изменения положения точки.
Пусть в некоторый момент времени t движущаяся точка находится в положении М и определяется радиусом-вектором 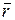 , а в момент t1 приходит в положение М1, определяется вектором
, а в момент t1 приходит в положение М1, определяется вектором  (рис.3).
(рис.3).
За промежуток времени 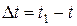 точка М, совершит перемещение по кривой ММ1, определяющееся вектором
точка М, совершит перемещение по кривой ММ1, определяющееся вектором  .
.
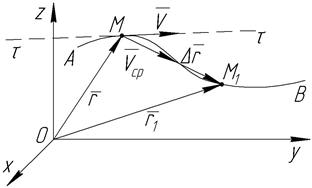 Вектор
Вектор  называется вектором перемещения точки за промежуток времени
называется вектором перемещения точки за промежуток времени 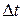 .
.
|
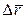 к соответствующему промежутку времени
к соответствующему промежутку времени 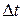 :
:
 . (7)
. (7)
Вектор 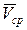 совпадает с направлением вектора
совпадает с направлением вектора  .
.
Скорость точки в данный момент времени  называется вектор
называется вектор  численно равный пределу отношения вектора перемещения точки
численно равный пределу отношения вектора перемещения точки  к промежутку времени
к промежутку времени 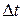 , при
, при  .
.
 или
или  . (8)
. (8)
Следовательно, вектор скорости в данный момент времени есть первая производная по времени от радиуса-вектора движущейся точки 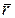 .
.
Вектор скорости в данный момент времени  направлен по касательной к траектории точки
направлен по касательной к траектории точки  в сторону ее движения (рис.3).
в сторону ее движения (рис.3).
Определение скорости при координатном способе задания движения точки
На основании выражений (8) и (2)
 . (9)
. (9)
 В свою очередь вектор скорости, в заданный момент времени, также можно представить через проекции скоростей на единичные вектора координатных осей,
В свою очередь вектор скорости, в заданный момент времени, также можно представить через проекции скоростей на единичные вектора координатных осей,
 . (10)
. (10)
|
 ,
,  ,
,  . (11)
. (11)
Таким образом, проекции скорости точки на координатные оси представляют собой первые производные от соответствующих координат движущейся точки по времени.
Зная проекции вектора скорости на оси координат, определим модуль скорости и косинусы углов с осями координат (рис.4)
 , (12)
, (12)


 . (13)
. (13)




