ЕРС, що утворюються в трьохфазному генераторі будуть однакові за амплітудним значенням і частоті, але зсунуті за фазою відносно одна одної на 1/3 періоду. Виводи початків обмоток трифазного генератора прийнято позначати буквами А, В, С. Маркіровка виводів виконується з таким розрахунком, щоб індуковані в обмотках ЕРС ` E A, ` E B, ` E C відставали на третину періоду ` E B від ` E A, ` E C від` E B.
Беручи за початок відліку момент часу, коли ЕРС е А в обмотці А дорівнює нулю і змінює свої значення з від’ємних на додатні, можна записати такі вирази:
е А = Е m sinw t;
е B = Е m sin (w t – 120°);
е C = Е m sin (w t – 240°) = Е m sin (w t + 120°).
Графіки цих ЕРС мають вид:
При символічній формі запису, якщо ЕРС фази А дорівнює 
, то ЕРС фаз В і С відповідно складають:
Векторна діаграма для амплітудних значень ЕРС 
буде уявляти собою симетричну трипроменеву зірку. Для такої системи справедливе співвідношення 
. Таке ж співвідношення справедливе і для діючих значень 
.
Дійсно, з діаграми видно, що геометрична сума трьох векторів, рівних за величиною і зсунутих за фазою на третину періоду (120°) дорівнює нулю. Сума миттєвих значень ЕРС трифазного генератора в будь–який момент часу також дорівнює нулю е А + е В + е С = 0.
Якщо об’єднати кінці обмоток генератора в спільну точку О, а кінцеві зажими навантажень в спільну точку О¢, то для з’єднання генератора і трьох навантажень потрібно буде чотири проводи.
Точки О, О’ називають відповідно нульовою (або нейтральною) точкою генератора і нульовою (нейтральною) точкою навантаження.
Проводи А–А, В–В, С–С називають лінійними, а провод О–О’ – нульовим або нейтральним. Отримана схема має назву чотирипроводна система трифазного струму, або з’єднання зіркою з нульовим проводом.
Напруга між лінійним проводом і нульовим має назву фазна напруга і позначається U A, U B, U C.
Напруга між лінійними проводами називається лінійною напругою і позначається U AВ, U BС, U СА.
До навантажень Z A, Z B, Z C прикладені фазні напруги.
В трифазних колах розрізняють лінійні І л і фазні І Ф струми.
Лінійними називають струми І А, І В, І С, щопротікають по лінійних проводах.
Струми, що протікають по обмотках генератора, або по опорах навантаження називають фазними.
При з’єднанні зіркою лінійний струм рівний фазному І л = І Ф.
Струм, що протікає по нульовому проводі, позначають І N.
Для чотирипроводної системи:
Застосувавши до нульової точки О’ перший закон Кірхгофа і прийнявши позначені на схемі додатні напрямки струмів отримаємо:
або
тобто струм в нульовому проводі визначається сумуванням лінійних струмів в комплексній формі, або геометричним сумуванням векторів ` І А, ` І В, ` І С.
На малюнку стрілками показані додатні напрямки фазних напруг на опорах навантаження. Миттєва напруга, наприклад напруга u AB, між лінійними проводами А і В дорівнює алгебраїчній сумі миттєвих напруг на дільниці кола між точками А і В: u AB = u A + (– u B)
В цьому виразі напругу u B взято із знаком “–“ оскільки напрям дії цієї напруги протилежний прийнятому напряму обходу кола від точки А до точки В.
Теж саме в діючих значеннях:
.
Аналогічно для лінійних напруг: 
і 
:
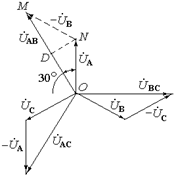
Векторна діаграма напруг матиме вид:
З діаграми видно, що всі три лінійні напруги рівні між собою за величиною і зсунуті по фазі відносно одна одної на 120°.
З трикутника OMN маємо:
OM = 2×OD = 2×ON×cos 30° = 
×ON.
Оскільки ОМ = U AB = U л; ON = U A = U Ф, то U л =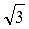 
× U Ф, тобто лінійна напруга при з’єднанні зіркою в 
разів більша за фазну.
В трифазних установках навантаження окремих фаз прагнуть зробити більш-менш однаковим. При цьому струм в нульовому проводі виявляється меншим кожного з лінійних струмів. Виходячи з цього перетин нульового проводу приймають рівним приблизно половині перетину лінійного проводу.
Потужність трифазного кола при з’єднанні зіркою. Активні і реактивні потужності в кожній з фаз трифазної системи можна знайти за формулами:
P A = U A I Acos j A P B = U B I Bcos j B P C = U C I Ccos j C
Q A = U A I Asin j A Q B = U B I Bsin j B Q C = U C I Csin j C
Загальна потужність трифазної системи (активна і реактивна) визначається сумою потужностей окремих фаз: P = P A + P B + P C; Q = Q A + Q B + Q C.
При симетричному навантаженні: P A = P B = P C = P ф; Q A = Q B = Q C = Q ф; j A = j B = j C = j. Тоді:
P = 3× P ф = 3× U ф I фcos j; Q = 3× Q ф = 3× U ф I фsin j; S = 3× U ф I ф.
Ці формули визначають потужність трифазної системи через фазні струми і напруги.
Іноді буває зручніше вираховувати потужність через лінійні величини струмів і напруг. Враховуючи, що при з’єднанні зіркою І л = І Ф і U л = × U Ф, отримаємо
P = × U л I лcos j
Q = 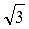× U л I лsin j
S = 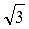× U л I л
Трипровідна система. При симетричному (рівномірному) навантаженні фаз, тобто, коли опори навантажень однакові Z A = Z B = Z C вектори струмів в усіх фазах рівні за величиною і зсунуті відносно своїх напруг на один і той же кут j.
Векторна діаграма в цьому випадку має вид:
Сума лінійних струмів дорівнює нулю, а отже струм в нульовому проводі відсутній (І N = 0).
При симетричному навантаженні відпадає необхідність в нульовому проводі і передачу енергії від генератора до споживачів можна здійснювати по трьом проводам.
Схема трипровідної передачі має вид, наведений нижче.
Електричні мережі виконуються трипровідними тільки для живлення таких споживачів, кожний з яких створює симетричне навантаження всіх трьох фаз.
Напруги між лінійними проводами практично залишається рівними за величиною (U AВ = U BС = U СА) і взаємно зсунуті по фазі на 120° як при симетричному так і при несиметричному навантаженні фаз. Фазні ж напруги в трипровідній мережі однакові за величиною тільки у випадку симетричного навантаження фаз.
Якщо в цій мережі через будь-які обставини порушується рівномірність навантаження окремих фаз, то напруга між нульовою точкою навантаження і лінійними проводами, тобто фазні напруги споживачів U A, U B, U C будуть неоднакові. У зв’язку з цим встановлене раніше співвідношення U л =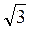 
× U Ф для трипровідної системи справедливе тільки при симетричному навантаженні фаз.
При симетричному навантаженні фаз (Z A = Z B = Z C = Z) розрахунок трифазного кола зводиться до розрахунку однофазного кола.
За заданим U л визначають фазну напругу U ф = U л / 
, а потім за відомим опором навантаження Z визначають струм в проводах живлення 
. Зсув фаз між струмом і фазною напругою визначають за формулою cosj = R / Z.
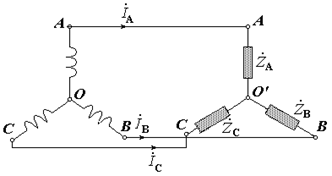
Методика розрахунку з використанням комплексних чисел. При значній нерівномірності навантаження окремих фаз і особливо при відсутності нульового проводу симетрія напруг у споживачів порушується. В таких випадках, коли розрахунок трифазної системи не можна звести до розрахунку кіл окремих фаз з однаковими за величиною напругами, використовують символічний метод. Розглянемо схему чотирипровідної системи з урахуванням опорів проводів:
Чотирипровідну систему можна розглядати як складне коло з двома вузлами О і О’ і для розрахунку застосувати метод вузлових напруг.
Позначимо:
– фазні напруги на клемах генератора;
– фазні напруги на клемах навантаження;
– повні опори окремих фаз, включаючи опори лінійних проводів;
– повні провідності окремих фаз;
– опір нульового проводу;
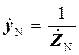– провідність нульового проводу.
Вважаємо, що вузловий потенціал в вузлі О дорівнює нулю. Тоді рівняння для вузла О', складене за методом вузлових напруг буде мати вид:
Вузлова напруга, тобто напруга між нульовою точкою навантаження О’ і нульовою точкою генератора О, визначається за формулою:
Далі, за методом вузлових напруг визначаються струми в вітках, тобто струми в нульовому і лінійних проводах:
Напруги на опорах навантаження:
Нехтуючи опором лінійних проводів за попередніми формулами отримуємо співвідношення між фазними напругами генератора і навантаження:
Нагадуємо, що при симетричному навантаженні напруга U N між нульовими точками генератора і навантаження дорівнює нулю, оскільки діючі напруги U А, U В, U С на клемах навантаження рівні за величиною і зсунуті по фазі на третину періоду.
Приклад. В 4–провідну мережу 3–фазного струму з лінійною напругою U л = 220 в включені зіркою три групи ламп з опором R А = 10 Ом, R В= 5 Ом, R С = 7,5 Ом. Визначити фактичні напруги на клемах ламп, що включені в фази А, В, С при обриві нульового проводу.
Розв’язання:
Оскільки опір лінійних проводів малий в порівнянні з опором ламп, можна вважати Z A » R А = 10 Ом; Z B » R В= 5 Ом; Z С » R С = 7,5 Ом.
Нехай вектор 
спрямований по дійсній осі. Тоді для фазних напруг джерела можна записати:
провідність окремих фаз:
При відсутності нульового проводу 
.
Напруга між точками О і О’:
Фазні напруги на клемах навантаження:
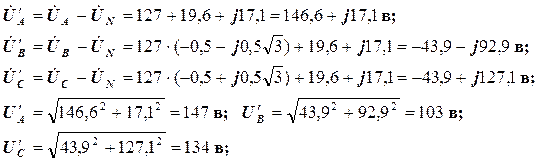
Напруги U A ' і U В ' на менш завантажених фазах перевищують номінальну напругу ламп, тому лампи, включені в фази А і С, можуть швидко перегоріти.
Векторна діаграма має вид:
Вихідна точка О відповідає нульовій точці генератора, а кінці векторів 
– точкам А, В, С кола. Від точки О відкладаємо вектор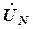 
, кінець якого О' відповідає нульовій точці О' навантаження. Відрізки, що з’єднують на діаграмі точку О' з кінцями векторів 
уявляють собою вектори напруг 
. Вектори 
зображують лінійні напруги кола.
При симетричному навантаженні точка О' співпадає на діаграмі з початком векторів О. При порушенні симетрії навантаження точка О' зміщується відносно початку векторів О. Це явище має назву зміщення нейтралі.
Опір нульового проводу, як правило в багато разів менше опору навантаження будь–якої з фаз, тобто провідність нульового проводу y N значно перевищує провідність окремих фаз y А, y В, y С. Це означає, що при наявності нульового проводу величина 
зменшується в кілька разів, і фазні напруги 
в цих умовах утворюють трифазну систему, достатньо близьку до симетричної.
З’єднання споживачів за схемою “трикутник”. Якщо в мережу трифазного струму між кожною парою лінійних проводів А–В, В–С, С–А включити три опори Z AB, Z BC, Z CA, то під дією лінійних напруг в кожному з цих опорів буде протікати струм. Такий спосіб включення навантажень в трифазну мережу має назву включення трикутником.
При з’єднанні навантажень “трикутником” по їх опорам протікають струми I AB, I ВC, I CA. Ці струми називають фазними. Струми I A, I В, I C, що протікають в лінійних проводах мережі називають лінійними. Показані на малюнку напрямки струмів є загальноприйнятими позитивними напрямками.
Напруга, що прикладена до опорів навантажень Z AB, Z BC, Z CA прийнято називати фазними напругами U ф. В наведеній схемі фазна напруга дорівнює напрузі між лінійними проводами, тобто лінійній напрузі U л. Тому при з’єднанні “трикутником” U л = U ф .
Вибір схеми з’єднання споживачів вирішується в залежності від величини лінійної напруги мережі і номінальної напруги споживачів. В трифазних установках можливі випадки, коли одна частина споживачів з’єднана “зіркою”, а інша – “трикутником”.
З’єднання обмоток генератора за схемою “трикутник”. З’єднання “трикутником” – це коли початок кожної фазної обмотки з’єднується з кінцем наступної по порядку фазної обмотки так, що всі три обмотки утворюють замкнутий контур. В цьому контурі напрямки фазних ЕРС е АВ, е ВС, е СА співпадають.
До клем А, В, С приєднується трифазна мережа, що живить навантаження. Лінійні напруги між кожною парою клем дорівнює фазній напрузі джерела (U л = U ф).
При відсутності навантаження струм в контурі генератора АВСА не виникає, оскільки результуюча (сумарна) ЕРС в контурі в будь–який момент часу дорівнює нулю (е АВ + е ВС + е СА = 0).
Звичайно, обмотки електромашинних генераторів з’єднують зіркою. Обмотки трифазних трансформаторів, від яких живляться споживачі, прийнято з’єднувати як “зіркою”, так і “трикутником”.
Фазні і лінійні струми при з’єднанні “трикутником”. При заданій величині лінійної напруги U л = U ф, відомих значеннях опорів навантаження можна розрахувати фазні струми і коефіцієнти потужності окремих фаз:
Для встановлення співвідношень між лінійними і фазними струмами складаються рівняння за першим законом Кірхгофа для точок розгалуження А, В, С, враховуючи вибрані додатні напрямки струмів:
Звідки
З отриманих виразів випливає, що кожний вектор лінійного струму дорівнює різниці векторів відповідних фазних струмів.
Векторна діаграма напруг 
, фазних струмів 
і лінійних струмів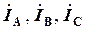 
має вид:
Складаючи праві і ліві частини рівнянь (1) отримаємо 
, тобто сума лінійних струмів дорівнює нулю як при симетричному, так і при несиметричному навантаженні.
При симетричному навантаженні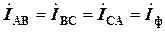 
; j AB = j BC = j CA = j.
В цьому випадку лінійні струми рівні між собою 
і утворюють правильну трипроменеву зірку. Із рівнобедреного трикутника OMN можна знайти співвідношення між величинами лінійного і фазного струмів. При симетричному навантаженні 
.
Потужність трифазного кола при з’єднанні навантажень “трикутником”. В цьому випадку потужність визначається за тими же формулами, що і при з’єднані “зіркою”.
Потужність окремих фаз:
P AB = U AB × I AB × cos j AB;
Q AB = U AB × I AB × sin j AB;
P BC = U BC × I BC × cos j BC;
Q BC = U BC × I BC × sin j BC;
P CA = U CA × I CA × cos j CA;
Q CA = U CA × I CA × sin j CA.
Загальна потужність трифазної системи визначається сумою потужностей окремих фаз
Р = P AB + P BC + P CA
Q = Q AB + Q BC + Q CA
При симетричному навантаженні потужності окремих фаз рівні між собою, отже
Р = 3× Р ф = 3× U ф ×I ф × cos j; Q = 3× Q ф = 3× U ф ×I ф × sin j; S = 3× U ф ×I ф
Враховуючи, що при з’єднанні “трикутником” U л = U ф і 
, можна отримати вирази потужностей через величини лінійних струму і напруги:
Р = × U л ×I л × cos j
Q = × U л ×I л × sin j
S = 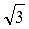× U л ×I л
На практиці буває необхідно переключити опори навантаження із схеми “трикутник” на схему “зірка”, наприклад, переключення трифазних електропечей з метою регулювання їх потужності, а, відповідно і температури. Потужність, що споживається при з’єднанні “трикутником”, буде при тій же напрузі мережі в тричі більшою за потужність, що споживається цими ж опорами при з’єднанні “зіркою”. Дійсно, при з’єднанні “зіркою”
,
а при з’єднанні “трикутником”
,
звідки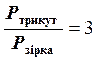 
.
Приклад 1. До трифазної мережі із лінійною напругою U л= 220 В підключене симетричне навантаження, з’єднане за схемою «трикутник». Активний опір фази R ф = 4 Ом, реактивний індуктивний – Х ф = 3 Ом. Визначити фазні і лінійні струми і напруги в таких режимах:
в симетричному трифазному;
2) при обриві однієї фази;
3) при обриві лінійного проводу.
Побудувати для всіх режимів векторні діаграми струмів і напруг.
Розрахунок.
1) Симетричний режим (див. рис.).
Визначаємо комплексні вирази для фазних опорів і напруг:
Zф:= 4 + 3·j
Знаходимо комплексні вирази для фазних струмів:
Знаходимо комплексні вирази для лінійних струмів:
IA:= Iab – Ica IA = 75.663 – 9.116 j
IB:= Ibc – Iab IB = –29.937 + 70.084 j
IC:= Ica – Ibc IC = –45.726 – 60.958 j
Векторна діаграма напруг і струмів має вид:
2) Обрив однієї фази (див. рис.).
При обриві фази навантаження bc струм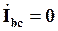 
. Струми 
і 
залишаються без змін, тому колишнє значення має і струм 
. Струми 
і 
змінюються: 
.
Векторна діаграма струмів матиме вид:
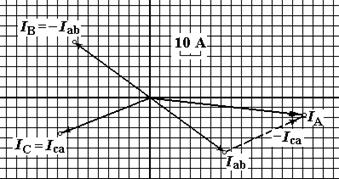
3) Обрив лінійного проводу (див. рис.).
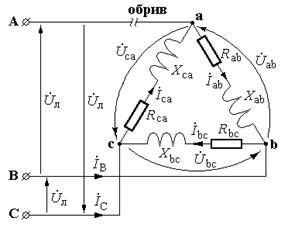При обриві лінійного проводу А–а опори у вітках са і ab виявляються з’єднані послідовно. Отже, на кожний з цих опорів припадає половина лінійної напруги UBC, оскільки опори у вітках са і ab однакові (Zф). Визначаємо комплексні вирази для лінійних напруг, що прикладені до опорів віток у випадку обриву лінійного проводу:
Приймаємо 
, тоді: за другим законом Кірхгова для контура abc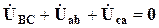 
,
звідки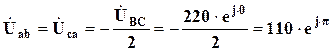 
.
Знаходимо комплексні вирази для фазних струмів:
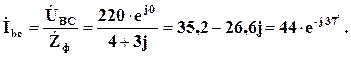
Знаходимо комплексні вирази для лінійних струмів:
Векторні діаграми напруг і струмів матимуть вид:
Приклад 2. До трифазної лінії з лінійною напругою U л = 380 В підключене несиметричне навантаження, з’єднане за схемою «зірка» з нейтральним проводом. Активні і реактивні опори фаз навантаження R а = 10 Ом, Х а = 0; R b= 3 Ом, Х b= 4 Ом; R с = 9Ом, Х с = –12 Ом.
Опір нейтрального проводу нехтовно малий. Визначити фазні і лінійні струми і напруги в таких режимах:
1) трифазному;
2) при обриві лінійного проводу;
3) при короткому замиканні фази навантаження і обриві лінійного проводу.
Побудувати для всіх режимів векторні діаграми струмів і напруг.
Розрахунок.
1) Несиметричний трифазний режим (див. рис.).
Визначаємо комплексні зображення фазних напруг:
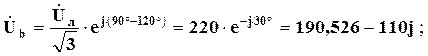
Знаходимо зображення фазних струмів:
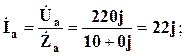
Вираховуємо зображення струму в нульовому проводі:
Знаходимо зображення лінійних напруг:
Векторна діаграма струмів і напруг матиме вигляд:
2) Обрив лінійного проводу (див. рис.).
При обриві лінійного проводу А–а струм І А у фазі А відсутній, тобто струм І а = 0; струми І b і І c мають такі ж напрямки, як і у трифазному режимі.
Струм у нульовому проводі:
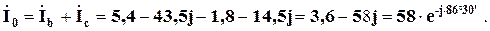
Фазна напруга U a відсутня (U a = 0); напруги U b і U c направлені як і трифазному режимі.
Знаходимо лінійні напруги на навантаженнях при обриві лінійного проводу А–а:
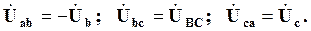
Векторна діаграма струмів і напруг матиме вид:
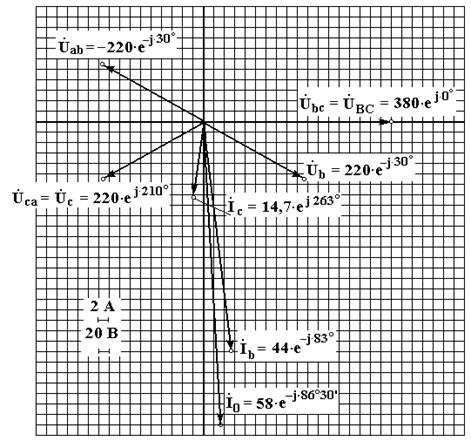
3) Коротке замикання фази навантаження і обрив нейтрального проводу (див. рис.).
Запишемо вирази для фазних напру мережі:
Знаходимо напругу U 0:
Визначаємо фазні напруги на навантаженнях при заданому режимі:
звідки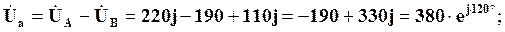 
звідки 
Знаходимо фазні струми:
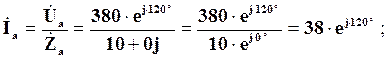
Векторна діаграма струмів і напруг:
Питання для самоперевірки до розділу «Електротехніка»
1. Які проблеми вивчає електротехніка?
2. Дайте визначення поняттям: електрична схема, вузол, вітка, контур, струм, напруга, ЕРС, потужність.
3. Які елементи включає зовнішнє коло джерела?
4. Які узгодження приймаються щодо додатних напрямків струму та напруги?
5. Що називають активним опором?
6. Що називають лінійним опором? ВАХ лінійного і нелінійного опорів.
7. Які кола називають лінійними і нелінійними?
8. Яка різниця між простими і складними електричними колами?
9. Сформулюйте основні закони електротехніки.
10. Що розуміють під балансом потужностей у колі?
11. Напруга на клемах джерела.
12. Ідеальні і реальні джерела напруги і струму, їх вольт-амперні характеристики.
13. Режими роботи кола постійного струму.
14. Особливості послідовного з’єднання споживачів.
15. Особливості паралельного з’єднання споживачів.
16. Для чого використовується послідовне, паралельне та змішане з’єднання гальванічних елементів?
17. Еквівалентні перетворення в електричних колах.
18. Які задачі вирішуються в розрахунках електричних кіл?
19. Принципи розрахунку простих електричних кіл.
20. Сформулюйте закони Кірхгофа.
21. В чому полягає безпосереднє використання законів Кірхгофа в розрахунку складних електричних кіл?
22. Суть методу контурних струмів.
23. Суть методу вузлових напруг.
24. Що називають активним двополюсником?
25. Сутність методу еквівалентного генератора.
26. Основні принципи методу накладень (суперпозиції).
27. Сутність графоаналітичного методу розрахунку нелінійних кіл з послідовним, паралельним і змішаним з’єднанням нелінійних елементів.
28. Які ЕРС, напруги і струми називають змінними?
29. Які нові елементи проявляють свої властивості в колах змінного струму?
30. Основні параметри синусоїдального змінного струму, напруги, ЕРС.
31. Що визначають поняття початкова фаза і зсув фаз?
32. Що розуміють під діючим значенням?
33. Яку величину напруги показує вольтметр, включений у звичайну розетку вашої квартири?
34. Як визначається потужність р на змінному струмі?
35. Способи зображення синусоїдальних змінних величин: аналітичний; графічний; через вектори, що обертаються; через комплексні числа.
36. Що називають топографічною діаграмою?
37. Як проявляє себе активний опір на синусоїдальному змінному струмі? Як змінюється миттєве значення потужності на активному опорі?
38. Що називають індуктивністю і в чому її прояв? Як індуктивність змінює фазу струму відносно синусоїдальної напруги?
39. Як змінюється миттєве значення потужності на індуктивності? Що означає від’ємне значення потужності?
40. Що характеризує ємність? Як ємність змінює фазу струму відносно синусоїдальної напруги?
41. Що називають реактивним опором?
42. Як залежать реактивні опори індуктивності і ємності від частоти?
43. Розкажіть про співвідношення напруги і струму в ланцюзі з послідовно з’єднаними активним опором, індуктивністю і ємністю. Дайте визначення поняттю «повний опір кола».
44. Поясніть поняття повна, активна і реактивна провідності.
45. Поясніть побудова векторних діаграм для послідовного з’єднання активного опору, індуктивності і ємності.
46. Поясніть побудова векторних діаграм для паралельного з’єднання активного опору, індуктивності і ємності.
47. Обґрунтуйте еквівалентну заміну послідовного з’єднання паралельним. Проілюструйте доцільність такої заміни для кола із змішаним з’єднанням елементів r, L, C.
48. Поясніть сутність символічного методу розрахунку кіл синусоїдального змінного струму. Чи можна використовувати цей метод для кіл, в яких діють струми і напруги довільної форми?
49. Запишіть вирази для зображень напруги і струму для найпростіших кіл: із активним опором; із індуктивністю; із ємністю.
50. Поясніть поняття активна, реактивна і повна потужності. Які вирази їх визначають?
51. Поясніть поняття «трикутник напруг, опорів, потужностей». Поясніть, чому індуктивному і ємнісному опорам приписуються різні знаки.
52. Як визначається коефіцієнт потужності? Поясніть його значення.
53. Поясніть роботу фазоперетворювача.
54. Поясніть сутність коливального процесу в електричному колі.
55. Які елементи складають коливальний контур? Поясніть поняття «частота власних коливань коливального контуру».
56. Яке явище називається резонансом напруг? Складіть умова резонансу напруг і поясніть зміною яких параметрів можна досягти режим резонансу.
57. Чи може у колі, що включає послідовно з’єднані елементи L і C, утворюватись напруга більша за напругу живлення? Якщо так, то за яких умов?
58. За допомогою яких приладів і за якими ознаками можна судити про настання резонансу напруг? Накресліть частотні характеристики послідовного коливального контуру і поясніть їх форму.
59. Поясніть поняття «добротність» коливальної системи.
60. Які прояви резонансу струмів мають місце?
61. Що називають багатофазними системами змінного струму?
62. Поясніть, які переваги має трифазна система.
63. Як утворюється трифазна система ЕРС в генераторі?
64. Що може означати в електротехніці термін «фаза»?
65. Поясніть сутність термінів «лінійний провід», «нульовий або нейтральний провід», «нульова точка генератора» та «нульова точка навантаження».
66. Як називають і маркують проводи, що відходять від трифазного генератора? Які напруги і струми існують в трифазній мережі?
67. Що означає «фазна напруга» та «лінійна напруга»?
68. Що означає «фазний струм» та «лінійний струм»?
69. Які існують залежності між діючими лінійними і фазними напругами і струмами трифазної чотирипровідної мережі?
70. Як визначається струм в нульовому проводі?
71. У яких випадках доцільно використовувати трифазне коло з нейтральним проводом і без нього? Чому в нейтральний провід не включають запобіжники, роз'єднувачі?
72. Які існують залежності між діючими лінійними і фазними напругами і струмами трифазної трипровідної мережі?
73. Який режим роботи трифазного кола називають симетричним? Яку роль відіграє нейтральний провід у трифазних колах?
74. Як вимірюється потужність в трифазній чьотирьох і трипровідній мережі?
75. Поясніть поняття «зміщення нейтралі».
76. Що означає «схема з’єднання обмоток генератора трикутником»? Чи виникає при цьому струм в контурі генератора?
77. Які існують залежності між лінійними і фазними струмами і напругами трифазної системи при з’єднанні споживачів трикутником?
78. Під дією якої напруги знаходяться споживачі при їх з’єднанні «трикутником»?
79. Як зміняться струми і потужність трифазного кола, якщо включені за схемою «зірка» однакові опори, перемкнути на схему «трикутник»?
80. Які співвідношення між фазними і лінійними струмами споживачів, з’єднаних трикутником у випадках: а) обриву однієї з фаз; б) обриву лінійного проводу?
81. Що означає «захисне заземлення»? Які вимоги накладаються до захисного заземлення?
82. Чим відрізняється «заземлення» від «занулення»?
