Особливості розрахунку кіл змінного струму

Змінними називаються ЕРС, напруги і струми, які змінюються в часі.

В сучасному електроустаткуванні найбільше застосування отримали змінні струми, величина (і напрямок) яких періодично змінюються за синусоїдальним законом – синусоїдальні струми.

Значення змінних величин (ЕРС, напруг, струмів, потужностей) в будь-який момент часу називаються миттєвими і позначаються буквами е, u, i, p.

Для синусоїдальних струмів миттєве значення визначається виразом i = I _m sin (w t + y), де I _m – найбільше миттєве значення періодично змінюваних величин, яке називається амплітудним значенням. Аналогічно визначаються синусоїдальні напруги u = U _m sin (w t + y) та ЕРС e = E _m sin (w t + y).

Аргумент синусу − кут (w t + y) називається фазою.

Час Т, за який струм (напруга, ЕРС) здійснює повний цикл своїх змін називають періодом змінного струму (напруги, ЕРС), а число періодів за секунду – його циклічною частотоюf = 1/ T. Одиниця частоти – Гц. Частота дорівнює 1 Гц, якщо повний цикл зміни струму здійснюється за 1 секунду.

Синусоїдальний характер змінного струму зумовлений характером змінної ЕРС, що утворюється в статорі генератора. Ротор обертається з кутовою швидкістю w = a / t. Якщо покласти a = 2p (повний оберт), а це буде за час t = Т, за який струм, як зазначалось, здійснить повний цикл своїх змін,то w = 2p / Т = 2p f. Ця величина (w) називається круговою частотою.

Від спостерігача залежить з якого моменту почати спостереження за зміною струму. Тому у виразі i= I _m sin (w t + y) присутня величина y, що називається початковою фазою, і яка визначає відставання моменту початку спостереження від початку поточного періоду[8]. Якщо y = 0, то i = I _m sinw t.

 

 

Між двома синусоїдальними величинами, що мають різні початкові фази, наприклад, y _u і y _i , існує зсув фазj = y _u – y _i. (див. рисунок) Ця величина більш цікава, оскільки при дослідженні двох синусоїдальних величин завжди початкову фазу однієї можна взяти нульовою, тоді початкова фаза іншої становитиме j і вже не залежатиме від суб’єктивного вибору початку спостереження.

Діюче значення змінного струму дорівнює значенню еквівалентного постійного струму, який утворює на незмінному опорі стільки ж теплоти, як і змінний струм.

Діюче значення змінного синусоїдального струму менше його амплітудного значення в раз. Таке ж співвідношення між діючими і амплітудними значеннями для напруг і ЕРС. Діючі значення позначаються I, U, E.

Отже для аналізу синусоїдального струму необхідно знати: амплітудне (І _m, U _m, E _m) або діюче (І, U, E) значення; частоту коливань (w, f або Т: w = 2p f, f = 1/ T) і початкову фазу y.

Для розрахунків кіл змінного струму використовується зображення синусоїдальних величин за допомогою векторів, що обертаються.

Нехай маємо струм i = I _m sin(w t + y).

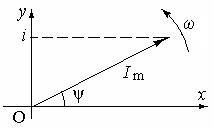Для того, щоб зобразити його вектором, що обертається візьмемо прямокутну систему координат хОу. Із початку координат О під кутом y проведемо вектор 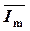, довжина якого в масштабі відповідає I _m. Якщо вектор 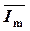обертати проти годинникової стрілки з кутовою швидкістю w = 2p f, то його проекція на вісь ординат Оу буде змінюватись за синусоїдальним законом, тобто відображатиме миттєве значення струму і.

Сукупність векторів, що зображують на одному кресленні кілька синусоїдальних величин однієї частоти має назву векторна діаграма.

Вектори, що зображені на такій діаграмі мають однакову кутову частоту w. Тому при обертанні, їх взаємне розміщення не змінюється. Отже при побудові векторних діаграм один вектор завжди можна направити довільно (наприклад, вздовж Ох), а інші розташовувати по відношенню до першого під різними кутами, що дорівнюють відповідним кутам зсуву фаз, і осі координат не креслити.

В більшості випадків векторні діаграми кіл змінного струму призначені для визначення співвідношень між діючими значеннями напруг і струмів. Тому діаграми звичайно будують не для амплітудних значень, а для діючих, що зумовлює лише зменшення довжини векторів в разів.

Якщо векторну діаграму будують в тій же послідовності, в якій обходять електричне коло, вона називається топографічною. Топографічна діаграма дозволяє визначити напругу між будь-якими точками кола, оскільки кожна точка діаграми відповідає певній точці кола. Для визначення треба з’єднати дві точки діаграми відрізком і надати йому відповідний напрямок.

При побудові топографічної діаграми один з векторів приймають за вихідний і розташовують вздовж горизонтальної осі в додатному напрямку, вважаючи, що початкова фаза відповідної йому величині дорівнює нулю. Інші вектори будують відносно цього вектора з урахуванням фазового зсуву послідовно один за одним, беручи за початок координат кінець попереднього вектора. Зручно для послідовного кола за вихідний приймати вектор струму, а для паралельного – напруги, тобто вектори величин, однакових для всіх елементів.Таким чином вже можна передбачити, що при розрахунках кіл змінного струму треба буде використовувати складні перетворення з величинами, до яких входять тригонометричні функції, або виконувати графічні дії над векторами.

Ефективним методом розрахунку кіл змінного струму є символічний метод, оснований на зображенні електричних величин (струм, напруга, ЕРС, опори, провідності, потужності) комплексними числами. В цьому випадку для розрахунку кіл змінного струму можна використовувати закони Кірхгофа і всі методи розрахунку складних кіл постійного струму.

Форми запису комплексних чисел[9]:

q В алгебраїчній формі комплексне число Z є сума дійсного числа a і уявного числа jb, тобто Z = a + jb. Уявне число jb є добуток уявної одиниці і коефіцієнта при ній b.

q Для зображення комплексного числа в графічній формі в прямокутній системі координат по горизонтальній осі відкладаються дійсні частини комплексного числа а, а по вертикальній осі – уявні частини jb. Комплексне число на такій комплексній площині зображується:

¨ точкою з координатами А (a; jb);

¨ вектором ОА, що починається в початку координат О, а закінчується в точці А з координатами (a; jb).

q Щоб записати комплексне число в показовій формі треба знати його модуль і аргумент. Модуль є довжина вектора ОА на комплексній площині: . Аргумент – це кут a між додатним напрямком дійсної осі і вектором ОА. Ясно, що b/a = tg a, звідки a = arctg b/a.

При визначенні a треба мати на увазі, що обчислювальні засоби дають значення arctg b/a в межах 0°£ a£ 90°. Тому отримане значення слід відкоригувати згідно таблиці:

 

а	b	чверть	a =
+	+	І	arctg b/a
–	+	ІІ	180° – arctg b/a
–	–	ІІІ	180° + arctg b/a
+	–	IV	– arctg b/a

 

Комплексне число в показовій формі є добуток модуля і множника е ^ja, тобто Z = |Z|× е ^ja.

q Тригонометрична форма. При розрахунках із використанням комплексних чисел виникає потреба перейти від показової форми до алгебраїчної. Вихідними є модуль і аргумент. Необхідно визначити дійсну та уявну частини і представити число в алгебраїчній формі.

З трикутника a = |Z|× cos a, b =|Z|× sin a.

В комплексній формі Z = a + jb = |Z|× cos a + j|Z|× sin a

Отриманий запис є тригонометричною формою комплексного числа.

Для додавання або віднімання двох комплексних величин зручніше використовувати алгебраїчну форму:

Z ₁ ± Z ₂ = a ₁ + jb ₁ ± a ₂ + jb ₂ = (a ₁± a ₂) + j (b ₁ ± b ₂).

Для множення і ділення – зручніше використовувати показову форму:

Z ₁ ´ Z ₂ = | Z ₁ | e ^ja ´ | Z ₂| e ^jb = | Z ₁ | ´| Z ₂| e ^{j(a + b)};

Z ₁ / Z ₂ = | Z ₁ | e ^ja / | Z ₂| e ^jb = | Z ₁ | / | Z ₂| e ^{j(a – b)},

але можна і алгебраїчну:

Z ₁ ´ Z ₂ = (a ₁ a ₂ – b ₁ b ₂) + j (a ₁ b ₂ + b ₁ a ₂); .

Два комплексних числа називаються спряженими, якщо відрізняються тільки знаками уявної частини (в алгебраїчній формі), або знаками аргументів (в показовій формі), наприклад:

a + jb та a – jb;

| Z| e ^ja та | Z| e ^–ja .

Повертаючись до електричних величин можна провести аналогію між векторами, що обертаються, і векторами, що зображують комплексні числа, якщо перші будувати на комплексній площині. Ця аналогія дозволяє синусоїдальні величини зображувати комплексними числами, а для арифметичних операцій над синусоїдальними величинами використовувати вже відомий математичний апарат. Зображення струмів, напруг і ЕРС у вигляді комплексних чисел прийнято позначати .

Побудуємо для кіл з активним опором, індуктивністю і ємкістю векторні діаграми, але вже на комплексній площині, вважаючи, що розташування вектора величини з нульовою початковою фазою співпадає з дійсною додатною піввіссю.

В усіх випадках вектор напруги направлений по осі дійсних чисел, оскільки будемо вважати його початкову фазу рівною 0°. Тому комплекс напруги , де U – модуль комплексу напруги, а 0° – його початкова фаза. Комплекс струму:

у першому випадку –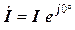

у другому випадку –

у третьому випадку –

Отже комплексне зображення синусоїдальних величин визначає її діюче (або амплітудне) значення і зсув фаз відносно вихідної величини, початкова фаза якої вважається рівною нулю.

При розрахунку кіл синусоїдального змінного струму використовуються закони Кірхгофа, що справедливі для миттєвих, амплітудних та діючих значень:

для миттєвих значень – суми алгебраїчні.

Ці рівняння справедливі у векторній формі, тобто суми не алгебраїчні, а геометричні.

Суми алгебраїчні завдяки зображенню електричних величин комплексними числами.

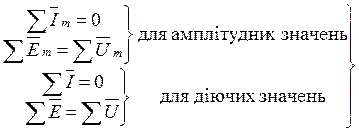
Розглянемо кола «а» і «б»:

В обох випадках вектор струму направлений по осі дійсних чисел[10], оскільки будемо вважати його початкову фазу рівною 0°. Комплекс напруги на клемах кола:

для випадку а) ,

де U _a і jU _L – дійсна і уявна частини; U і j — модуль і початкова фаза комплексу напруги.

для випадку б) .

В загальному виразі комплексу напруги «+» перед уявною частиною свідчить, що в навантаженні переважає опір індуктивності − навантаження має індуктивний характер, або активно-індуктивний; «–» − в навантаженні переважає опір ємності − характер навантаження ємнісний, або активно-ємнісний.

Розглянемо електричне коло, що складається з трьох елементів:

, де

, а аргумент .

j > 0, якщо U _L > U _C, як у випадку «а»;

j < 0, якщо U _L < U _C, як у випадку «б»[11].

Розрізняють повний опір Z, реактивний опір X і активний опір R, а також відповідні їм провідності: повна провідність – y = 1 / Z, реактивна провідність – b = X / Z ² і активна провідність – g = R / Z ².

З розглянутих трикутників напруг (наприклад, «а» і «б») = .

Це відношення є законом Ома. – повний опір кола і позначається Z. . Тобто I = U / Z.

Якщо сторони трикутників напруг «а» і «б» поділити на струм І, то отримаємо трикутник опорів, тобто активний, реактивний[12] і повний опори пов’язані між собою як сторони трикутника.

Ці трикутники також можна побудувати на комплексній площині і тоді опори виражатимуться комплексними числами:

= R + jX = R + j (X _L – X _C),

де .

Отже зображення опорів мають вид:

Аналогічно визначаються провідності: .

При записі повної провідності в показовій формі:

модуль комплексу опору – ; аргумент – .

Якщо сторони трикутника напруг помножити на струм І, то отримаємо трикутник потужностей:

Активна потужність – P = U _a ×I = UI × cos j [вт];

Реактивна потужність – Q = U _Х ×I = UI× sіn j [вар];

Повна потужність – S = U×I [в × а].

Формули законів Ома і Кірхгофа для кіл змінного струму в комплексній формі мають таку ж структуру, як і для кіл постійного струму. Тому методи розрахунку лінійних кіл постійного струму, що були вже розглянуті (метод безпосереднього використання законів Кірхгофа, метод суперпозиції, метод контурних струмів, метод вузлових потенціалів, метод еквівалентного генератора), можна застосовувати для розрахунку складних лінійних кіл синусоїдального змінного струму. В цьому випадку всі ЕРС, напруги, струми, опори і провідності ділянок кола визначаються так же, як і в колах постійного струму, але в комплексній формі.

Порядок розрахунку електричних кіл змінного синусоїдального струму такий:

1. Всі задані вихідні дані, включаючи напруги і струми джерел, активні і реактивні опори електричного кола представляються комплексними числами, тобто на першому етапі здійснюється перехід від оригіналів вихідних даних до їх зображень.

2. Для отриманих зображень вихідних даних здійснюється розрахунок електричного кола одним з методів, розглянутому в теорії кіл постійного струму, і отримують зображення результатів розрахунків.

3. Здійснюється перехід від зображень результатів розрахунку до їх оригіналів.

Приклад 1. Використовуючи метод контурних струмів визначити розподіл струмів у вітках наведеної схеми:

Вихідні дані:

R₁ = 1 кОм, R₂ = 1 кОм, R₃ = 2 кОм, R₄ = 0,8 кОм, R₅ = 4 кОм, C₁ = 1 нФ, C₂ = 2 нФ, C₃ = 0,5 нФ, C₄ = 0,4 нФ, L = 4 мГн, Е₁ = 80∙sin(ω t) В, Е₂ = 120∙sin(ω t + 45°) В, ω:= 5·10⁶.

Розрахунок проводиться в середовищі MathCAD:

ORIGIN:= 1

Вихідні дані:

R₁:= 1000 R₂:= 1000 R₃:= 2000 R₄:= 800 R₅:= 4000

С₁:= 1·10^–9 С₂:= 2·10^–9 С₃:= 0.5·10^–9 С₄:= 0.4·10^–9 L:= 4·10^–3

Е₁:= 80·е ^j·0 Е₂:= 120·е ^{j·π / 4} ω:= 5·10⁶

Схема включає три контури: acdba, cefdc, eghfe.

Матриця зображень коефіцієнтів розрахункової системи рівнянь:

Вектор правих частин розрахункової системи рівнянь:

Розв’язання системи рівнянь відносно зображень контурних струмів:

Комплексні зображення струмів у вітках[13]:

І₁:= І ₁ І₂:= І ₁ – І ₂ І₃:= І ₂ І₄:= І ₃ – І ₂ І₅:= І ₃

І₁ = 0.017 + 7.561j ´ 10^–4 I₂ = 0.016 + 2.636j ´ 10^–4

І₃ = 5.757 ´ 10^–4 + 4.925j ´ 10^–4 І₄ = 0.016 + 0.025j І₅ = 0.016 + 0.025j

Перехід від зображень до оригіналів струмів:

Аналітичні вирази для струмів у вітках[14] (i = І_m·sin(ωt + ψ):

| I₁ | = 0.017 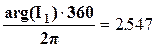і ₁ = 0.017·sin(5·10⁶· t + 2,547°)

| I₂ | = 0.016 і ₂ = 0.016·sin(5·10⁶· t + 0,944°)

| I₃ | = 7.576E–4 і ₃ = 7.576E –4 ·sin(5·10⁶· t + 40,546°)

| I₄ | = 0.03 і ₄ = 0.03·sin(5·10⁶· t + 57,381°)

| I₅ | = 0.03 і ₅ = 0.03·sin(5·10⁶· t + 57,381°)

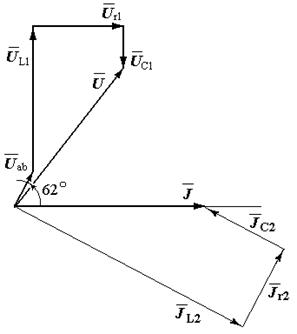
Приклад 2. Визначити розподіл струмів і напруг в простому колі змінного струму. Побудувати векторну діаграму.

Вихідні дані:

r ₁ = 6 Ом; L ₁= 25,5 мГ; С ₁= 1590 мкф; r ₂= 5 Ом; L ₂ = 5 мГ; С ₂ = 1000 мкф; U = 127 В; f = 50 Гц.

Розрахунок:

1. Визначаємо Z ₁– повний опір з’єднаних послідовно елементів r ₁, L ₁, С ₁:

X _L1 = 2 π f · L ₁= 2·3,14·50·25,5·10^–3 = 8 Ом;

Х _C1 = 1/(2 π f · С ₁) = 1/(2·3,14·50·1590·10^–6) = 2 Ом;

2. Визначаємо y ₂ – повну провідність[15] паралельної частини схеми:

X _L2 = 2 π f · L ₂ = 2·3,14·50·5·10^–3 = 1,57 Ом;

Х _С2 = 1/(2 π f · С ₂) = 1/(2·3,14·50·1000·10^–6) = 3,18 Ом;

3. Знаходимо повний опір схеми (Z), струм (J)і напруги (U _r1, U _L1, U _C1, U _аb):

Z = Z _l + Z ₂ = Z _l + l / y ₂ = 8,5 + 2,63 = 11,13 Ом;

J = U / Z = 127 / 11,13 = 11,4 А;

U _r1 = J · r ₁ = 11,4·6 = 67,3 В;

U _L1 = J · X _L1 = 11,4·8 = 91 B;

U _C1 = J · X _C1 = 11,4·2 = 22,8 В;

U _ab = J · Z ₂ = 11,4·2,63 = 30 В;

4. Визначаємо струми у вітках розгалуженої частини схеми:

J _r2 = U _ab / r ₂ = 30 / 5 = 6 А;

J _L2 = U _ab/ X _L2= 30 /1,57 = 19,1 А;

J _C2 = U _ab/ X _C2= 30 / 3,18 = 9,4 А;

5. Визначаємо зсув фаз між напругою U _ab і струмом J:

b _L2=1/ Х _L2 =1 /1,57 = 0,64; b _С2= 1 / Х _С2 = 1 /3,18 = 0,315;

φ = arcsin(b / y)=arcsin ((b _L2 – b _C2) / y ₂) = arcsin(0,335 / 0,38) = arcsin0,885 Þ φ = 62°.

6. Будуємо векторну діаграму струмів і напруг схеми, для чого обираємо масштаби струмів і напруг: т _j = 0,4:1 А/мм; т _U = 4:1 В/мм.

За базовий обираємо вектор струму J, оскільки він є спільним для послідовної і паралельної частин схеми, і відкладаємо його у відповідному масштабі по горизонталі[16].

Враховуючи індуктивний характер розгалуженої частини кола (b _L2 > b _C2),відкладаємо під кутом φ = 62° вектор напруги .

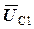У відповідності з рівнянням будується векторна діаграма напруг з урахуванням кутів зсуву фаз між струмом i напругами на елементах. Вектор напруги випереджає вектор струму на 90°, вектор напруги співпадає за напрямком з вектором струму ,а вектор напруги відстає від вектора струму на 90°:

Потім будується векторна діаграма струмів. Для цього за базисний приймається вектор ,спільний для паралельної частини схеми, і відносно нього будуємо діаграми струмів, використовуючи формулу 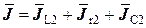i фазові співвідношення між відповідними величинами: