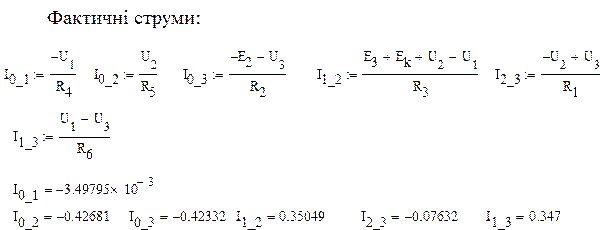Універсальним методом розрахунку складних кіл є метод безпосереднього використання першого закону Кірхгофа для вузлових точок і другого закону Кірхгофа для замкнутих контурів схеми.
Якщо відомими є величини ЕРС і їх напрямки, а також опори складного кола, то застосовуючи закони Кірхгофа можна скласти стільки незалежних рівнянь, скільки невідомих струмів в цьому колі. Ці рівняння утворюють систему лінійних алгебраїчних рівнянь, розв’язавши яку можна отримати значення невідомих струмів.
Для складання рівнянь необхідно попередньо позначити на схемі довільно обрані додатні напрямки невідомих струмів. Якщо в результаті розв’язання складеної системи рівнянь знайдена величина струму має знак «+», то його фактичний напрямок співпадає з довільно обраним, В протилежному випадку фактичний напрямок струму протилежний обраному напрямку.
Розрахунок складного кола через рівняння Кірхгофа виконується в такій послідовності:
1. При можливості спрощують розрахункову схему (наприклад, можна замінити кілька паралельно або послідовно з’єднаних опорів одним еквівалентним опором).
2. Позначають на схемі відомі напрямки ЕРС.
3. Позначаються довільно обрані напрямки струмів.
4. Складають рівняння за першим законом Кірхгофа для всіх вузлових точок, крім однієї. Якщо схема містить п вузлів, то незалежних рівнянь можна скласти тільки для (п – 1) вузлів.
5. Складають рівняння, за кількістю яких бракує, за другим законом Кірхгофа (відомо, що для розв’язання системи необхідно, щоб кількість незалежних рівнянь дорівнювало кількості невідомих, в даному випадку струмів).
6. Розв’язують складену систему рівнянь і визначають невідомі струми.
Метод контурних струмів.
При розрахунку складних кіл, що складаються з невеликої кількості контурів, переважним є метод контурних струмів, який дозволяє скоротити загальну кількість рівнянь в системі.
 Сутність методу розглянемо на схемі кола з вузлами А, В, С, D.
Сутність методу розглянемо на схемі кола з вузлами А, В, С, D.
Ця схема включає три контури АВСА(І), ADBA(ІІ), CBDC(ІІІ). Кожному контуру умовно приписують довільно направлений контурний струм, однаковий для всіх ділянок цього контуру І І, І ІІ, І ІІІ. У вітках, які є спільними для двох суміжних контурів, фактичний струм дорівнює алгебраїчній сумі двох контурних струмів.
Тут:
- у вітці АС протікає струм І 1 = І І;
- у вітці АВ протікає струм І 2 = І ІІ – І І, оскільки контурний струм І ІІ співпадає за напрямом із шуканим струмом І 2, а контурний струм І І − протилежний напряму струму І 2;
- у вітці АD протікає струм І 3 = І ІI;
- у вітці DB – І 4 = І ІІ – І ІІІ
- у вітці ВС – струм І 5 = І І – І ІІІ;
- у вітці C D – І 6 = І ІІІ,
тобто всі шість шуканих струмів виражені через три контурних струми І І, І ІІ, І ІІІ.
Застосовуючи до кожного з контурів другий закон Кірхгофа, отримаємо систему з кількістю рівнянь, рівною кількості невідомих контурних струмів:
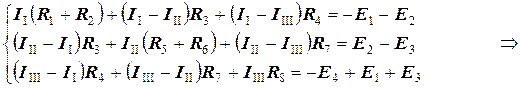
Отриману систему рівнянь доцільно переписати так, щоб шукані струми розташувались у відповідних стовпчиках, тобто привести систему до канонічної форми:

Розв’язавши систему і визначивши контурні струми І І, І ІІ, І ІІІ, неважко знайти струми у вітках схеми: I 1 = I I, I 2 = I II – I I, I 3 = I II, I 4 = I II – I III, I 5 = I I – I III, I 6 = I III.
Зауважимо, що при безпосередньому використанні законів Кірхгофа для розрахунку цієї схеми необхідно було б розв’язати систему з шести рівнянь.
Приклад. Робочий листок MathCAD визначення струмів при конкретних значеннях вихідних даних для наведеної схеми має вид:
ORIGIN:= 1
Вихідні дані:
R 1 := 10 R 2 := 20 R 3 := 50 R 4 := 8 R 5 := 40 R 6 := 25 R 7 := 35 R 8 := 40
E 1 := 12 E 2 = 24 E 3 = 12 E 4 = 15
Матриця коефіцієнтів розрахункової системи рівнянь:

Матриця правих частин:
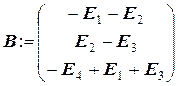
Розв’язання системи рівнянь АІ=В:

Фактичні струми [6]:
I 1:= I 1 I 2:= I 2 – I I I 3:= I 2 I 4:= I 2 – I 3 I 5:= I 1 – I 3 I 6:= I 3
I 1 = –0.437 I 2 = 0.381 I 3 = –0.056 I 4 = –0.098 I 5 = –0.48 I 6 = 0.043
При складанні балансу потужностей якщо дійсний напрямок ЕРС і струму у вітці співпадають, то джерело ЕРС працює в режимі генератора і віддає потужність у коло. Якщо напрямки ЕРС і струму протилежні, то джерело ЕРС працює в режимі приймача електроенергії і споживає потужність.
Перевірка:
Потужність, що постачається в коло:
|E 1· I 5| + |E 2 · I 2| + |E 3 · I 4| = 16.086
Потужність, що споживається в колі:
I 1 2·(R 1 + R 2) + I 2 2· R 3 + I 3 2·(R 5 + R 6) + I 4 2· R 7 + I 5 2· R 4 + I 6 2· R 8 + E 4· I 6 = 16.086
Як видно, потужність, що віддається в коло джерелами, збігається з потужністю, що споживається елементами кола.
Метод вузлових напруг.
Коли електричне коло складається з великої кількості контурів при невеликій кількості вузлів, його аналіз доцільно здійснювати методом вузлових напруг (інша назва – метод вузлових потенціалів).
Якщо кількість вузлів в схемі n, то кількість рівнянь, необхідних для розрахунку такого кола дорівнює (п – 1). Невідомими величинами в цих рівняннях є так звані вузлові напруги. У відповідності з цим методом потенціал в одному з вузлів схеми приймають рівним нулю. В інших вузлах схеми встановлюються потенціали, які відносно вузла з нульовим потенціалом будуть утворювати відповідно вузлові напруги U 1, U 2,..., U n–1.
Струм в кожній вітці схеми визначається напругами, прикладеними до вузлів вітки (вузловими напругами), ЕРС, якщо вітка їх містить і опором вітки.
Сутність методу полягає у наступному. Використовуючи вирази для струмів через вузлові напруги, ЕРС та опри, складають рівняння за першим законом Кірхгофа для кожного вузла схеми за виключенням вузла з нульовою напругою. Сукупність таких рівнянь утворює систему рівнянь відносно невідомих вузлових напруг.
При складанні рівняння для будь-якого і -го вузла можна скористатись вже готовою універсальною формулою:

за якою:
добуток вузлової напруги в і –тому вузлі на суму провідностей віток між і –тим і кожним з сусідніх з і –тим вузлами,
мінус сума добутків вузлових напруг в кожному сусідньому з і –тим вузлі на провідність вітки між цим вузлом і і –тим,
дорівнює сумі добутків ЕРС у вітці між і– тим і кожним сусіднім з і –тим вузлі (якщо вона є у цій вітці) на провідність цієї вітки.
Складові Е ij беруться із знаком “+”, якщо ЕРС направлена до і –го вузла і із знаком “–”, якщо вона направлена від і –го вузла.
Розв’язавши систему відносно U і, можна визначити струми у вітках.
Приклад. Розглянемо розрахунок електричного кола за цим методом на прикладі схеми, наведеній на рисунку.

а) б)
Значення параметрів:
Вихідні дані: E 2 = 20 В; E 3 = 7,6 В; Е К = 4,4 В; R 1 = 12 Ом; R 2 = 35 Ом; R 3 = 22 Ом; R 4 = 6 Ом; R 5 = 10 Ом; R 6 = 15 Ом.
1. Довільно пронумеруємо вузли схеми, починаючи з нуля. Потенціал у нульовому вузлі покладаємо рівним нулю і проставляємо позитивні напрямки вузлових напруг U I, U II, U III (див. рисунок «а»).
2. Для трьох вузлів, окрім нульового − (n −1), використовуючи наведену формулу, складаємо загальну систему рівнянь одразу в канонічній формі:
§ для вузла І: 
§ для вузла ІІ: 
§ для вузла ІІІ: 
Підставляючи числові значення опорів і ЕРС отримуємо закінчений вид системи лінійних алгебраїчних рівнянь:
 0,278788×U I – 0,04545×U ІІ – 0,06667×U ІІІ = 0,54545455
0,278788×U I – 0,04545×U ІІ – 0,06667×U ІІІ = 0,54545455
–0,04545×U I + 0,228788×U ІІ – 0,08333×U ІІІ = –0,54545455
–0,06667×U I – 0,08333×U ІІ + 0,178571×U ІІІ = –0,57142857
Відзначимо, що матриця коефіцієнтів отриманої системи, як і в попередньому випадку, симетрична.
Робочий листок MathCAD складання і розвʼязання системи рівнянь для зазначеної задачі має вид:



Розв’язання системи рівнянь AU = B
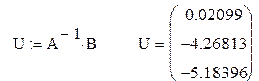
Розв’язуючи дану систему відносно U I, U II, U III, одержуємо:
U I = 0,020988 В; U II = –4,26813 В; U III = –5,18396 В.
3. Використовуючи другий закон Кірхгофа, визначаємо напругу на елементах схеми. Для цього на схемі крім позитивних напрямів вузлових напруг позначимо ще й напруги на всіх резисторах (див рисунок «б»). Тоді:
U III – U 1 – U IІ = 0 Þ U 1 = U IІІ – U II = –5,18396 В –(–4,26813 В) = –0,91583 В;
U III + U 2 + E 2 = 0 Þ U 2 = –U III – E 2 = –(–5,18396 В) – 20 В = –14,81604 В;
U I + U 3 – E к – E 3 – U II = 0 Þ U 3 = E к + E 3 + U II – U I = 12 В + (–4,26813 В) – 0,020988 В = 7,710879 В.
U 4 = –U I = –0,020988 В;
U 5 = U II = –4,26813 В;
U III + U 6 – U I = 0 Þ U 6 = U I – U III = 0,020988 В –(–5,18396 В) = 5,204948 В;
За законом Ома знаходимо струми у вітках:
I 1 = U 1/ R 1 = –0,91583/12 = –0,076319 A;
I 2 = U 2/ R 2 = –14,81604/35 = –0,42332 A;
I 3 = U 3/ R 3 = 7,710879/22 = 0,35049 A;
I 4 = U 4/ R 4 = –0,020988/6 = –0,0035 A;
I 5 = U 5/ R 5 = –4,26813/10 = –0,42681 A;
I 6 = U 6/ R 6 = 5,204948/15 = 0,346997 A.
4. Виконується перевірка балансом потужностей.
Робочий листок MathCAD[7] визначення струмів і перевірка балансу потужностей для зазначеної задачі має вид: