Черт. 10. К примеру расчета 10

1 — плоскость действия изгибающего момента; 2 — центр тяжести

сечения растянутой арматуры

 

По формуле (37) определим площадь сжатой зоны бетона А_b:

мм².

 

Площадь наиболее сжатого свеса полки и стати­ческие моменты этой площади относительно осей х и у соответственно равны:

 

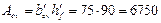мм²;

 

мм³;

 

мм³.

 

Так как А_b > А_ov, расчет продолжаем как для таврового сечения.

мм².

 

Составляющие изгибающего момента в плос­кости осей у и х соответственно равны (при ctg b = 4):

 

кН·м.

 

кН·м.

 

Определим по формуле (38) размер сжатой зо­ны бетона x ₁ по наиболее сжатой стороне сечения, принимая S_sy = 0:

 

 

Проверим условие (40):

 

 

Следовательно, расчет продолжаем по форму­лам косого изгиба.

 

Проверим условие (41) для наименее растяну­того стержня. Из черт. 10 имеем b _{0 i} = 30 мм, h _{0 i} = 400 – 30 = 370 мм:

 

 

 

(см. табл. 18).

Условие (41) не соблюдается. Расчет повторим, заменяя в формуле (37) значение R_s для наименее растянутого стержня напряжением s_s, определен­ным по формуле (42), корректируя значения h ₀и b ₀.

Из табл. 18 имеем w = 0,746 и y_c = 4,26.

 

 

Поскольку все стержни одинакового диаметра, новые значения А_b, b ₀ и h ₀ будут равны:

мм²;

 

мм;

 

мм.

Аналогично определим значения S_ov,y, S_ov,x и A_web:

 

 

 

Значение x ₁ определим по формуле (39):

 

 

 

Проверим прочность сечения из условия (35), принимая S_sx = 0:

 

 

т. е. прочность сечения обеспечена.

Пример 11. По данным примера 10 необходимо подобрать площадь растянутой арматуры при мо­менте в вертикальной плоскости М = 64 кН·м.

Расчет. Составляющие изгибающего момента в плоскости осей у и х равны:

 

 

 

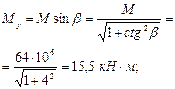
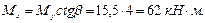
Определим необходимое количество арматуры согласно п. 3.25.

Принимая значения b ₀, h ₀, S _{0 v,x} , S _{0 v,y} , S_sy = = 0 из примера 10, находим значение a _mx и a _my:

 

 

 

Так как a _mx > 0, расчет продолжаем как для таврового сечения.

Поскольку точка с координатами a _mx = 0,227 и a _my = 0,114 на черт. 9 находится по правую сторону от кривой, отвечающей параметру и по левую сторону от кривой, отвечающей параметру арматура будет работать с полным расчетным сопротив­лением, т. е. условие (41) выполнено. Требуемую площадь растянутой арматуры определим по фор­муле (45).

По черт. 9 при a _mx = 0,227 и a _my = 0,114 нахо­дим a _s = 0,25. Тогда,принимая 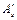= 0, имеем

 

мм².

 

Принимаем стержни 3 Æ 16 (A_s = 603 мм²) и располагаем их, как показано на черт. 10.

Пример 12. Дано: навесная стеновая панель общественного здания пролетом 5,8 м с попереч­ным сечением по черт. 11; бетон легкий класса В3,5, марки по средней плотности D1100; арма­тура класса А-III; нагрузки на панель в стадии эксплуатации: в плоскости панели — собственный вес и вес вышерасположенного остекления (вклю­чая простенки) высотой 3м 3,93 кН/м², из плоскости панели — ветровая нагрузка 0,912 кН/м²,

Требуется проверить прочность панели в стадии эксплуатации.