Основные законы и формулы
· Закон Кулона
 ,
,
где F – сила взаимодействия точечных зарядов q1 и q2;
r – расстояние между зарядами;
e – диэлектрическая проницаемость среды;
e0 – электрическая постоянная (e0=8,85×10-12 Ф/м).
· Напряженность  и потенциал j электрического поля:
и потенциал j электрического поля:
 ,
, 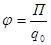
где F – cила, действующая на единичный точечный положительный заряд q 0, помещенный в данную точку поля;
Π – потенциальная энергия точечного положительного заряда q 0, находящегося в данной токе поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
· Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:
 ;
;  .
.
· Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции, или наложения, электрических полей):
 ,
, 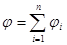 ,
,
где  ,
,  – напряженность и потенциал в данной точке поля, создаваемого i -ым зарядом.
– напряженность и потенциал в данной точке поля, создаваемого i -ым зарядом.
· Напряженность и потенциал поля, создаваемого:
1) точечным зарядом
 ,
,  ,
,
где r – расстояние от заряда q до точки, в которой определяются напряженность и потенциал;
2) проводящей заряженной сферой радиусом R на расстоянии r от центра сферы:
а) Е = 0;  (при r<R);
(при r<R);
б)  ;
;  (при r=R);
(при r=R);
в)  ;
;  (при r>R),
(при r>R),
где q – заряд сферы.
· Линейная плотность заряда
 ,
,
где l – длина заряженного тела.
· Поверхностная плотность заряда
 .
.
· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной линией или бесконечно длинным цилиндром на расстоянии r от нити или оси цилиндра:
 ,
,
где t – линейная плотность заряда.
· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
 ,
,
где s – поверхностная плотность заряда.
Напряженность поля между двумя равномерно и разноименно заряженными бесконечными параллельными плоскостями (поле плоского конденсатора)
 .
.
· Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью t, то на линии выделяется малый участок длиной dl с зарядом dq = t × dl. Такой заряд можно рассматривать как точечный и применять формулы:
 ;
;  ,
,
где  – радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
– радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность  и потенциал j поля, создаваемого распределенным зарядом:
и потенциал j поля, создаваемого распределенным зарядом:
 ;
;  .
.
Интегрирование ведется вдоль всей длины l заряженной линии (см. примеры 3 и 4).
· Связь потенциала с напряженностью:
а) в общем случае
 , или
, или  ;
;
б) в случае однородного поля
 ,
,
где d – расстояние между точками с потенциалами j 1 и j 2, взятое вдоль электрической силовой линии;
в) в случае поля, обладающего центральной или осевой симметрией  .
.
· Электрический момент диполя
 ,
,
где q – заряд;
 – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
· Работа сил поля по перемещению заряда q из точки поля с потенциалом j 1 в точку с потенциалом j 2
 , или
, или  ,
,
где Еl –проекция вектора напряженности  на направление перемещения;
на направление перемещения;
dl – величина перемещения.
В случае однородного поля
 ,
,
где l – величина перемещения;
a – угол между направлением вектора  и направлением перемещения
и направлением перемещения  .
.
· Электроемкость:
а) уединенного проводника
 ,
,
где j – потенциал проводника (при условии, что в бесконечности потенциал проводника равен нулю);
б) плоского конденсатора
 , или
, или  ,
,
где U – разность потенциалов пластин конденсатора;
S – площадь пластины (одной) конденсатора;
d – расстояние между пластинами;
в) уединенной проводящей сферы (шара) радиуса R
 .
.
· Электроемкость батареи конденсаторов:
а) при последовательном соединении
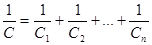 ,
,
б) при параллельном соединении:
С = С 1 + С 2 + …….+ Сn,
где n – число конденсаторов в батарее.
· Энергия заряженного уединенного проводника
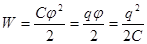 .
.
· Энергия заряженного конденсатора
 .
.
· Объемная плотность энергии электрического поля
 .
.
· Сила постоянного тока
 , или
, или  ,
,
где q, dq – заряд, прошедший через поперечное сечение проводника за время t, или dt.
· Плотность тока
 ,
,
где S – площадь поперечного сечения проводника.
· Связь плотности тока со средней скоростью  направленного движения заряженных частиц
направленного движения заряженных частиц
 ,
,
где q – заряд частицы;
n – концентрация заряженных частиц.
· Закон Ома:
а) для однородного участка цепи, не содержащего ЭДС
 ,
,
где  – разность потенциалов (напряжение) на концах участка цепи;
– разность потенциалов (напряжение) на концах участка цепи;
R – сопротивление участка;
б) для участка цепи, содержащего ЭДС
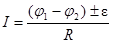 ,
,
где e – ЭДС источника тока на данном участке;
R – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
в) для замкнутой (полной) цепи
 ,
,
где R – внешнее сопротивление цепи;
r – внутреннее сопротивление источника тока с ЭДС e;
г) в дифференциальной форме
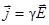 ,
,
где j – плотность тока;
g – удельная проводимость;
Е – напряженность электрического поля.
· Связь удельной проводимости g с подвижностью b заряженных частиц (ионов)
 ,
,
где qi – заряд иона;
n – концентрация ионов;
b+ и b- – подвижности положительных и отрицательных ионов.
· Сопротивление R и проводимость s однородного проводника длиной l и площадью поперечного сечения S:
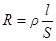 ;
;  ,
,
где r – удельное сопротивление проводника;
 – удельная проводимость проводника.
– удельная проводимость проводника.
Сопротивление проводника с переменным сечением вычисляется путем интегрирования выражения
 .
.
· Общее сопротивление системы проводников:
а)  – при последовательном соединении;
– при последовательном соединении;
б)  – при параллельном соединении,
– при параллельном соединении,
где Ri – сопротивление i -го проводника.
· Законы Кирхгофа:
а) первый закон:  ,
,
где 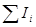 – алгебраическая сумма токов, сходящихся в узле;
– алгебраическая сумма токов, сходящихся в узле;
б) второй закон:  ,
,
где  – алгебраическая сумма произведений сил токов на сопротивления участков;
– алгебраическая сумма произведений сил токов на сопротивления участков;
 – алгебраическая сумма ЭДС, входящих в рассматриваемый замкнутый контур.
– алгебраическая сумма ЭДС, входящих в рассматриваемый замкнутый контур.
· Работа тока
а) для любого участка цепи:  ;
;
б) для участка, не содержащего Э.Д.С:  ,
,  .
.
· Мощность тока:  ;
; 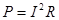 ;
; 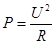 .
.
· Закон Джоуля-Ленца (тепловое действие тока в проводнике сопротивлением R за время прохождения тока t)
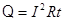 .
.
· Полная мощность, выделяющаяся в замкнутой цепи
 ,
,
где e – ЭДС источника тока.
Примеры решения задач
Пример 1. Три точечных заряда q 1 = q 2 = q 3 = 1 нКлрасположены в вершинах равностороннего треугольника. Какой заряд q 4нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии.
| Дано: | Решение: |
| q= q 2 = q 3 = 1 нКл | Все три заряда, расположенные по вершинам треугольника, находятся в оди- |
| Q 4-? |
|
 наковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например, q 1, находился в равновесии. Заряд q 1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рисунок 13):
наковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой-нибудь один из трех зарядов, например, q 1, находился в равновесии. Заряд q 1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рисунок 13):
 , (1)
, (1)
или 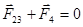 ,
,
где 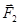 ,
,  ,
,  – силы, с которыми соответственно действуют на заряд q1, заряды q 2 ,q 3 ,q 4.
– силы, с которыми соответственно действуют на заряд q1, заряды q 2 ,q 3 ,q 4.
 – равнодействующая сил
– равнодействующая сил 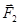 и
и  .
.
Так как силы  и
и  направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F 23– F 4 = 0, откуда F 4 = F 23.
направлены по одной прямой в противоположные стороны, то векторное равенство (1) можно заменить скалярным: F 23– F 4 = 0, откуда F 4 = F 23.
По закону Кулона  ,
,
где  ,
,  ,
,  .
.
 , так как q 1 = q 2 = q 3.
, так как q 1 = q 2 = q 3.
По теореме косинусов
 .
.
Так как  ,
,
то получим:  ,
,
или  , откуда
, откуда  .
.
Произведем вычисления:
 (Кл).
(Кл).
Ответ: q 4 = – 5,77 × 10-10 Кл. Следует отметить, что равновесие системы зарядов будет неустойчивым.
Пример 2. Определить напряженность электрического поля, созданного диполем, в точке на перпендикуляре к плечу диполя на расстоянии d =50 см от его центра, если заряды диполя q 1 = 10-8 Кл и q 2 = –10-8 Кл, а плечо диполя l = 5 см.
| Дано: | Решение: |
| d =50 см=0,5 м q 1 = 10-8 Кл q 2 = –10-8 Кл l =5 см=5×10-2 м | По принципу суперпозиции напряженность поля диполя в точке О равна сумме напряженностей Е от заряда q 1 и Е 2 от заряда q 2:  , или в проекциях на ось Ох: Е = Е 1 cos α + Е 2 cos α (рисунок 14). , или в проекциях на ось Ох: Е = Е 1 cos α + Е 2 cos α (рисунок 14).
|
| Е -? |
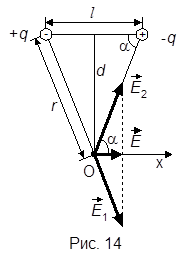
|
 Так как заряды диполя точечные, то
Так как заряды диполя точечные, то
 ,
,
Е = 2 Е 1 cos α.
Из рисунка находим
 ,
,
 .
.
Тогда

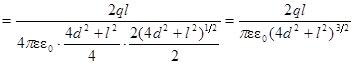 .
.
Так как l 2 << 4 d 2, то слагаемым l 2 можно пренебречь.
Следовательно,  .
.
Произведем вычисления:
 .
.
Ответ: Е = 36 В/м.
Пример 3. По тонкой нити, изогнутой по дуге окружности, равномерно распределен заряд с линейной плотностью t = 10 нКл/м. Определить напряженность  и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина нити составляет 1/3 длины окружности и равна l =15 см.
и потенциал j электрического поля, создаваемого таким распределенным зарядом в точке, совпадающей с центром кривизны дуги. Длина нити составляет 1/3 длины окружности и равна l =15 см.
| Дано: | Решение: |
| t =10 нКл/м=10-8 Кл/м l =15 см=0,15 м | Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а ось Оy была бы |
| Е -? j -? |
симметрично расположена относительно концов дуги (рисунок 15). На нити выделим элемент длины dl. Заряд dq = t × dl, находящийся на выделенном участке, можно считать точечным.
Определим напряженность электрического поля в точке О. Для этого найдем сначала напряженность  поля, создаваемого зарядом dq:
поля, создаваемого зарядом dq:
 ,
,
где  – радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность.
– радиус-вектор, направленный от элемента dl к точке, в которой вычисляется напряженность.
Выразим вектор  через проекции dEx и dEy на оси координат:
через проекции dEx и dEy на оси координат:
 ,
,
где  и
и  – единичные векторы направлений (орты).
– единичные векторы направлений (орты).
Напряженность  найдем интегрированием:
найдем интегрированием:
|
|
|
|
 .
.
Интегрирование ведется вдоль дуги длиной l. В силу симметрии  . Тогда
. Тогда
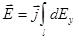 ,
,
где  .
.
Так как  ;
; 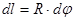 , то
, то
 .
.
Приняв во внимание симметричное расположение дуги относительно оси Оy, пределы интегрирования возьмем от 0 до  , а результат удвоим:
, а результат удвоим:

 .
.
Выразив радиус R через длину нити l ( Þ
Þ  ), получим:
), получим:  .
.
Из этой формулы видно, что напряженность  поля по направлению совпадает с осью Оу и численно равна:
поля по направлению совпадает с осью Оу и численно равна:
 .
.
Найдем потенциал электрического поля в точке О. Сначала найдем потенциал dj, создаваемый точечным зарядом dq в точке О:
 . Тогда:
. Тогда:
 ;
;
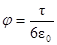 .
.
Произведем вычисления:
 .
.
 В.
В.
Ответ: Е = 2,18 кВ/м; j = 188 В.
Пример 4. На тонком стержне длиной l = 20 см равномерно распределен электрический заряд Q. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Найти линейную плотность t заряда на стержне.
| Дано: | Решение: |
| l =20 см=0,2 м a = 10 см=0,1 м q 1=40 нКл=4×10-8 Кл F =6 мкН=6×10-6 Н | Сила взаимодействия F заряженного стержня с точечным зарядом q 1 зависит от линейной плотности t заряда на стержне. Зная эту зависимость, можно определить t. Заряд на стержне |
| t -? |
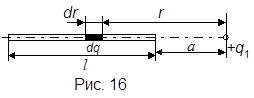
|
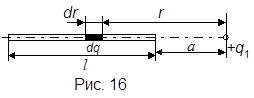 не является точечным, поэтому закон Кулона непосредственно применить нельзя. А если выделим из стержня малый участок dr с зарядом dq = t × dr (рисунок 16), который можно рассматривать как точечный, тогда по закону Кулона:
не является точечным, поэтому закон Кулона непосредственно применить нельзя. А если выделим из стержня малый участок dr с зарядом dq = t × dr (рисунок 16), который можно рассматривать как точечный, тогда по закону Кулона:
 .
.
Интегрируя это выражение в пределах от a до (a + l), получим:
 ;
;
откуда  .
.
Проверим, дает ли расчетная формула единицу линейной плотности электрического заряда.

 .
.
Найденная единица является единицей линейной плотности заряда.
Произведем вычисления:

 .
.
Ответ: t = 2,5 нКл/м.
Пример 5. В поле, созданном прямым бесконечно длинным цилиндром радиуса R =1 см и равномерно заряженным с поверхностной плотностью s =0,2 нКл/см2, находится точечный заряд q =25 нКл на расстоянии r =10 см от оси цилиндра. Найти силу, действующую на этот заряд.
| Дано: | Решение: |
| R =1 см=0,01 м s =0,2 нКл/см2=2×10-6 Кл/м2 q =25 нКл=25×10-8 Кл r =10 см=0,1 м | Сила, действующая на заряд q, находящийся в поле
 ,
где ,
где  – напряженность поля.
Напряженность поля беско- – напряженность поля.
Напряженность поля беско-
|
 -? -?
|
нечно длинного равномерно заряженного цилиндра
 ,
,
где t – линейная плотность заряда.
По определению
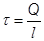 , а
, а 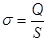 ,
,
где Q – заряд, равномерно распределенный по поверхности цилиндра.
Тогда Q = t× l =s × S =s × 2 pRl, откуда  .
.
Следовательно,
 , а
, а 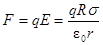 .
.
Произведем вычисления:
 .
.
Ответ: Сила  сонаправлена с напряженностью
сонаправлена с напряженностью  , которая в силу симметрии перпендикулярна поверхности цилиндра и равна F =565 мкН.
, которая в силу симметрии перпендикулярна поверхности цилиндра и равна F =565 мкН.
Пример 6. Электрическое поле создается двумя зарядами q 1= 4 мкКл и q 2= –2 мкКл, находящимся на расстоянии a =0,1 м друг от друга. Определить работу А 1-2 сил поля по перемещению заряда q =50 нКл из точки 1 в точку 2 (рисунок 17).
| Дано: | Решение: |
| q 1=4 мкКл=4×10-6 Кл q 2= –2 мкКл= –2×10-6 Кл а =0,1 м q =50 нКл=5×10-8 Кл | Для определения работы А 1-2 сил поля воспользуемся формулой А 1-2 = q (j 1– j 2 ), где j 1 и j 2 – потенциалы точек 1 и 2 поля. |
| A 1-2 -? |
По принципу суперпозиции электричеc  ких полей
ких полей
 ;
;
 .
.
Тогда
 .
.
Произведем вычисления:

=14,3×10-3 Дж=14,3 мДж.
Ответ: А 1-2 = 14,3 мДж.
Пример 7. Плоский воздушный конденсатор, расстояние между пластинами которого d 1=5 мм, подключен к источнику напряжения с ЭДС e=180 В. Площадь пластин конденсатора S =175 см2. Найти работу по раздвижению пластин до расстояния d 2=12 мм в двух случаях: 1) конденсатор перед раздвижением пластин отключен от источника: 2) конденсатор в процессе раздвижения пластин все время соединен с источником.
| Дано: | Решение: |
| d 1=5 мм=5×10-3 м e=180 В S=175 см2=1,75×10-2 м2 d 2=12 мм=12×10-3 м | 1) Работа, совершаемая при раздвижении пластин, после отключения конденсатора от источника напряжения A 1 = D W = W 2 - W 1, где W 1 – энергия заряженного конденсатора до раздвижения пластин; |
| A 1-? A 2-? |
W 2 – энергия конденсатора после раздвижения пластин.
Так как  , где q 1 – заряд и
, где q 1 – заряд и  – емкость конденсатора до раздвижения пластин, то:
– емкость конденсатора до раздвижения пластин, то:
 ;
;
аналогично, после раздвижения пластин
 .
.
Если конденсатор отключен от источника ЭДС, то заряд q на его пластинах остается постоянным в процессе раздвижения пластин. Следовательно,
 . Тогда:
. Тогда:
 .
.
 .
.
Произведем вычисления:
 =
=
= 705×10-9 Дж = 705 нДж.
2)Если конденсатор соединен с источником, то разность потенциалов на его пластинах остается постоянной, а заряд конденсатора изменяется. Полная работа, совершаемая при раздвижении пластин,
А = А 2 – Аист.,
где А 2 – работа внешней силы;
Аист = e×D q =e (q 1 – q 2) – работа источника по перемещению заряда D q;
q 1 = С 1 × e – заряд конденсатора до раздвижения пластин;
q 2 = С 2 × e – заряд конденсатора после раздвижения пластин.
Работу источника Аист мы взяли со знаком минус, так как при перемещении заряда с положительной обкладки на отрицательную источник совершает отрицательную работу.
Иначе, полная работа равна изменению энергии конденсатора:
А = D W = W 2 – W 1.
Тогда получим: А 2 – Аист = W 2 – W 1, откуда
А 2 = W 2 – W 1 + Аист.
Здесь  и
и  – энергия конденсатора до и после раздвижения пластин.
– энергия конденсатора до и после раздвижения пластин.


Следовательно,
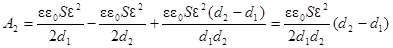 ;
;
 .
.
Произведем вычисления:

= 293 × 10-9 Дж = 293 нДж.
Ответ: А 1 = 705 нДж; А 2 = 293 нДж.
|
| Дано: | Решение: |
| R =50 Ом Uо =2 В U =5 В t =15 с | Так как сила тока в проводнике изменяется со временем, то заряд, прошедший по проводнику  , где t 1=0, t 2= t. , где t 1=0, t 2= t.
|
| q -? | |
По закону Ома  , тогда
, тогда  .
.
Так как напряжение со временем равномерно нарастает, то оно может быть выражено формулой
U = Uo + Kt,
где K – коэффициент пропорциональности.
У нас 
Тогда 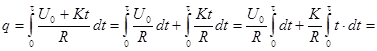

Подставив числовые значения, получим:
 (Кл).
(Кл).
Ответ: q = 1,05 Кл.
Пример 9. Определить ЭДС 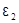 второго элемента в цепи (рис.18), если
второго элемента в цепи (рис.18), если  =2 В, R 1=100 Ом, R 2=50 Ом, R 3=20 Ом. Гальванометр регистрирует силу тока I 3=50 мА, идущего в направлении, указанном стрелкой. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
=2 В, R 1=100 Ом, R 2=50 Ом, R 3=20 Ом. Гальванометр регистрирует силу тока I 3=50 мА, идущего в направлении, указанном стрелкой. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.
| Дано: | Решение: |
 =2 В
R 1=100 Ом
R 2=50 Ом
R 3=20 Ом
I 3=50мА=5×10-2A =2 В
R 1=100 Ом
R 2=50 Ом
R 3=20 Ом
I 3=50мА=5×10-2A
| Выберем направление токов I 1, I 2, I 3 через сопротивления R 1, R 2, R 3. По первому закону Кирхгофа для узла В имеем: I 1 – I 2 – I 3 = 0.
По второму закону Кирхгофа имеем:
- для контура I (ABC  A) A)  ;
- для контура II (ABD ;
- для контура II (ABD 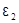 A) A)  . .
|
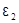 -? -?
|
 После подстановки числовых значений в полученные формулы получим систему уравнений:
После подстановки числовых значений в полученные формулы получим систему уравнений:
 ,
,
|
 .
.
Так как требуется определить только одно неизвестное 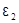 из трех, то воспользуемся методом определителей. Составим и вычислим определитель D системы:
из трех, то воспользуемся методом определителей. Составим и вычислим определитель D системы:
 Составим и вычислим определитель D
Составим и вычислим определитель D 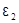 :
:

 .
.
Числовое значение ЭДС: 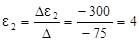 В.
В.
Ответ: 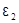 = 4 В.
= 4 В.
Пример 10. Батарея состоит из n =5 последовательно соединенных элементов, каждый с ЭДС  =1,4 В и внутренним сопротивлением ri =0,3 Ом. При каком токе полезная мощность батареи Рn =8 Вт? Найти наибольшую полезную мощность батареи.
=1,4 В и внутренним сопротивлением ri =0,3 Ом. При каком токе полезная мощность батареи Рn =8 Вт? Найти наибольшую полезную мощность батареи.
| Дано: | Решение: |
n =5
 =1,4 В
ri =0,3 Ом
Рn =8 Вт =1,4 В
ri =0,3 Ом
Рn =8 Вт
| Полезная мощность батареи Pn = I2R, где R – сопротивление внешней цепи; I – сила тока в цепи, которая определяется по закону Ома: |
| I -? Рn max-? |
 (n – число элементов в батарее).
(n – число элементов в батарее).
Так как  , то получим:
, то получим: 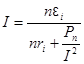 , или
, или  ;
;
 ;
;  .
.
Решая это квадратное уравнение, найдем:
 .
.
Подставляя числовые значения, получим:
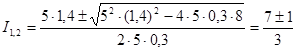 ;
;
I 1 = 2,67 A; I 2 = 2 А.
Полезная мощность, выделяемая во внешней части цепи:
 .
.
Эта мощность будет максимальной при выполнении условия:  ,
,
или 


 ;
; 
Подставляя найденное значение R max в формулу  , получим:
, получим:
 ;
;
 (Вт).
(Вт).
Ответ: I 1 = 2,7 А; I 2 = 2 А; Рn max = 8,2 Вт.
Пример 11. Сила тока в проводнике сопротивлением 20 Ом равномерно нарастает за D t =2с от I 0=0 до I =6 А. Определить количество теплоты, выделившейся в проводнике за первые три секунды.
| Дано: | Решение: |
| R =20 Ом D t =2с I 0=0 I =6 А t =3 с | По закону Джоуля-Ленца dQ = I2Rdt (1) Так как сила тока является функцией времени, то I=Kt, (2) где K – коэффициент пропорциональности, численно равный приращению тока в единицу времени: |
| Q -? |
 .
.
С учетом (2) формула (1) примет вид:
dQ = K2Rt2dt.
За первые t =3 с выделится количество теплоты:
 .
.
Произведем вычисления:  (Дж).
(Дж).
Ответ: Q=1620 Дж.
Пример 12. Определить концентрацию дырок в полупроводнике германия при такой температуре, когда его удельное сопротивление ρ =0,5 Ом×м, если подвижности электронов и дырок соответственно равны bn =0,40 м2/В×с; bр =0,20 м2/В×с.
| Дано: | Решение: |
| ρ =0,5 Ом×м bn =0,40 м2/В×с bр =0,20 м2/В×с | Удельная проводимость собственных полупроводников равна: γ = en (bn + bр), где bп и bр – подвижности электронов и дырок соответственно; |
| n -? |
e – заряд электрона;
п – концентрация свободных электронов, т.е. число их в единице объема.
В собственном полупроводнике концентрация дырок равна концентрации свободных электронов.
Так как  , то получим:
, то получим:
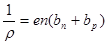 , откуда
, откуда 
Подставив числовые значения величины, найдем:

Ответ: п = 2,08 ∙ 1019 м -3.
К о н т р о л ь н а я р а б о т а № 2
| Вар. | Номера задач | |||||||
К о н т р о л ь н а я р а б о т а № 2 а
| Вар. | Номера задач | |||||||||
201. Три одинаковых точечных заряда q 1 =q 2 =q 3=2 нКл находятся в вершинах равностороннего треугольника со сторонами a =10 см. Определить модуль и направление силы  , действующей на один из зарядов со стороны двух других.
, действующей на один из зарядов со стороны двух других.
202. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Шарики погружают в масло. Найти плотность ρ масла, если угол расхождения нитей при погружении шариков в масло остается неизменным. Плотность материала шариков ρо =1,5×103 кг/м3, диэлектрическая проницаемость масла ε = 2,2.
203. Точечные заряды q 1=30 мкКл и q 2= –20 мкКл находятся на расстоянии d =20 см друг от друга. Определить напряженность электрического поля  в точке, удаленной от первого заряда на расстояние r 1=30 см, а от второго – на r 2= 15 см.
в точке, удаленной от первого заряда на расстояние r 1=30 см, а от второго – на r 2= 15 см.
204. Четыре одинаковых заряда q 1 =q 2 =q 3 =q 4=40 нКл закреплены в вершинах квадрата со стороной а =10 см. Найти силу  , действующую на один из этих зарядов со стороны трех остальных.
, действующую на один из этих зарядов со стороны трех остальных.
205. Точечные заряды q 1=20 мкКл и q 2= –10 мкКл находятся на расстоянии d =5 см друг от друга. Определить напряженность поля в точке, удаленной на расстояние r 1=3 см от первого и на расстояние r 2= 4 см от второго заряда. Найти также силу  , действующую в этой точке на точечный заряд q =1 мкКл.
, действующую в этой точке на точечный заряд q =1 мкКл.
206. В вершинах квадрата находятся одинаковые заряды q 1 =q 2 = q 3 =q 4= 8×10-10 Кл. Какой отрицательный заряд q нужно поместить в центре квадрата, чтобы система находилась в равновесии?
207. Два одинаковых положительных заряда q 1 =q 2 = 0,1 мкКл находятся в воздухе на расстоянии а =8 см друг от друга. Определить напряженность поля в точке О, находящейся на середине отрезка, соединяющего заряды, и в точке A, расположенной на расстоянии r =5 см от зарядов.
208. На расстоянии d =20 см друг от друга расположены два точечных заряда: q 1= –50 нКл и q 2=100 нКл. Определить силу  , действующую на заряд q 3= –10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
, действующую на заряд q 3= –10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
209. Два шарика массой m =1 г каждый подвешены на нитях в одной точке. Длина каждой нити l =10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол a= 60°?
210. Два небольших одинаковых шарика массой m = 0,1 г каждый подвешенный в одной точке на нитях одинаковой длины l =25 см. После того, как шарикам были сообщены одинаковые заряды, они разошлись на расстояние r =5 см друг от друга. Найти заряд каждого шарика.
211. Тонкий стержень длиной l =20 см несет равномерно распределенный заряд с линейной плотностью τ =0,1 мкКл/м. Определить напряженность  электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.
электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.
212. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью τ = 0,5 мкКл/м. Определить напряженность  электрического поля, создаваемого распределенным зарядом в точке A, лежащей на оси стержня на расстоянии 15 см от его начала.
электрического поля, создаваемого распределенным зарядом в точке A, лежащей на оси стержня на расстоянии 15 см от его начала.
213. По тонкому кольцу радиусом R =10 см равномерно распределен заряд Q =20 мкКл. Определить потенциал φ электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстоянии а =20 cм от центра кольца.
214. По тонкому полукольцу равномерно распределен заряд с линейной плотностью τ =0,2 мкКл/м. Определить потенциал электростатического поля в точке, лежащей на оси полукольца и удаленной от его центра на расстояние, равное радиусу полукольца.
215. На продолжении оси тонкого прямого стержня, равномерно заряженного с линейной плотностью заряда τ = 15 нКл/см на расстоянии а =40 см от конца стержня находится точечный заряд q =10 мкКл. Второй конец стержня уходит в бесконечность. Определить силу, действующую на заряд q.
216. Тонкий стержень согнут в кольцо радиусом r =5 см. Он равномерно заряжен с линейной плотностью τ =800 нКл/см. Определить потенциал φ в точке, расположенной на оси кольца на расстоянии h =10см от его центра.
217. Тонкостенный бесконечно длинный цилиндр диаметром d =10 см равномерно заряжен с поверхностной плотностью заряда s = 4 мкКл/м2. Найти напряженность поля в точке, отстоящей от поверхности цилиндра на расстоянии а = 15см.

|
218. Электростатическое поле создано зарядами q 1=2мкКл и q 2 = –2 мкКл, находящимися на расстоянии а =10 см друг от друга. Определить работу сил поля, совершаемую при перемещении заряда q = 0,5 мкКл из точки 1 в точку 2 (рис. 19).
219. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой τ =20 нКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстояние r 1 = 10 см и r 2 = 15 см.
220. Поле образовано точечным диполем с электрическим моментом р = 200 пКл×м. Определить разность потенциалов U двух точек поля, расположенных симметрично относительно диполя на его оси на расстоянии r = 40 см от центра диполя.
221. Узкий пучок электронов, обладающих скоростью  =2×104 км/с, проходит в вакууме посередине между обкладками плоского конденсатора. Какую наименьшую разность потенциалов нужно приложить к пластинам, чтобы электроны не вышли из конденсатора? Расстояние между пластинами d = 1 см, длина их l = 3 см.
=2×104 км/с, проходит в вакууме посередине между обкладками плоского конденсатора. Какую наименьшую разность потенциалов нужно приложить к пластинам, чтобы электроны не вышли из конденсатора? Расстояние между пластинами d = 1 см, длина их l = 3 см.
222. Точечный заряд q = 10-8 Кл находится на расстоянии l = 50 см от поверхности шара радиусом R = 9 см и заряженного до потенциала φш = 25 кВ. Какую работу надо совершить для уменьшения расстояния между шаром и зарядом до l 2 = 20 см?
223. В центре полого металлического шара радиусом R = 1 м с зарядом q = 3,35 нКл находится маленький шарик с зарядом qо = 6,68 нКл. Определить потенциалы и напряженность поля в точках, находящихся от центра шара на расстояниях l = 0,5; 1; 10 м.
224. Электрон, летевший горизонтально со скоростью  = 1500 км/с, влетел в однородное электрическое поле с напряженностью Е = 100 В/см, направленное вертикально вверх. Какова будет по величине и направлению скорость электрона через t = 10-9 с?
= 1500 км/с, влетел в однородное электрическое поле с напряженностью Е = 100 В/см, направленное вертикально вверх. Какова будет по величине и направлению скорость электрона через t = 10-9 с?
225. Протон, начальная скорость которого  = 2×105 м/с, влетает в однородное электрическое поле (Е = 300 В/см) так, что вектор скорости совпал с направлением линий напряженности. Какой путь должен пройти протон в направлении линий поля, чтобы его скорость удвоилась?
= 2×105 м/с, влетает в однородное электрическое поле (Е = 300 В/см) так, что вектор скорости совпал с направлением линий напряженности. Какой путь должен пройти протон в направлении линий поля, чтобы его скорость удвоилась?
226. По направлению силовой линии электрического поля, созданного бесконечной плоскостью, заряженной отрицательно с поверхностной плотностью s = 2,54×10-2 мкКл/м2, летит электрон. Определить минимальное расстояние, на которое может подойти к плоскости электрон, если на расстоянии lo = 5 см он имел кинетическую энергию Т = 60 эВ.
227. Пучок электронов направлен параллельно пластинам плоского конденсатора длиной l = 5 см с расстоянием между пластинами d = 3 см. С какой скоростью влетели электроны в конденсатор, если известно, что они отклонились за время полета в конденсаторе на х = 3 мм? Разность потенциалов между пластинами U = 700 В. Определить кинетическую энергию электронов.
228. Определить потенциал в начальной точке перемещения заряда q 1 = –6×10-8 Кл, движущегося в поле заряда q2 = +4×10-8 Кл, если энергия, затраченная на перемещение заряда Е = 6×10-5 Дж, а потенциал конечной точки j 2 = 1500 В. Установить, на каком расстоянии находились заряды в начале и в конце перемещения.
 229. Какой минимальной скоростью
229. Какой минимальной скоростью  min должен обладать протон, находящийся на расстоянии l = 3 R от поверхности металлического шара радиуса R и заряженного до потенциала j = 400 В, чтобы он мог достигнуть поверхности шара?
min должен обладать протон, находящийся на расстоянии l = 3 R от поверхности металлического шара радиуса R и заряженного до потенциала j = 400 В, чтобы он мог достигнуть поверхности шара?
230. Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (t = 10 нКл/м). Определить кинетическую энергию Т 2 электрона в точке 2, если в
точке 1 его кинетическая энергия <







