Пример 3. Мяч бросили вертикально вверх со скоростью 
o = 50м/с, а спустя t = 1 с из того же места, в том же направлении и с той же скоростью бросили второй мяч. Когда и где встретятся мячи? Какова будет их скорость в момент встречи? Как со временем изменяется расстояние между мячами и скорость второго мяча относительно первого?
| Дано: | Решение: |
| o = 50 м/с
t = 1
| За начало системы координат примем точку бросания мячей, ось О х направим вертикально вверх. Для наглядности законы движения тел изобразим графически (рисунок 4). Запишем уравнения для координат первого и второго мяча в любой момент времени t: |
| tв -? h -?
1в -? 2в -?
D x -? от -?
|
;
В момент встречи tв координаты мячей равны, т.е. х1 = х2 или
Решим это уравнение относительно tв:
;
;
, где g = 9,8 м/с2.
Подставляя это значение tв в уравнение для х1 или х2, получим:
В любой момент времени t скорости мячей 
и 
.
В момент встречи мячей их скорости будут
= 50 м/с – 9,8 м/с2 × 5,6 с = – 4,9 м/с,
= 50-9,8×(5,6-1) = 4,9 (м/с).
Оба мяча имеют одинаковые по модулю скорости, но направленные навстречу друг другу. Первый мяч падает, второй – поднимается вверх.
В любой момент времени t расстояние между мячами
.
Скорость второго мяча относительно первого
от = 
– 
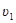= o– g (t –t) – ( o– gt) = o– gt + g t – o+ gt = g t = const
от = 9,8 м/с2 × 1 с = 9,8 м/с
Ответ: tв»5,6 с; h = 126,1 м; 
= – 4,9 м/с; 
= 4,9 м/с;
D х = 
g t2+ o t– g t t; от = 9,8 м/с = const.
Пример 4. На железнодорожной платформе, движущейся со скоростью = 36 км/ч, укреплено орудие, ствол которого направлен в сторону движения платформы и приподнят над горизонтом на угол a = 45о. Орудие произвело выстрел, в результате чего скорость платформы уменьшилась в n = 2 раза. Найти скорость u снаряда (относительно орудия) при вылете из ствола. Масса снаряда m = 40 кг, масса платформы с орудием (без снаряда) M = 1,5 т.
| Дано: | Решение: |
| = 36 км/ч = 10 м/с
a = 45о
n = 2
m = 40 кг
M = 1,5 т = 1500 кг
| На систему платформа с орудием – снаряд извне действуют две силы: тяжести (m+M)  и реакции  рельсов. До выстрела эти силы уравновешивались, так как система двигалась равномерно. Во время выстрела сила взаимодействия между платформой и рельсами возрастает вследствие явления отдачи, поэтому равновесие сил,
|
| u -? |
приложенных к системе, нарушается: N >(m+M) g. Следовательно, во время выстрела система не является замкнутой, ее импульс изменяется. Однако следует учесть, что обе рассмотренные силы действуют по вертикали, в то время как в горизонтальном направлении никакие силы на систему не действуют (трением колес платформы о рельсы пренебрегаем). Поэтому проекция импульса системы на горизонтальное направление (направление движения платформы) есть величина постоянная. Рассматривая все движения относительно поверхности земли, получим:
, (1)
где с cos b – проекция на ось О х скорости с снаряда относительно Земли (рисунок 5).
Чтобы связать скорость с с искомой скоростью u, будем рассматривать движение снаряда относительно Земли как сложное, состоящее из двух: со скоростью u относительно орудия и со скоростью 
вместе с орудием относительно Земли. Тогда 
.
Перепишем это уравнение в проекции на ось О х:
.
Тогда уравнение (1) примет вид:
;
;
; 
.
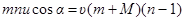Произведем вычисления:
м/с = 272,3 м/с.
Ответ: u = 272,3 м/с.
Пример 5. При выстреле из пружинного пистолета вертикально вверх пуля массой m = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на x = 10 см. Массой пружины и силами трения пренебречь.
| Дано: | Решение: |
| m = 20 г = 0,02 кг h = 5 м x = 10 см = 0,1 см | Рассмотрим систему пружина – пуля. Так как на тела системы действуют только консервативные силы, то для решения задачи можно применить закон сохранения энергии в механике. Согласно ему полная механическая энергия Е1 системы в начальном состоя- |
| h -? |
нии (в данном случае перед выстрелом) равна полной энергии Е2 в конечном состоянии (когда пуля поднялась на высоту h), т.е.
Е1 = Е2, или Т1 +П1 = Т2 + П2, (1)
где Т1, Т2, П1 и П2 – кинетические и потенциальные энергии системы в начальном и конечном состояниях.
Так как кинетические энергии пули в начальном и конечном состояниях равны нулю, то равенство (1) примет вид:
П1 = П2 (2)
Примем потенциальную энергию пули в поле тяготения Земли, когда пуля покоится на сжатой пружине, равной нулю, а высоту подъема пули будем отсчитывать от торца сжатой пружины. Тогда энергия системы в начальном состоянии будет равна потенциальной энергии сжатой пружины, т.е. П1 = 
kx2, а в конечном состоянии – потенциальной энергии пули на высоте h, т.е. П2 = mgh. Подставив выражения П1 и П2 в формулу (2), найдем kx2 = mgh, откуда
(3)
Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (3) вместо величин подставим их единицы:
.
Убедившись, что полученная единица является единицей жесткости (1Н/м), подставим в формулу (3) значения величин и произведем вычисления:
.
Ответ: k = 196 H/м.
Пример 6. На горизонтальную ось насажен шкив радиуса R = 10 см. На шкив намотан шнур, к свободному концу которого подвесили гирю массой m = 0,5 кг. Масса шкива М = 2 кг. Считая массу шкива равномерно распределенной по ободу, определить ускорение a, с которым будет опускаться гиря, силу натяжения Т нити и силу давления N шкива на ось.
| Дано: | Решение: |
| R = 10 см = 0,1 м m = 0,5 кг М = 2 кг g = 9,8 м/с2 | Поскольку ускорение центра инерции шкива a c = 0 и шкив только вращается, уравнения движения шкива запишутся в виде
а)  , б)  (1)
На шкив действуют сила тяжести  ,
|
| а -? T -? N -? |
сила натяжения 
нити и сила реакции 
оси. Последняя по третьему закону Ньютона численно равна искомой силе давления шкива на ось. Сила направлена вертикально вверх. Уравнение (1,а) в проекциях на ось Ох имеет вид:
Mg+T-N = 0. (2)
Шкив вращается под действием лишь момента силы Т. Следовательно, уравнение (1,б) дает:
TR = I e. (3)
Момент инерции шкива, поскольку его масса равномерно распределена по ободу, найдем по формуле:
I = MR2 (4)
Уравнения (2) и (3), описывающие движение шкива, содержат три неизвестных: T, N и e. Недостающее уравнение запишем, применив второй закон Ньютона для поступательного движения гири (в проекциях на ось Ох):
mg-T = ma (5)
Так как шнур сматывается со шкива без проскальзывания, то ускорение гири равно линейному ускорению точек на ободе шкива. Следовательно, угловое ускорение шкива
(6)
Подставив в (3) значения I, e по формулам (4) и (6), получим:
T = Ma (7)
Решая систему уравнений (2), (5), (7), найдем все три неизвестные величины:
; 
; 
.
Произведем вычисления:
.
.
.
Ответ: a = 1,96 м/с2; Т = 3,92 Н; N = 23,54 H.
Пример 7. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол j повернется платформа, если человек пойдет вдоль края платформы и, обойдя ее, вернется в исходную (на платформе) точку? Масса платформы m1 = 280 кг, масса человека m2 = 80 кг. Момент инерции человека рассчитывать как для материальной точки.
| Дано: | Решение: |
| m1 =280 кг m2 = 80 кг | Перемещаясь по платформе, человек взаимодействует с ней. Согласно условию задачи, момент внешних сил относительно оси вращения, совпадающей с геометрической осью платформы, мо- |
| j -? |
жно считать равной нулю. Следовательно, для системы платформа – человек выполняется закон сохранения момента импульса, который запишем так:
,
где 
– момент импульса системы в начальном состоянии,
– момент импульса системы в конечном состоянии.
Следовательно,
, (1)
где I1 и I2 – моменты инерции платформы и человека относительно оси, проходящей через центр платформы в начальный момент (человек стоит на краю платформы).
Момент инерции платформы
,
где R – радиус платформы.
Момент инерции человека относительно центра платформы
.
w0 – начальная угловая скорость платформы и человека (w0 = 0).
– момент инерции платформы с человеком:
.
w1 – конечная угловая скорость платформы с человеком. w2 – конечная угловая скорость человека.
За время D t обхода человеком края платформы платформа повернется на угол j, а сам человек – на угол (2 p - j). Следовательно, угловая скорость человека 
, а платформы с человеком 
, так как платформа вращается в противоположную сторону движения человека (назад). Тогда уравнение (1) примет вид:
,
или 
.
,
.
Произведем вычисления:
рад = 96°
Ответ: j = 96о.
Пример 8. Какую минимальную работу нужно совершить, чтобы забросить тело массой 
= 1000 кг с поверхности Земли на Луну? Расстояние между центрами Земли и Луны равно 60 радиусам Земли. Масса М Земли больше массы m Луны в 81 раз. Считать, что при перемещении тела взаимное положение Луны и Земли не меняется. Сопротивление воздуха не учитывать.
| Дано: | Решение: |
| = 1000 кг
l = 60 Rз
Mз = 81 mл
| Тело массой необходимо перемещать все время в суммарном гравитационном поле Земли и Луны. На прямой, соединяющей центры Земли и Луны, есть точка С (рисунок 8), в которой гравитационные поля Земли и Луны
|
| Аmin -? |
уравновешиваются (s з = s л). Точка С делит весь путь тела 
на две части. На первом участке от Земли до точки С сила тяготения суммарного гравитационного поля Земли и Луны направлена к Земле, на втором участке от точки С до Луны – к Луне.
Очевидно, на первом участке необходимо совершать работу против сил тяготения, а на втором участке – не обязательно, так как достигнув точки С с любой, сколь угодно малой скоростью, тело тут же начнет двигаться ускоренно к Луне под действием сил тяготения.
Следовательно, работа будет минимальной, если тело достигнет точки С с минимальной скоростью, необходимой для дальнейшего движения. Эту скорость, а значит, и кинетическую энергию тела в точке С можно считать равной нулю.
Таким образом, работа пойдет только на увеличение потенциальной энергии тела в суммарном поле тяготения Земли и Луны. Поэтому она может быть вычислена по формуле
A = - m ¢(j1-j2) = m ¢(j2-j1), (1)
где j1 и j2 – потенциалы гравитационного поля у поверхности Земли и в точке С соответственно.
Из принципа суперпозиции (наложения) полей следует, что потенциал в каждой точке пространства
j = jз+jл (2)
где jз и jл - потенциалы полей тяготения Земли и Луны в этой точке.
Так как потенциал поля, созданного материальной точкой массой m на расстоянии r от нее, равен:
, то получим 
,
или 
.
,
где х – расстояние от центра Земли до точки С.
Поскольку модули векторов напряженности гравитационных полей Земли и Луны в точке С равны: sз = s л, то получим:
, или 
Решив эти уравнения, найдем: х1 = 54 RЗ; х2 = 67,5 RЗ.
Корень х2 >67,5 RЗ не удовлетворяет условию задачи. Следовательно, х1 = 54 RЗ. Тогда
Подставив значения потенциалов j1 и j2 в формулу (1), получим:
;
Так как ускорение силы тяжести на Земле 
м/с2, то получим: 
, где RЗ = 6,37×106 м – радиус Земли.
Произведем вычисления:
A min = 0,98 × 9,81 × 6,37 × 106 × 103 Дж = 61,2 × 109 Дж.
Ответ: A min = 61,2 × 109 Дж.
Пример 9. Материальная точка массой 20 г совершает гармонические колебания с периодом 2 сек. Определить амплитуду колебаний, максимальные скорость и ускорение колеблющейся точки, если максимальная кинетическая энергия ее равна 0,05 Дж.
| Дано: | Решение: |
| m =20 г = 0,02 кг Т = 2 с Ек max = 0,05 Дж | Полная энергия колеблющейся точки массой m равна Еk max: Е = Еk max = m w2 A 2, где w =  . Откуда амплитуда
|
| А -? max-? a max-?
|
, или 
.
Уравнение гармонических колебаний точки x = A sin(w t + j o).
Скорость точки 
, где амплитуда скорости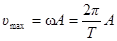 
.
Ускорение колеблющейся точки
,
где амплитуда ускорения 
. 
Максимальную скорость точки можно найти из уравнения
Ек max = m 
, откуда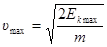 
.
Произведем вычисления:
.
.
.
.
Ответ: А = 0,71 м; = 2,23 м/с;
= 7 м/с2.
Пример 10. На верхнем конце тонкого стержня длиной 30 см и массой 100 г укреплен маленький шарик (материальная точка) массой 20 г, на нижнем – шарик радиусом 5 см и массой 180 г. Определить период колебаний стержня с шариками около горизонтальной оси, проходящей через точку О в центре стержня (рисунок 9).
| Дано: | Решение: |
| l = 30 см = 0,3 м mст = 100 г = 0,1 кг m = 20 г = 0,02 кг R = 5 см = 0,05 м М = 180 г = 0,18 кг | Период колебаний физического маятника, каким является стержень с шариками, определяется по формуле:
 ,
где I – момент инерции маятника;
mобщ – масса маятника;
|
| Т -? |
а – расстояние от центра тяжести (центра масс) маятника до оси вращения.
Момент инерции физического маятника I состоит из моментов инерции I1 и I2 обоих шариков и момента инерции I3 стержня: I = I1+I2+I3.
Момент инерции верхнего шарика 
;
момент инерции нижнего шарика (по теореме Штейнера) I2 = Iш+Mr2 = 
MR2+M 
; момент инерции стержня относительно оси, проходящей через его середину I3 = 
mстl 2. Общий момент инерции физического маятника: 
.
Масса маятника
mобщ = mст+m+M.
Для определения расстояния а напишем условие равновесия стержня с шариками, находящегося в горизонтальном положении, относительно центра тяжести (рисунок 10).
