При решении физических задач числовые значения, с которыми приходится иметь дело, большей частью являются приближенными. Задачи с приближенными данными нужно решать с соблюдением правил подсчета значащих цифр. Значащими называются все цифры, кроме нуля, а также и нуль в двух случаях: 1) когда он стоит между значащими цифрами; 2) когда он стоит в конце числа и когда известно, что единицы соответствующего разряда в данном числе нет.
Приближенные вычисления следует вести с соблюдением следующих правил:
1. Так как с помощью вычислений получить результат более точный, чем исходные данные, невозможно, то достаточно производить вычисления с числами, содержащими не больше знаков, чем в исходных данных.
|
2. При сложении или вычитании приближенных чисел, имеющих различную точность, более точное число должно быть округлено до точности менее точного. Например:
9,6 + 0,176 = 9,6 + 0,2 = 9,8;
100,8 - 0,425 = 100,8 - 0,4 = 100,4.
3. При умножении и делении следует в полученном результате сохранять столько значащих цифр, сколько их имеет приближенное число с наименьшим количеством значащих цифр. Например:
0,637 × 0,23 × 5,2 = 0,76, но не 0,761852;
6,32:3 = 2, но не 2,107.
4. При возведении в квадрат или в куб нужно сохранять столько значащих цифр, сколько их имеется в основании степени. Например:
1,232 = 1,51, но не 1,5129;
3,013 = 27,3, но не 27,270901.
5. При извлечении квадратного или кубического корня в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число. Например:
= 1,09 × 10-3, но не 1,09087 × 10-3;
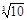= 2,1, но не 2,154.
6. При вычислении сложных выражений соблюдаются указанные правила в зависимости от вида производимых действий. В промежуточных результатах следует сохранять на одну значащую цифру больше. Например: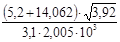 
.
Сомножитель 3,1 имеет наименьшее число значащих цифр – две. Поэтому результаты всех промежуточных вычислений должны округляться до трех значащих цифр:
После округления результата до двух значащих цифр получаем 6,1×10-3.
7. Если число незначительно отличается от единицы, можно пользоваться приближенными формулами.
Если а, b, с много меньше единицы (меньше 0,05), то можно принимать:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
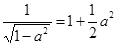
8) 
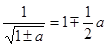
9) 
10) 
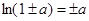
11) 
8. Если угол a<<5° и выражен в радианах, то в первом приближении можно принять: 
; 
.
Соблюдая эти правила, студент сэкономит время на вычислении искомых величин при решении физических задач.
УЧЕБНЫЕ МАТЕРИАЛЫ
ПО РАЗДЕЛАМ КУРСА ФИЗИКИ
ФИЗИЧЕСКИЕ ОСНОВЫ
КЛАССИЧЕСКОЙ МЕХАНИКИ
Основные законы и формулы
· Средняя путевая скорость и среднее ускорение
; 
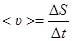где D S - путь, пройденный точкой за интервал времени D t.
Путь D S в отличие от разности координат D x = x2 – x1 не может убывать и принимать отрицательные значения, т.е. D S ³0.
· Мгновенная скорость и мгновенное ускорение
или 
;
· Тангенциальная и нормальная составляющая ускорения
; 
,
где R – радиус кривизны траектории.
· Полное ускорение
; 
· Кинематическое уравнение равнопеременного движения материальной точки (центра масс твердого тела) вдоль оси X
,
где хо – начальная координата движущейся точки в момент времени t = 0;
ox – проекция скорости точки на ось Х в этот момент
времени;
ax – проекция мгновенного ускорения на ось Х.
· Скорость и путь равнопеременного поступательного движения
· Угловая скорость и угловое ускорение
; 
.
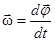· Кинематические уравнения равнопеременного вращательного движения
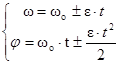
· Связь между линейными и угловыми величинами при вращательном движении: длина дуги, пройденная точкой
,
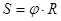где j – угол поворота тела,
R – радиус вращения точки;
; 
; 
.
· Импульс (количество движения) материальной точки массой m, движущейся со скоростью 
,
.
· Основное уравнение динамики поступательного движения (второй закон Ньютона)
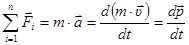
· Силы, рассматриваемые в механике:
а) сила упругости
,
где k – коэффициент упругости;
x – абсолютная деформация;
б) сила трения скольжения
,
где f – коэффициент трения;
N – сила нормального давления;
в) сила гравитационного взаимодействия (сила тяготения)
,
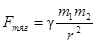где g – гравитационная постоянная;
m1 и m2 – массы взаимодействующих тел;
r – расстояние между телами (тела рассматриваются как материальные точки);
г) сила, действующая на тело, движущееся по дуге окружности радиуса R
.
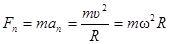· Закон сохранения импульса (количества движения) для замкнутой (изолированной) системы
,
или для двух тел (i = 2):
,
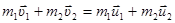где 
и 
– скорости тел в начальный момент времени (до взаимодействия);
и 
– скорости тех же тел после их взаимодействия.
· Кинетическая энергия тела, движущегося поступательно
, или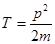 
.
· Потенциальная энергия:
а) упругодеформированного тела
,
где k – коэффициент упругости (жесткость) тела;
x – абсолютная деформация;
б) гравитационного взаимодействия тел
;
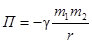в) тела, поднятого над поверхностью Земли
,
где g – ускорение свободного падения;
h – высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<RЗ, где RЗ – радиус Земли).
· Закон сохранения полной механической энергии (для замкнутой системы)
Е = Т+П = const.
· Работа А, совершаемая внешними силами, определяется как мера изменения энергии системы (тела): A = D Е = Е2 - Е1
· Работа:
а) постоянной силы F:
,
где a - угол между направлениями силы 
и перемещения 
;
б) переменной силы F:
dS
где a и b – координаты начальной и конечной точек пути;
в) упругой силы
.
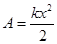· Мощность:
а) средняя за время D t
;
б) мгновенная
, или 
.
· Напряженность гравитационного поля Земли
, или 
,
где МЗ – масса Земли;
RЗ – радиус Земли;
h – высота над поверхностью Земли.
· Потенциал гравитационного поля Земли
, или 
.
· Момент инерции материальной точки
,
где r – радиус (расстояние от точки до оси вращения).
· Момент инерции системы (тела)
, или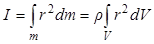 
,
где dm – элементарная масса тела;
dV – элементарный объем тела;
r – плотность вещества тела.
· Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс (центр симметрии):
а) полого (тонкостенного) и сплошного цилиндров (или диска) радиуса R
; 
;
б) шара радиуса R
;
в) тонкого стержня длиной l, если ось вращения перпендикулярна стержню
;
то же, но ось вращения проходит через один из концов стержня
;
г) тела относительно произвольной оси (теорема Штейнера)
,
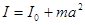где I0 – момент инерции тела относительно оси, параллельной данной и проходящей через его центр инерции;
a – расстояние между параллельными осями.
· Момент силы относительно неподвижной оси вращения
, или M = F× d,
где 
– радиус-вектор;
d – плечо силы F.
· Момент импульса материальной точки относительно неподвижной точки
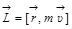, или 
.
· Основное уравнение динамики вращательного движения твердого тела
, или 
.
· Проекция на ось Z момента импульса тела, вращающегося относительно неподвижной оси Z
Lz = Iz w, или 
,
где w - угловая скорость тела.
· Закон сохранения момента импульса (количества движения) для изолированной системы
,
где Ii – момент инерции тел относительно оси Z i;
w i – угловая скорость вращения тел системы вокруг оси Z.
· Кинетическая энергия вращающегося тела относительно неподвижной оси
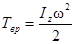, или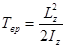 
.
· Работа при вращательном движении
dA = M×dj,
где dj – угол поворота тела.
· Кинематическое уравнение гармонических колебаний материальной точки
,
где х – смещение колеблющейся точки от положения равновесия;
А – амплитуда колебаний;
w – круговая или циклическая частота;
j0 – начальная фаза колебаний;
t – время.
,
где Т – период колебаний точки;
v – частота колебаний.
· Скорость и ускорение материальной точки, совершающей гармонические колебания:
– A wsin(w t + j0);
– A w2cos(w t + j0) = –w2 x.
· Сила, под действием которой точка массой m совершает гармоническое колебание (возвращающая сила)
,
где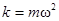 
(m – масса точки), 
.
· Кинетическая и потенциальная энергии колеблющейся точки:
· Полная энергия колеблющейся точки
Е = Т+П =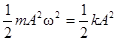 
.
· Период собственных колебаний:
а) математического маятника
,
где l – длина маятника;
g – ускорение свободного падения;
б) пружинного маятника
где m – масса колеблющегося тела;
k – жесткость пружины;
в) физического маятника
,
где I – момент инерции колеблющегося тела относительно оси колебаний;
а – расстояние до центра тяжести маятника от оси колебаний;
– приведенная длина физического маятника.
· Уравнение затухающих колебаний (в среде, где сила сопротивления пропорциональна первой степени скорости)
x = Aoe - d t sin(w t+j1) или x = Aoe - d tcos(w t + j2),
где А – амплитуда в момент времени t = 0;
е – основание натурального логарифма;
d – коэффициент затухания.
· Логарифмический декремент затухания
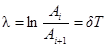
где Аi и Аi+1 – амплитуды двух последовательных колебаний.
· Сложение гармонических колебаний одного направления с одинаковой частотой (периодом), но разными амплитудами и начальными фазами:
, 
Результирующее колебание выражается уравнением
,
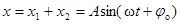где 
– амплитуда результирующего колебания;
– его начальная фаза.
· Сложение двух взаимно перпендикулярных колебаний одинакового периода, но разных амплитуд и начальных фаз.
, 
.
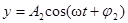Траектория результирующего колебания задается уравнением:
.
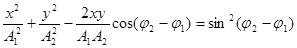В зависимости от разности фаз и амплитуд это будет либо прямая, либо эллипс, либо окружность.
· Длина волны
,
где Т – период колебания;
– скорость распространения волны;
v – частота колебаний.
· Уравнение плоской бегущей волны:
y = A cosw(t – 
) = A cos(w t – kx),
где y – смещение любой из точек среды с координатой x (от источника колебаний) в момент времени t (рисунок 1);
– скорость распространения колебаний в среде;
– волновое число;
l – длина волны.
 | |||||
| |||||
| |||||
 | |||
 | |||
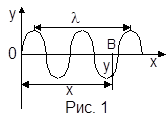· Разность фаз двух колеблющихся точек, находящихся на расстояниях х1 и х2 от источника колебаний
.
· При падении плоской волны на границу раздела двух сред возникает отраженная волна, которая, складываясь с падающей волной, образует стоячую волну.
· Уравнение стоячей волны
y = 2A cos kx sin w t,
где A(x) = 2A cos kx – амплитуда стоячей волны.
· Амплитуда стоячей волны максимальна в точках, удовлетворяющих условию 
и называемых пучностями стоячей волны. Здесь n = 0,1,2,3… (рис. 2; точки А, С, Е,…).
· Амплитуда стоячей волны минимальная в точках, удовлетворяющих условию 
и называемых узлами стоячей волны (рисунок 2; точки В, D, F,…).
Примеры решения задач
Пример 1. Движение тела массой 2 кг задано уравнением х = 6 t 3+3 t +1 (м). Найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело, и импульс тела в конце второй секунды.
| Дано: | Решение: |
| x = 6 t 3+3 t +1 m = 2 кг t = 2 с | Мгновенную скорость находим как производную от координаты по времени:
Мгновенное ускорение определяется первой
|
| (t) -? A(t) -?
F -? p -?
|
производной от скорости по времени или второй производной от координаты по времени:
; a = 36 t.
Сила, действующая на тело, определяется по второму закону Ньютона: F = ma, где a - ускорение в конце второй секунды.
Тогда F = m ×36 t; F = 2×36×2 = 144 (H).
Импульс тела p = m = m (18 t 2+3); p = 2(18×22+3) = 150 (кг×м/с).
Ответ: = 18 t 2+3 (м/с); а = 36 t (м/с2); F = 144 H; p = 150 кг×м/с.
Пример 2. Тело вращается вокруг неподвижной оси по закону j = A+B t +C t 2, где А = 10 рад, В = 20 рад/с, С = –2 рад/с2. Найти полное ускорение точки, находящейся на расстоянии r = 0,1 м от оси вращения, для момента времени t = 4 с.
| Дано: | Решение: |
| А = 10 рад В = 20 рад/с С = – 2рад/с2 r = 0,1 м | Полное ускорение точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения  , направленного по касательной к траектории, и
|
| t = 4 с | нормального ускорения  , направленного к центру кривизны траектории (рисунок 3):
|
| a -? |
.
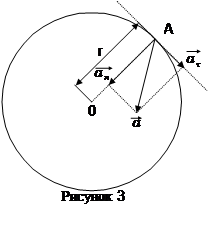
Так как векторы и взаимно перпендикулярны, то модуль ускорения
(1).
Модули тангенциального и нормального ускорения точки вращающегося тела выражаются формулами: 
, 
,
где w – модуль угловой скорости тела;
e – модуль его углового ускорения.
Подставляя выражения 
и 
в формулу (1), находим:
(2).
Угловую скорость w найдем, взяв первую производную угла поворота по времени: 
.
В момент времени t =4 с модуль угловой скорости
w = [20+2×(-2)×4] рад/с = 4 рад/с.
Угловое ускорение найдем, взяв первую производную от угловой скорости по времени: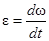 
, e = 2С = 2×(-2) рад/с2 = – 4 рад/с2.
Подставляя значения w, e и r в формулу (2), получаем:
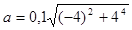м/с2 = 1,65 м/с2.
Ответ: а = 1,65 м/с2.
