| Вар. | Номера задач | ||||||||||
401. Расстояние между двумя когерентными источниками d =0,9 мм. Источники, испускающие монохроматический свет с длиной волны λ =642 нм, расположены на расстоянии l =3,5 м от экрана. Определите число светлых полос, располагающихся на х = 1 см длины экрана.
402. На тонкий стеклянный клин нормально падает монохроматический свет. Наименьшая толщина клина, с которой видны интерференционные полосы, d = 0,1 мкм, расстояние между полосами х = 5 мм. Определите длину волны падающего света и угол между поверхностями клина.
403. На каком расстоянии от экрана находятся когерентные источники света (λ = 0,6 мкм), расстояние между которыми d = 0,4 мм, а ширина светлых интерференционных полос на экране D х = 2 мм? Решение пояснить рисунком.
404. Определите показатель преломления материала, из которого изготовлен клин, преломляющий угол которого α = 3×10-4 рад, если на l = 1 см приходится N = 22 интерференционные полосы максимума интенсивности света. Длина волны нормально падающего монохроматического света λ = 0,415 мкм.
405. На тонкий стеклянный клин (n = 1,6) падает нормально свет с длиной волны λ = 0,5 мкм, расстояние между соседними темными интерференционными полосами в отраженном свете D х = 0,3 мм. Определите угол между поверхностями клина.
406. Расстояние между двумя когерентными источниками света d = 2 мм, они удалены от экрана на l = 2 м. Найти длину волны, излучаемую когерентными источниками, если расстояние на экране между третьим и пятым минимумами интерференционной картины х =1,2 см.
407. На мыльную пленку с показателем преломления n = 1,33 падает по нормали монохроматический свет с длиной волы λ = 0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина dmin пленки?
408. На мыльную пленку (n = 1,33) падает белый свет под углом 45°. При какой наименьшей толщине пленки отраженные лучи будут окрашены в желтый цвет (λ = 600 нм)?
409. Когда на пути одного из интерференционных лучей (λ = 0,8 мкм) в опыте Юнга поместили перпендикулярно ему тонкую стеклянную пластину (n = 1,5), то интерференционная картина на экране изменилась на противоположную. При какой наименьшей толщине dmin пластинки это возможно?
410. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волы λ = 500 нм. Вследствие интерференции отраженный от нее свет был максимально усилен. Определите минимальную толщину dmin пленки, если показатель преломления материала пленки n = 1,4.
411. Установка для получения колец Ньютона освещается монохроматическим светом. Наблюдение ведется в отраженном свете. Радиусы двух соседних темных колец равны соответственно rk = 4,0 мм и rk+1 = 4,38 мм. Радиус кривизны линзы R = 6,4 м. Найти порядковые номера колец и длину волны падающего света.
412. Установка для наблюдения колец Ньютона в отраженном свете освещается монохроматическим светом, падающим нормально. После того как пространство между линзой и стеклянной пластинкой заполнили жидкостью, радиусы темных колец уменьшились в 1,25 раза. Найти показатель преломления жидкости.
413. Плосковыпуклая линза с радиусом сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметр десятого темного кольца Ньютона в отраженном света Dk = 1 мм. Определите длину волны света.
414. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (λ = 590 нм). Радиус кривизны линзы R = 5 см. Определите толщину dk воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо.
415. Плосковыпуклая стеклянная линза с фокусным расстоянием F = 1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца в проходящем свете r5 = 1,1 мм. Определите длину световой волны λ.
416. Установка для получения колец Ньютона освещается светом от ртутной лампы, падающим нормально. Наблюдение производится в проходящем свете. Какое по порядку светлое кольцо, соответствующее линии λ 1 = 579,1 нм, совпадает со следующим светлым кольцом, соответствующим линии λ 2 = 577 нм?
417. Плосковыпуклая линза с показателем преломления n = 1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца Ньютона в отраженном свете (λ = 0,6 мкм) равен 0,9 мм. Определите фокусное расстояние линзы.
418. Установка для наблюдения колец Ньютона в отраженном свете освещается монохроматическим светом λ = 600 нм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено водой. Найти толщину слоя воды между линзой и стеклянной пластинкой в том месте, где наблюдается второе светлое кольцо.
419. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,65 мкм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение ведется в проходящем свете. Радиус кривизны линзы R = 4 м. Определите показатель преломления жидкости, если радиус третьего светлого кольца r = 2,3 мм.
420. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны R = 0,5 м находится жидкость. Найдите показатель преломления жидкости, если радиус третьего светлого кольца Ньютона в проходящем свете с длиной волны λ = 0,6 мкм равен r 3 = 0,82 мм.
421. На пластинку с щелью шириной а = 0,1 мм падает нормально к ней монохроматический свет с длиной волны λ = 0,7 мкм. Определите ширину центральной светлой полосы, если экран удален от щели на расстояние l = 1 м.
422. На дифракционную решетку длиной l = 15 мм, содержащую N =3000 штрихов, падает нормально монохроматический свет с длиной волны λ = 550 нм. Определите: 1) общее число дифракционных максимумов, наблюдаемых в решетке; 2) угол, соответствующий последнему максимуму.
423. Монохроматический свет нормально падает на дифракционную решетку. Определите угол дифракции, соответствующий максимуму пятого порядка, если максимум третьего порядка отклонен на j 1 = 20°.
424. На дифракционную решетку нормально падает монохроматический свет. Определите угол дифракции для линии λ = 0,55 мкм в четвертом порядке, если этот угол для линии λ = 0,6 мкм в третьем порядке составляет 30°.
425. На узкую щель нормально падает монохроматический свет. Угол дифракционного максимума для спектра второго порядка j = 2°. Определите, сколько длин волн падающего света укладывается на ширине щели.
426. Две дифракционные решетки имеют одинаковую ширину l = 4 мм, но разные периоды, равные d 1 = 4 мкм и d 2 = 2 мкм. Определите и сравните их наибольшую разрешающую способность для желтой линии натрия (λ = 0,589 нм).
427. Какую разность длин волн может «разрешить» дифракционная решетка в спектре второго порядка для фиолетовых лучей (λ = 0,4 мкм), если период решетки d = 2 мкм, а ширина ее l = 2 см?
428. На грань кристалла каменной соли падает пучок параллельных рентгеновских лучей с длиной волны λ = 0,15 нм. Под каким углом к атомной плоскости наблюдается дифракционный максимум третьего порядка, если расстояние между атомными плоскостями кристалла d =0,285 нм.
429. На дифракционную решетку с постоянной d = 5 мкм под углом α = 30° падает монохроматический свет с длиной волны λ =0,5 мкм. Определите угол j дифракции для главного максимума третьего порядка
430. Определите длину λ 1 световой волны спектральной линии, изображение которой, даваемое дифракционной решеткой в спектре третьего порядка, совпадает с изображением линии λ 2 = 0,38 мкм в спектре четвертого порядка.
431. Луч света переходит из воды (n 1 = 1,33) в алмаз (n 2 = 2,42) так, что луч, отраженный от границы раздела этих сред, оказывается максимально поляризован. Определите угол γ между падающим и преломленным лучами.
432. Угол между плоскостями поляризации николей равен j = 30°. Интенсивность света, прошедшего такую систему, уменьшилась в n = 5 раз. Пренебрегая потерей света при отражении, определите коэффициент поглощения света k в каждом из николей, считая их одинаковыми.
433. Луч света переходит из кварца (n 1 = 1,55) в жидкость, частично отражаясь, частично преломляясь. Отраженный луч максимально поляризован при угле падения 
. Определите показатель преломления n 2 жидкости и скорость распространения света в ней.
434. При прохождении естественного света через два николя, угол между плоскостями поляризации которых j = 45°, происходит ослабление света. Коэффициент поглощения света в поляризаторе равен k 1= 0,08, а в анализаторе k 2= 0,1. Найдите, во сколько раз изменилась интенсивность естественного света после прохождения этой системы.
435. Плоскополяризованный свет, длина которого в вакууме λ = 590 нм, падает на пластинку исландского шпата перпендикулярно его оптической оси. Принимая показатели преломления исландского шпата для обыкновенного и необыкновенного лучей соответственно n 0=1,66 и nе =1,49, определите длины волн этих лучей в кристалле.
436. Предельный угол полного внутреннего отражения для пучка света на границе жидкости с воздухом равен 43°. Каков должен быть угол падения света из воздуха на поверхность жидкости, чтобы отраженный луч был максимально поляризован?
437. Угол максимальной поляризации при отражении света от кристалла каменной соли равен 57°. Определите скорость распространения света в этом кристалле.
438. Под каким углом к горизонту должно находиться Солнце, чтобы лучи, отраженные от поверхности озера, были максимально поляризованы?
439. Луч света, проходящий через слой воды (n 1=1,33), падает на кварцевую пластинку (n 2=1,55), частично отражается, частично преломляется. Преломленный луч перпендикулярен отраженному. Определите угол между падающим и преломленным лучами.
440. На пластинку из кварца перпендикулярно ее оптической оси падает плоскополяризованный свет, длина волны которого в вакууме λ =530 нм. Определите показатели преломления кварца для обыкновенного (n 0 ) и необыкновенного (nе) лучей, если длины волн этих лучей в кристалле соответственно равны λ 0=344 нм и λе =341 нм.
441. Определите максимальную скорость 
фотоэлектрона, вырванного с поверхности платины (работа выхода электрона А = 6,3 эВ), при облучении γ-квантом с энергией ε = 1,53 МэВ.
442. Определите длину волны γ-излучения, падающего на платиновую пластину (работа выхода электрона из платины А = 6,3 эВ), если максимальная скорость фотоэлектронов была = 3 Мм/с.
443. Определите максимальную скорость фотоэлектронов, вырываемых с поверхности меди (работа выхода электрона А = 5,2 эВ), при облучении γ-излучением с длиной волны λ = 2,5 пм.
444. Определите, на какое максимальное расстояние от поверхности электрода может удалится фотоэлектрон, вырванный с поверхности серебряного электрода при облучении его монохроматическим светом с длиной волны λ = 85 нм, если вне электрода имеется задерживающее электрическое поле напряженностью Е = 10 В/см. Красная граница фотоэффекта для серебра λ 0 = 264 нм.
445. Фотоэлектроны вырываются с поверхности серебряной пластинки (работа выхода А = 4,7 эВ) фотонами с энергией ε= 5 эВ. Определите максимальный импульс, передаваемый поверхности этой пластинки при вылете электрона и полный импульс, полученный пластинкой.
446. Если освещать катод вакуумного фотоэлемента монохроматическим светом с длиной волны λ 1 = 350 нм, то фототок прекращается при задерживающем напряжении U 1 = 12,5 В. Как изменится задерживающее напряжение при увеличении длины волны на 20%?
447. На поверхность металла падает пучок ультрафиолетового излучения (λ = 0,25 мкм). Красная граница фотоэффекта λ 0 = 0,62 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии?
448. При освещении катода вакуумного фотоэлемента монохроматическим светом частотой v 1=2×1015 Гц фотоэлектроны полностью задерживаются тормозящим полем при напряжении U 1 = 7 В. При увеличении частоты падающего света на 45% задерживающее напряжение оказалось равным U 2 = 10,7 В. Вычислите по этим экспериментальным данным постоянную Планка.
449. Энергия фотона равна кинетической энергии электрона, имевшего начальную скорость 
=106 м/с и ускоренного разностью потенциалов U = 4 В. Определите длину волны фотона.
450. Уединенный цинковый шарик облучают монохроматическим светом длиной волны λ = 40 нм. Определите, до какого потенциала зарядится шарик. Работа выхода электронов из цинка А = 4,0 эВ.
451. Во сколько раз увеличится поток излучения абсолютно черного тела, если максимум энергии излучения передвинется от красной границы (λк = 0,76 мкм) видимого спектра к его фиолетовой границе (λф = 0,38 мкм)?
452. Какую мощность нужно подводить к свинцовому шарику радиусом r = 4 см, чтобы поддерживать его температуру t 1 = 27°С, если температура окружающей среды t 2 = –23°С? Считать, что теплота теряется только вследствие излучения. Поглощательная способность свинца α т=0,6.
453. Определите количество теплоты, теряемое поверхностью расплавленной платины при t °= 1770°С за t = 1 мин., если площадь поверхности S = 100 см2. Коэффициент поглощения принять равным α т = 0,8.
454. Максимум энергии излучения абсолютно черного тела приходится на длину волны λ = 450 нм. Определите температуру и энергетическую светимость тела.
455. Площадь поверхности нити накала 60-ваттной вольфрамовой лампы накаливания S =0,5 см2. Коэффициент поглощения вольфрама α т=0,6. Определите температуру нити накала.
456. Принимая спектр Солнца за спектр излучения абсолютно черного тела, определите мощность суммарного (интегрального) (т.е. приходящегося на все длины волн) излучения, если максимум испускательной способности соответствует длине волны λmax = 0,48 мкм. Радиус Солнца считать равным Rс = 6,95×105 км.
457. Определите длину волны, соответствующую максимальной спектральной плотности энергетической светимости абсолютно черного тела равной (rλ, т) max = 4,16×1011 Вт/м3. Постоянные Вина b = 2,9×10-3 м×К; С = 1,3×105 Вт/м3×K5.
458. Максимум спектральной плотности энергетической светимости (rλ, т) яркой красноватой звезды Арктур приходится на длину волны λ =5800 Å. Принимая, что звезда излучает как абсолютно черное тело, определите температуру поверхности звезды. (Необходимые постоянные см. задачу № 457).
459. Муфельная печь, потребляющая мощность Р = 1 кВт, имеет отверстие площадью S = 100 cм2. Определите долю η мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна Т = 1 кK.
460. Средняя энергетическая светимость поверхности Земли равна Re = 0,54 Дж/см2×мин. Если условно считать, что Земля излучает как серое тело с коэффициентом черноты α т = 0,25, определите длину волы λmax, на которую приходится максимум энергии излучения.
461. Определите силу светового давления на зеркальную поверхность площадью S = 100 см2, если интенсивность светового потока, падающего нормально на эту поверхность, равна Ее = 2,5 кВт/м2.
462. Определите давление на черную поверхность, создаваемое светом с длиной волны λ = 0,4 мкм, если ежесекундно на поверхность S = 1 см2 падает n = 6×1016 фотонов.
463. Световое давление, испытываемое зеркальной поверхностью площадью S = 1 см2, равно р = 10-6 Па. Определите длину волны монохроматического света, если ежесекундно падает n = 5×1012 фотонов.
464. Определите давление света на стенки колбы электрической лампы мощностью Р = 100 Вт. Колба лампы – сфера радиусом R = 5 см, стенки которой отражают 10% падающего на них света. Считать, что вся потребляемая лампой мощность идет на излучение.
465. Давление монохроматического света с длиной волны λ = 0,6 мкм на черную поверхность равно р = 10-7 Па. Сколько фотонов падает ежесекундно на 1 м2 поверхности?
466. Ежесекундно на зеркальную поверхность площадью S = 1 м2 нормально падает n = 15×1020 фотонов. Определите длину волны монохроматического света, если давление света на поверхность р = 5 мкПа.
467. На зеркальную поверхность нормально падает монохроматический свет с длиной волны λ = 0,55 мкм. Поток излучения Фе составляет 0,45 Вт. Определите: 1) число фотонов, падающих на поверхность за время t = 5 с; 2) силу давления, испытываемую этой поверхностью.
468. Точечный источник монохроматического (λ = 1 нм) излучения находится в центре сферической зачерненной колбы радиусом R = 10 см. Определите световое давление р, производимое на внутреннюю поверхность колбы, если мощность источника Р = 1 кВт.
469. Параллельный пучок монохроматических лучей (λ = 0,5 мкм) падает на зачерненную поверхность и производит на нее давление р =10-9 Н/см2. Определите концентрацию n 0 фотонов в световом пучке.
470. Давление света, производимое на зеркальную поверхность р = 5 мПа. Определите концентрацию n 0 фотонов вблизи поверхности, если частота света, падающего на поверхность, v = 6×1014 Гц.
471. В результате комптоновского эффекта электрон приобрел кинетическую энергию (отдачи) Тmax = 0,5 МэВ. Определите энергию ε 1 падающего фотона, если длина волны рассеянного фотона λ 2 = 0,025 нм.
472. Фотон с энергией ε1 = 1,3 МэВ в результате эффекта Комптона был рассеян на свободном электроне. Определите комптоновскую длину волны λ 2 рассеянного фотона, если угол рассеяния фотона θ = 60°.
473. Фотон с импульсом р 1 = 1,02 МэВ/с (здесь с – скорость света в вакууме) в результате эффекта Комптона был рассеян на свободном электроне на угол θ = 30°. Определите импульс р 2 (в МэВ/с) рассеянного фотона.
474. Фотон с длиной волны l = 1 пм при соударении со свободным электроном испытал комптоновское рассеяние под углом θ = 60°. Определите долю энергии, оставшуюся у фотона.
475. Фотон с энергией ε1 = 0,51 МэВ в результате эффекта Комптона был рассеян на угол θ = 180°. Определите энергию электрона отдачи.
476. Фотон с длиной волны λ = 6 пм испытал комптоновское рассеяние под углом θ = 90° на первоначально покоившемся свободном электроне. Определите импульс электрона отдачи.
477. Фотон с энергией ε1=0,5 МэВ рассеялся под углом θ = 180° на свободном электроне. Определите долю энергии фотона, приходящуюся на рассеянный фотон.
478. Фотон с энергией ε1=0,3 МэВ рассеялся под углом θ = 120° на первоначально покоившемся электроне. Определите кинетическую энергию Те электрона отдачи.
479. В результате эффекта Комптона фотон с энергией ε1=1,5 МэВ был рассеян на свободном электроне на угол θ = 120° Определите энергию ε2рассеянного фотона.
480. Определите длину волны рентгеновского излучения, если при комптоновском рассеянии этого излучения под углом θ = 60° на свободном электроне длина волны рассеянного излучения оказалась равной λ 2 = 57 пм.
6. ЭЛЕМЕНТЫ АТОМНОЙ ФИЗИКИ
И КВАНТОВОЙ МЕХАНИКИ.
ФИЗИКА АТОМНОГО ЯДРА
Основные законы и формулы
· Первый постулат Бора. Электрон в атоме водорода движется, не излучая, по круговой орбите, для которой момент импульса электрона
, или 
,
где me – масса электрона;
– скорость электрона на n -ой орбите;
rn – радиус n -ой стационарной орбиты;
ħ = 1,05×10-34 Дж×с, или h = 6,63×10-34 Дж×с – постоянная Планка;
n = 1, 2, 3,… – квантовое число (номер орбиты электрона).
· Второй постулат Бора. При переходе электрона с одной орбиты на другую атом водорода излучает или поглощает квант энергии:
,
где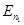 
и 
– полные энергии электрона в атоме на соответствующей орбите.
· Полная энергия электрона в атоме водорода
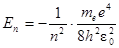(n = 1, 2, 3,…),
где n – номер орбиты;
me – масса электрона;
е – заряд электрона;
ε0 = 8,85×10-12 Ф/м – электрическая постоянная;
h – постоянная Планка.
· Формула, позволяющая найти частоты v или длины волн λ, соответствующие линиям водородного спектра (сериальная формула Бальмера)
,
где R – постоянная Ридберга (R = 1,10×107 м-1);
с – скорость света в вакууме;
n1 и n2 – квантовые числа, определяющие номера орбит электрона.
Для водородоподобных ионов формула имеет вид:
,
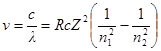где Z – порядковый номер в таблице Менделеева.
· Длина волны де Бройля
,
где p=m 
– модуль импульса движущейся частицы.
· Импульс частицы и его связь с кинетической энергией T:
а) 
; 
;
б) 
; 
,
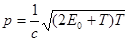где m 0 – масса покоя частицы;
m – релятивистская масса частицы;
– скорость частицы;
с – скорость света в вакууме;
Е 0 – энергия покоя частицы (Е 0 = m 0 с2).
· Соотношение неопределенностей:
а) для координаты и импульса
,
где D Рх – неопределенность проекции импульса на ось Х;
D х – неопределенность координаты;
б) для энергии и времени
,
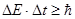где D Е – неопределенность энергии;
D t – неопределенность времени жизни квантовой системы в данном энергетическом состоянии.
· Одномерное уравнение Шредингера для стационарных состояний
,
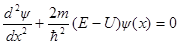где ψ(х) – волновая функция, описывающая состояние частицы;
m – масса частицы;
Е – полная энергия частицы;
U = U(х) – потенциальная энергия частицы.
· Плотность вероятности
,
где d ω(x) – вероятность того, что частица может быть обнаружена вблизи точки с координатой x на участке dx.
· Вероятность обнаружения частицы в интервале от х 1 до х 2
· Решение уравнение Шредингера для одномерного бесконечно глубокого, прямоугольного потенциального ящика:
а) 
– собственная нормированная волновая функция;
б)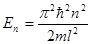 
– собственное значение энергии, где n – квантовое число (n = 1, 2, 3,…); l – ширина ящика.
В области 0 £ x £ l U = ∞ и ψ (х) = 0.
· Коэффициент прозрачности прямоугольного потенциального барьера, т.е. вероятность прохождения (туннелирования) микрочастицы сквозь барьер:
,
где D 0 – коэффициент, по порядку величины близкий к единице;
U – высота потенциального барьера;
l – его ширина;
Е – энергия частицы;
m – масса частицы.
· Закон радиоактивного распада
dN = – λ × N × dt, или 
,
где dN – число ядер, распадающихся за интервал времени dt;
N – число ядер, не распавшихся к моменту времени t;
N 0 – число ядер в начальный момент (t = 0);
λ – постоянная радиоактивного распада.
· Число ядер, распавшихся за время t:
.
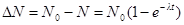· Период полураспада
.
· Среднее время жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшилось в е раз:
.
· Число атомов, содержащихся в радиоактивном изотопе
,
где m – масса изотопа;
М – молярная масса;
NA – постоянная Авогадро (NA =6,02×1023 моль-1).
· Активность радиоактивного изотопа
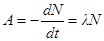, или 
,
где dN – число ядер, распадающихся за интервал времени dt;
А 0 – активность изотопа в начальный момент времени (t = 0), А 0 =λN 0.
· Удельная активность изотопа
.
· Дефект массы ядра
,
где Z – зарядовое число (число протонов в ядре);
А – массовое число (число нуклонов в ядре);
(А-Ζ) – число нейтронов в ядре;
mр – масса протона;
mn – масса нейтрона;
mя – масса ядра.
· Энергия связи ядра
Есв = D mс2,
где Δ m – дефект массы ядра;
с – скорость света в вакууме.
Во внесистемных единицах энергия связи ядра равна Есв = 931×Δ m Мэв, где дефект массы Δ m – в а.е.м.; 931 – коэффициент пропорциональности (1 а.е.м. ~ 931 МэВ).
· Правило смещения:
1) для α -распада: 
;
2) для β- -распада: 
;
3) для β+ -распада: 
.
· Ядерные реакции. Символическая запись ядерной реакции может быть дана или в развернутом виде, например:
или сокращенно
.
При сокращенной записи порядковый номер атома не пишут, так как он определяется химическим символом атома. В скобках на первом месте ставят обозначение бомбардирующей частицы, на втором – обозначение частицы, вылетающей из составного ядра, и за скобками – химический символ ядра-продукта.
Обозначения частиц: р – протон, n – нейрон, d – дейтрон, t – тритий (тритон), α -альфа-частица, γ-гамма-фотон.
· Энергетический эффект ядерной реакции
Q = c 2[(m 1 +m 2) –(m 3 +m 4)],
где m 1 – масса покоя ядра-мишени;
m 2 – масса покоя бомбардирующей частицы,
(m 3 + m 4) – сумма масс покоя ядер продуктов реакции.
Если m 1 + m 2 > m 3 + m 4, то энергия освобождается, реакция экзотермическая. Если m 1 + m 2 < m 3 + m 4, то энергия поглощается, реакция эндотермическая.
· При решении задач на ядерные реакции применяются законы сохранения:
1) электрического заряда: z 1 + z 2 = z 3 + z 4;
2) суммарного числа нуклонов: А 1 + А 2 = А 3 + А 4;
3) релятивистской полной энергии: Е 1 + Е 2 = Е 3 + Е 4; или
,
где 
– сумма энергий покоя частиц и их кинетических энергий до реакции; справа то же для частиц после реакции;
4) импульса: р 1 + р 2 = р 3 + р 4.
Примеры решения задач
Пример 1. Определите потенциал ионизации и первый потенциал возбуждения атома водорода.
Решение.
Потенциалом ионизации Ui называют ту наименьшую разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с данным невозбужденным атомом ионизировать его. Работа по удалению электрона из атома Аi равна работе сил электрического поля, ускоряющего электрон, eUi, поэтому Аi=eUi.
Учитывая квантовый характер поглощения энергии атомом, можно сказать, что работа ионизации Аi равна кванту энергии hv, поглощенному атомом водорода при переходе электрона с первой боровской орбиты на бесконечно удаленную орбиту. Тогда, применив сериальную формулу Бальмера и положив в ней n 1 = 1; n 2 = ∞, получим:
.
Следовательно
;
.
Первый потенциал возбуждения U1 есть та наименьшая разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с невозбужденным атомом перевести его в первое возбужденное состояние. Для атома водорода это соответствует переходу электрона с первой боровской орбиты на вторую. Приравняв работу сил ускоряющего электрического поля eU1 кванту энергии hν, поглощенному атомом при его переходе в первое возбужденное состояние, получим:
,
где n 1=1, n 2=2. Откуда:
.
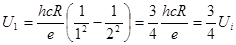Производим вычисления:
.
Ответ: Ui = 13,6 В; U 1 = 10,2 В.
Пример 2. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Определите длину волны де Бройля электрона для двух случаев: 1) U 1 = 51 В; 2) U 2 = 510 кВ.
| Дано: | Решение: |
| m 0 = 9,1×10-31 кг e = 1,6×10-19 Кл U 1 = 51 B U 2 = 510 кВ = 51×104 В | Длина волны де Бройля для частицы определяется формулой
 , (1)
где р – импульс частицы.
|
| λ 1-? λ 2-? |
Импульс частицы связан с ее кинетической энергией Т соотношением:
1) в нерелятивистском (классическом) случае (когда кинетическая энергия частицы Т много меньше ее энергии покоя Е 0 = m 0 с2):
, (2)
где m 0 – масса покоя частицы;
2) в релятивистском случае (когда кинетическая энергия Т сравнима с энергией покоя Е 0 частицы):
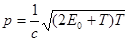, (3)
где с – скорость света в вакууме.
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U 1 = 51 В и U 2 =510 кВ, с энергией покоя электрона Е 0 = m 0 с 2 = 0,51 МэВ и в зависимости от этого решим, какую из формул (2) или (3) следует применить для вычисления длины волны де Бройля.
Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U 1 равна T = еU.
В первом случае
T 1= еU 1 = 1,6×10-19 Кл × 51 В = 81,6×10-19 Дж =
= 51 эВ = 0,51×10-4 МэВ,
что много меньше энергии покоя электрона Е 0 = 0,51 МэВ. Следовательно, в этом случае можно применять формулу (2). Тогда:
.
Во втором случае кинетическая энергия
T 2 = еU 2 = 51×104 эВ = 0,51 МэВ,
т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (3). Тогда получим:
;
Так как Т 2 = Е 0 = m 0 c2, то получим:
;
Произведем вычисления:
.
Ответ: λ 1 = 172 пм; λ 2 = 1,4 пм.
Пример 3. Используя соотношение неопределенностей Гейзенберга, показать, что ядра атомов не могут содержать электронов. Считать радиус ядра равным Rя = 10-13 см.
| Дано: | Решение: |
| Rя = 10-13 см = 10-15 м ħ = 1,05×10-34 Дж×с | Соотношение неопределенностей для координаты и импульса имеет вид |
Δ х· Δ рх ≥ ћ,
где Δ х – неопределенность координаты частицы (в данном случае электрона);
Δ рх – неопределенность импульса электрона;
ћ – постоянная Планка.
Если неопределенность координаты принять равной радиусу ядра, т.е. Δ х = Rя, то неопределенность импульса электрона выразим следующим образом:
.
Так как Δ рх=mΔVх, то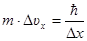 
и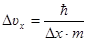 
.
Вычислим неопределенность скорости электрона:
.
Сравнивая полученное значение 
со скоростью света в вакууме с = 3×108 м/с, видим, что 
, а это невозможно. Следовательно, ядра не могут содержать электронов.
Пример 4. Электрон находится в бесконечно глубоком, прямоугольном, потенциальном ящике шириной l. В каких точках в интервале (0< х < l) плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить значение плотности вероятности для этих точек. Решение пояснить графиком.
| Дано: | Решение: |
0< х < l
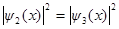
| Вероятность обнаружить частицу в интервале х 1< х < х 2 определяется выражением:
 ,
|
х -?  -?
|
где ψn(х) – нормированная собственная ψ -функция, отвечающая данному состоянию. Нормированная собственная ψ -функция, описывающая состояние электрона в потенциальном ящике, имеет вид:
.
Возбужденным состоянием (n 1=2) и (n 2=3) отвечают собственные функции:
и 
.
По условию задачи 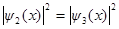, тогда получим:
, или
.
.
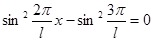Используя соотношения:
,
,
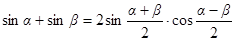получим:
;
. (*)
Так как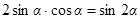 
, то выражение (*) примет вид:
.
Решим полученное уравнение:
1) 
, или 
, откуда 
, а 
, где n =0, 1, 2, 3,…
Тогда 
; 
; 
; 
.
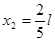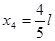2) 
, или 
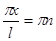, откуда 
, а 
– это значение не удовлетворяет условию задачи (0< х < l).
Следовательно, ; ; ; .
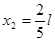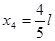Вычислим значение плотности вероятности в этих точках:
.
Так как 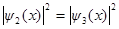, то вычисление сделаем только для состояния n =2 (электрон находится на втором энергетическом уровне):
Для :
;
: 
;
: 
;
: 
.
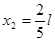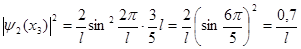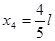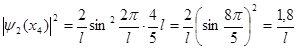Итак, для точек х 1 и х 4: 
;
Для точек х 2 и х 3: 
.
Построим график (рисунок 54).
Пример 5. Определите начальную активность А 0 радиоактивного препарата магния 27 Mg массой m = 0,2 мкг, а также его активность А через время t = 6 ч. Период полураспада Т1/2 магния считать известным.
| Дано: | Решение: |
| 27 Mg m = 0,2 мкг = 2×10-10 кг М = 27×10-3 кг/моль t = 6 ч = 6×3,6×103 с Т 1/2 = 10 мин = 600 с | Активность А изотопа характеризует скорость радиоактивного распада и определяется отношением числа dN ядер, распавшихся за интервал времени dt, к этому интервалу: |
| А 0-? А -? |
.
Знак «минус» показывает, что число N радиоактивных ядер с течением времени убывает.
Воспользуемся законом радиоактивного распада
N = N 0 е-λt.
Тогда: 
.
Начальную активность А 0 препарата получим при t = 0: А 0 = λN 0, где постоянная радиоактивного распада 
. Число N 0 радиоактивных ядер, содержащихся в изотопе массой m, равно: 
, где М – молярная масса изотопа. NА = 6,02×1023 моль-1 – постоянная Авогадро.
Следовательно, 
;
, или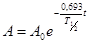 
.
Произведем вычисления:
.
.
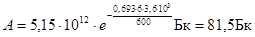Ответ: А 0 = 5,15 ТБк; А = 81,5 Бк.
Пример 6. Вычислите дефект массы и энергию связи ядра 
.
Решение.
Дефект массы ядра Δ m есть разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, то есть:
, (1)
где Z – атомный номер изотопа (число протонов в ядре);
А – массовое число (число нуклонов, составляющих ядро);
|
В справочных таблицах всегда даются массы нейтральных атомов, но не ядер, поэтому формулу (1) целесообразно преобразовать так, чтобы в нее входила масса mа нейтрального атома. Масса нейтрального атома равна сумме масс ядра и электронов, составляющих электронную оболочку атома: mа = mя + Zmе, откуда mя = mа – Zmе. Тогда формула (1) примет вид:
.
Замечая, что mp + me = 
(масса атома водорода), окончательно получим:
.
Подставив в это выражение числовые значения масс в а.е.м. (см. табл. 15 и 17 Приложения), получим:
а.е.м
Для вычисления энергии связи ядра воспользуемся формулой
Есв = 931Δ m (МэВ ):
Есв = 931×0,04216 МэВ = 39,2 МэВ.
Ответ:Δ m = 0,04216 а.е.м.; Есв = 39,2 МэВ.
Пример 7. При соударении α -частицы с ядром бора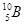 
произошла ядерная реакция, в результате которой образовалось два новых ядра. Одним из этих ядер было ядро атома водорода 
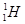. Определите порядковый номер и массовое число второго ядра, запишите символически ядерную реакцию и определите ее энергетический эффект.
Решение.
Обозначим неизвестное ядро символом 
. Так как α -частица представляет собой ядро гелия 
, запись реакции имеет вид:
.
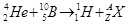Применив закон сохранения заряда, получим уравнение: 2+5=1+ Z, откуда Z =6. Применив закон сохранения числа нуклонов, получим уравнение: 4+10=1+ А, откуда А =13. Следовательно, неизвестное ядро является ядром атома изотопа углерода 
. Теперь можем записать ядерную реакцию в окончательном виде:
.
Энергетический эффект Q ядерной реакции определяется по формуле:
Q = 931[(mHe + mB) – (mH + mC)] МэВ.
Заменяя массы исходных ядер и массы ядер продуктов реакции массами нейтральных атомов (см. табл.15 Приложения) и подставив их в расчетную формулу, получим:
Q = 931[4,00260+10,01294) – (1,00783+13,00335)] МэВ = 4,06 МэВ.
Ответ: Q = 4,06 МэВ.
Пример 8. Определить энергию реакции 10 В (n,α)7 Li, протекающей в результате взаимодействия весьма медленных нейтронов с покоящимися ядрами бора. Найти также кинетические энергии продуктов реакции.
Решение.
Ядерная реакция 10 В (n,α)7 Li состоит в следующем. Ядро бора 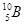, поглотив медленный нейтрон 
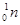, превращается в промежуточное ядро 
. Последнее, будучи возбужденным, испускает α -частицу (т.е. ядро гелия ), превращаясь в ядро лития . В развернутом виде реакция записывается так:
.
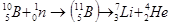Энергия ядерной реакции (или тепловой эффект реакции) Q определяется по формуле:
Q 
Дж, (1)
или Q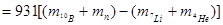 
МэВ.
Заменив массы покоя ядер атомов массами покоя самих атомов (см. табл. 15 Приложения), получим:
Q = 931(10,01294+1,00867–7,01601–
– 4,00260) МэВ = 2,8 МэВ.
Чтобы найти кинетические энергии продуктов реакции – ядра лития 7 Li и α -частицы, применим закон сохранения релятивистской энергии и закон сохранения импульса:
, или
;
с учетом равенства (1) получим:
Q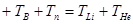 
.
Из условия задачи следует, что величинами TB и Tn можно пренебречь. Тогда получим для суммы кинетических энергий частиц 7 Li и 4 Не:
TLi + THе = Q (2)
По закону сохранения импульса: 
.
Полагая суммарный импульс частиц до реакции равным нулю, получим:
.
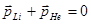Отсюда для модулей импульсов имеем: 
.
Импульсы частиц и их кинетические энергии связаны соотношением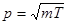 
. Следовательно:
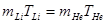(3)
Решаем систему уравнений (2), (3):
Т.к. 
Q 
, то 
(Q ),
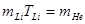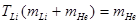Q Þ 
;
.
Произведем вычисления:
.
.
Ответ: Q = 2,8 МэВ; ТLi = 1,02 МэВ; ТНе = 1,78 МэВ.
Пример 9. Позитрон с кинетической энергией Т = 0,75 МэВ налетает на покоящийся свободный электрон. В результате аннигиляции возникает два γ-фотона с одинаковыми энергиями. Определите угол θ между направлениями из разлета.
| Дано: | Решение: |
| Т = 0,75 МэВ = 0,75×1,6×10-13 Дж m 0 = 9,1×10-31 кг e1 = e2 = e | Процесс аннигиляции электрона е- и позитрона е+ происходит по схеме е-+е+→γ+γ и подчиняется |
| θ -? |
законам сохранения энергии и импульса. Согласно закону сохранения импульса, импульс позитрона 
равен векторной сумме импульсов γ-фотонов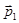 
и 
(рисунок 55): 
.
При этом 
, где ε– энергия каждого γ-фотона.
Из рисунка 55 получим: 
, тогда:
(*)
Чтобы вычислить угол θ, надо определить импульс позитрона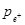 
и энергию ε каждого γ-фотона. Импульс позитрона найдем, зная его кинетическую энергию Т. Поскольку величина Т превышает энергию покоя позитрона m 0 c 2 = 0,511 МэВ, то позитрон следует рассматривать как релятивистскую частицу. В этом случае импульс частицы выражается формулой 
.
Энергию γ-фотона ε определим с помощью закона сохранения релятивистской энергии:
