Сведения о приближенных вычислениях 3 страница

Тогда период колебаний стержня

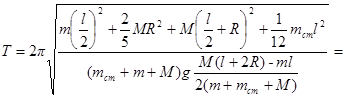
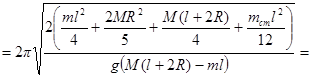
Произведем вычисления:

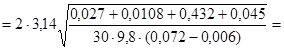
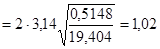с.

Ответ: Т = 1,02 с.

2. МОЛЕКУЛЯРНАЯ ФИЗИКА

ТЕРМОДИНАМИКА

Основные законы и формулы

· Количество вещества[1] тела (системы)

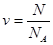где N – число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему);

N_A – постоянная Авогадро (N_A = 6.02×10²³ моль^-1).

· Молярная масса вещества

где m – масса однородного тела (системы);

n – количество вещества этого тела.

· Относительная молекулярная масса вещества

где n_i – число атомов i -го химического элемента, входящих в состав молекулы данного вещества;

A_ri – относительная атомная масса этого вещества.

Относительные атомные массы приводятся в таблице Д. И. Менделеева.

· Связь молярной массы М с относительной молекулярной массой вещества

M=M_r ×10^-3 кг/моль.

· Количество вещества смеси газов

где n_i, m_i, M_i – соответственно количество вещества, масса, молярная масса i -го компонента смеси.

· Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

где m – масса газа;

M – молярная масса газа;

R – молярная газовая постоянная;

n – количество вещества;

T – термодинамическая температура.

· Основные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: T =const, m =const) PV =const,

или для двух состояний газа P₁V₁=P₂V₂;

б) закон Гей-Люссака (изобарный процесс: P =const; m =const)

=const,

или для двух состояний ;

в) закон Шарля (изохорный процессе: V =const, m =const)

=const,

или для двух состояний ;

г) объединенный газовый закон (m=const)

=const, или ,

где P₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии;

P₂, V₂, T₂ – те же величины в конечном состоянии.

· Закон Дальтона, определяющий давление смеси газов:

P=P₁+P₂+…+P_n,

где P_i – парциальные давления компонентов смеси;

n – число компонентов смеси.

Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

· Концентрация молекул

где N – число молекул, содержащихся в данной системе;

r – плотность вещества;

V – объем системы.

Формула справедлива не только для газов, но и для агрегатного состояния вещества.

· Зависимость давления газа от концентрации n молекул и температуры:

p=nkT,

где k – постоянная Больцмана ().

· Основное уравнение молекулярно-кинетической теории идеальных газов

или ,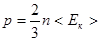

где n – концентрация молекул;

m_o – масса одной молекулы;

< _кв > – средняя квадратичная скорость молекул;

< E_к > – средняя кинетическая энергия поступательного движения молекулы газа.

· Средняя полная кинетическая энергия молекулы газа

где i - число степеней свободы молекулы. (i = i_пост+i_вращ)

· Скорости молекул:

а) - средняя арифметическая;

б) - средняя квадратичная;

в) - наиболее вероятная,

где m_o – масса одной молекулы.

· Относительная скорость молекулы

где – скорость данной молекулы.

· Среднее число соударений, испытываемых молекулой газа за 1 секунду:

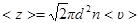где d – эффективный диаметр молекулы;

n – концентрация молекул;

< > – средняя арифметическая скорость молекул.

· Средняя длина свободного пробега молекул газа

· Закон Ньютона для внутреннего трения (вязкости)

где F – сила внутреннего трения между движущимися слоями газа (жидкости) площадью S;

– градиент скорости;

h – коэффициент внутреннего трения (динамическая вязкость).

· Молярные теплоемкости газа при постоянном объеме (C_V) и постоянном давлении (C_P):

, .

· Связь между удельной c и молярной C_n теплоемкостями

, .

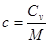· Уравнение Майера для молярных теплоемкостей газа

C_P– C_V = R.

· Внутренняя энергия идеального газа

где C_V – теплоемкость одного моля газа при постоянном объеме.

· Первое начало термодинамики

Q = D U + A,

где Q – количество теплоты, сообщенное системе (газу) или отданное ею;

D U – изменение внутренней энергии системы;

A – работа, совершенная системой против внешних сил.

· Изменение внутренней энергии идеального газа:

· Полная работа при изменении объема газа

где V₁ и V₂ – соответственно начальный и конечный объемы газа.

· Работа газа:

а) при изобарном процессе

, или ;

б) при изотермическом процессе

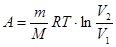, или ;

в) при адиабатическом процессе

, или ,

где T₁, T₂ и V₁, V₂ – соответственно начальные и конечные температура и объем газа;

– показатель адиабаты.

· Уравнение адиабатического процесса (уравнение Пуассона):

P×V ^g=const; T×V ^g^-1=const; T ^g× P ^1-^g=const.

· Термический КПД для кругового процесса (цикла)

где Q₁ – количество теплоты, полученное системой от нагревателя;

Q₂ – количество теплоты, отданное системой холодильнику;

A – работа, совершаемая за цикл.

· Термический КПД цикла Карно

где T₁ – температура нагревателя;

T₂ – температура холодильника.

· Изменение энтропии при равновесном переходе системы из состояния 1 в состояние 2:

Примеры решения задач

Пример 1. Определить для серной кислоты:

1) относительную молекулярную массу M_r;

2) молярную массу М.

Решение.

1. Относительная молекулярная масса вещества определяется по формуле ,

где n_i – число атомов i -го элемента, входящих в молекулу;

А_r,_i – относительная атомная масса i -го элемента.

Химическая формула серной кислоты имеет вид H₂SO₄. Следовательно, M_r=n₁A_r_,1+n₂A_r_,2+n₃A_r_,3.

Из формулы серной кислоты следует, что n₁ =2 (два атома водорода), n₂ =1 (один атом серы) и n₃ =4 (четыре атома кислорода). Значения относительных атомных масс водорода, серы и кислорода находим в таблице Д. И. Менделеева: A_r_,1 =1; A_r_,2 =32; A_r_,3 =16.

Тогда получим: M_r =2×1+1×32+4×16=98.

2. Молярную массу серной кислоты находим по формуле:

M=M_r ×10^-3 кг/моль.

Следовательно, M =98×10^-3 кг/моль.

Пример 2. В баллоне объемом 10 л находится гелий под давлением p₁ =1 MПа и при температуре Т₁ =300 К. После того, как из баллона было взято m =10 г гелия, температура в баллоне понизилась до T₂ =290 К. Определить давление p₂ гелия, оставшегося в баллоне.

Дано:	Решение:
V =10 л = 10^-2 м³ p₁ =1МПа=10⁶Па T₁ =300К m =10г=10^-2кг Т₂ =290К	Запишем уравнение Менделеева-Клапейрона для конечного состояния газа: , (1) где m₂ – масса гелия в баллоне в конечном состоянии;

М – молярная масса гелия (M =4×10^-3 кг/моль);

R – молярная газовая постоянная (R =8,31 Дж/моль×К).

Искомое давление:

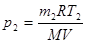. (2)

Массу m₂ гелия выразим через массу m₁, соответствующую начальному состоянию, и массу m гелия, взятого из баллона: m₂=m₁-m.

Из уравнения Менделеева-Клапейрона для начального состояния получаем: 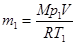. Тогда .

Подставив это выражение в уравнение (2), найдем:

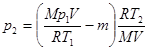, или .

Произведем вычисления:

Ответ: p₂ =0,364 МПа.

Пример 3. Найти среднюю кинетическую энергию <e _вр > вращательного движения одной молекулы кислорода при температуре Т =350 К, а также кинетическую энергию Е_к вращательного движения всех молекул кислорода массой m =4 г.

Дано:	Решение:
Т =350 К m =4 г=4×10^-3 кг	На каждую степень свободы молекулы газа приходится одинаковая средняя энергия ,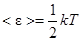
<e _вр >-? Е_к -?

где k – постоянная Больцмана;

Т – термодинамическая температура газа.

Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода

. (1)

Кинетическая энергия вращательного движения всех молекул газа

E_к =<e _вр >× N. (2)

Число всех молекул газа

N=N_A×n =N_A × , (3)

где N_A – постоянная Авогадро;

n – количество вещества;

m – масса газа;

М – молярная масса газа.

Подставив выражение (3) в формулу (2), получаем:

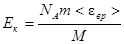. (4)

Произведем вычисления, учитывая, что для кислорода М =32×10^-3 кг/моль; k =1,38×10^-23 Дж/К; N_A =6,02×10²³ моль^-1:

<e>=1,38×10^-23×350 Дж = 4,83×10^-21 Дж,

Ответ: <e _вр >=4.83×10^-21 Дж; Е_к =364 Дж.

Пример 4. Кислород массой m =2 кг занимает объем V₁ =1 м³ и находится под давлением p₁ =0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V₂ =3 м³, а затем при постоянном объеме до давления p₃ =0,5 МПа. Найти изменение D U внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

Дано:	Решение:
m =2 кг V₁ =1 м³ p₁ =0,2 МПа=2×10⁵ Па p₁ =const V₂ =3 м³ V₂ =const p₃ =0,5 МПа=5×10⁵ Па	Изменение внутренней энергии газа , где i – число степеней молекулы газа (для двухатомных молекул кислорода i =5); D T=T ₃– T ₁ – разность температур газа в конечном (третьем) и начальном состояниях.
D U -? A -? Q -? p(V) -?

Начальную и конечную температуру газа найдем из уравнения Менделеева-Клапейрона :

и .

Тогда

Произведем вычисления:

Работа расширения газа при постоянном давлении (p ₁=const) выражается формулой A ₁ =p ₁×D V=p ₁(V ₂– V ₁). Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. А₂ =0. Следовательно, полная работа, совершенная газом:

А=А ₁ +А ₂ =А ₁ =p ₁(V ₂– V ₁).

Произведем вычисления:

A =2×10⁵×(3-1) Дж = 4×10⁵ Дж.

Согласно первому закону термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии DU и работы A: Q =D U + A. Следовательно,

Q =32,5×10⁵ Дж + 4×10⁵ Дж =

=36,5×10⁵ Дж =3,65 МДж.

График процесса приведен на рисунке 11.

Рис. 11

Пример 5. В цилиндре под поршнем находится водород массой m =0,02 кг при температуре T₁ =300 К. Водород сначала расширился адиабатно, увеличив свой объем в n₁ =5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n₂ =5 раз. Найти температуру в конце адиабатного расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.

Дано:	Решение:
M =0,02 кг Т₁ =300 К n₁ =5 n₂ =5	Температуры и объемы газа, совершающего адиабатический процесс, связаны между собой соотношением , (1)
T ₂-? A ₁-? A ₂-?

где g – показатель адиабаты, ;

i – число степеней свободы молекулы.

Для водорода как двухатомного газа i =5. Следовательно, . Так как , то , откуда

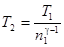. (2)

Работа А₁ газа при адиабатическом расширении может быть определена по формуле:

, (3)

где С_V – молярная теплоемкость газа при постоянном объеме;

М – молярная масса газа.

Работа А ₂ при изотермическом процессе может быть выражена в виде:

, или , (4)

где .

Подставляя числовые значения величин в выражения (2), (3) и (4), произведем вычисления, учитывая, что для водорода М =2×10^-3 кг/моль.

К.

(5^0,4= x; или lg x =0,4lg5=0,2796, тогда x =1,91; 5^0,4=1,91)

адиабата

= – 20998Дж= –21кДж.

Знак «–» показывает, что при сжатии работа газа совершается над газом внешними силами.

изотерма

График процесса представлен на рисунке 12.

Рисунок 12

Пример 6. Температура нагревателя тепловой машины 500 К. Температура холодильника 400 К. Определить КПД тепловой машины, работающей по циклу Карно, и полную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты.

Дано:	Решение:
T_н =500 К Т_х =400 К Q_н =1675 Дж t =1 c	КПД машины, работающей по циклу Карно, определяется по формуле , (1)
h-? N -?

или . (2)

Полная мощность машины

, (3)

или . (4)

Подставляя числовые значения в выражения (1) и (4), получим:

; h=20%.

Ответ: h=20%; N =335 Вт.

Пример 7. Найти изменение энтропии при переходе 8 г кислорода от объема 10 л при температуре 80°С к объему 40 л при температуре 300^оС.

Дано:	Решение:
m =8 г=8×10^-3 кг V₁ =10 л=10^-2 м³ T₁ =353 К V₂ =40 л=4×10^-2 м³ T₂ =573 К	Изменение энтропии: 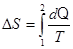. Согласно первому закону термодинамики d Q = dU + dA

где – изменение внутренней энергии газа;

dA = p × dV – работа газа при изменении объема.

Из уравнения Менделеева-Клапейрона находим давление газа . Тогда , а .

Следовательно

или .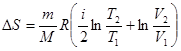

Произведем вычисления, учитывая, что для кислорода i =5; М =32×10^-3 кг/моль.

Ответ: D S = 5,4 Дж/К.

К о н т р о л ь н а я р а б о т а № 1

Вар.	Номера задач

101. Тело брошено вертикально вверх с начальной скоростью _o=4м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью _о вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.