1. Задаем матрицу системы А и матрицу свободных членов В. Для этого пишем А, вводим двоеточие (которое автоматически заменится на знак присваивания «:=»), затем на панели инструментов для работы с матрицами и векторами нажимаем кнопку создания матрицы или вектора 
и вводим матрицу системы. Аналогично вводим столбец свободных членов.
2. Вводим lsolve(A,B)=
Пример:
|
|
|
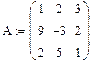
Решение с помощь функции Given…Find
1. Вводим начальные приближения: x1:=1, x2:=1, x3:=1.
2. Вводим слово Given
3. Ниже вводим систему уравнений, используя при этом вместо обычного знака равно знак булева равенства (вводится нажатием Ctrl+=).
4. Ниже пишем: Find(x1,x2,x3)=
Пример:
|
|
|
|
|
|
|
|
Решение СЛАУ методом обратной матрицы
1. Вводим матрицу системы и матрицу свободных членов, как и при решении с помощью lsolve().
2. Вводим x:=A-1B. Для ввода обозначения обратной матрицы нужно воспользоваться соответствующей кнопкой панели инструментов «Матрицы».
3. Вводим x=
Пример:
|
|
|
|
|
|
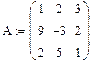
Решение нелинейных уравнений с помощью MathCad.
Локализация корней.
Предположим нам нужно уточнить корни уравнения f(x):=x cos(x).
Для локализации корней удобно построить график функции. Для этого нужно:
1. Определить функцию, т.е. ввести f(x):=x cos(x)
2. Выбрать Вставить-Графики-Зависимость XY.
3. Под осью абсцисс ввести х, слева от оси ординат ввести f(x).
4. При необходимости откорректировать пределы изменения аргумента и функции.
Основные свойства графика можно настроить выбрав пункт Формат в контекстном меню, вызываемом щелчком правой кнопкой мыши на графике.
В результате анализа графика определяются начальные приближения корней уравнения.
Уточнение корней.
Уточнение корней производится с помощью функции root():
1. Устанавливаем точность вычислений, изменяя значения пункта Порог сложности на закладке Толерантность окна, вызываемого командой Формат-Результат. На закладке Формат номера того же окна выбираем способ отображения результата и количество отображаемых десятичных знаков.
2. Вводим root(f(x),x)=
Пример:
|
|
|
|
Интерполирование функций средствами MathСad
В MathCad имеются средства для сплайновой интерполяции.
Интерполирование производится с помощью функции interp (vs,vx,vy,x), которая возвращает вектор значений функции y в интересующих точках х.
Здесь и далее vx – вектор исходных значений аргумента, vy – вектор исходных значений функции, vs – вектор вторых производных, возвращаемых одной из функций cspline (vx,vy), pspline (vx,vy), lspline (vx,vy), которые возвращают вектор vs при использовании кубических, параболических и линейных сплайнов соответственно.
Для интерполирования линиями можно воспользоваться функцией linterp(vx, vy, x).
Конечно, используя вычислительные возможности MathCad, всегда можно воспользоваться другим методом интерполяции (например, с помощью полиномов Ньютона и Лагранжа).
Пример.
Имеются экспериментально полученные точки:
| Значение аргумента x | Значение функции y |
| -1.06 -0.837 -0.684 -0.315 -0.117 -0.0 0.115 0.5 | 1.22 0.854 0.513 0.271 0.217 0.198 0.218 0.277 |
Построить график функции y(x) используя точки, отличные от экспериментально полученных.
Решение.
|
|
|
|
|
|
|
|
|
|
|
Аппроксимация зависимостей с помощью MathCad
В MathCad можно найти значения функции у в промежуточных точках с помощью полинома некоторой степени. Для этого используются следующие функции:
regress(vx,vy, k) – возвращает вектор, который использует функция interp для нахождения полинома степени k, который наилучшим образом приближает значения x и y данных, хранящихся в векторах vx, vy.
interp (vs,vx,vy, x) – возвращает приближенное значение y, соответствующее значению x. Где vs – вектор, получаемый с помощью regress.
Пример.
Имеются экспериментально полученные точки:
| Значение аргумента x | Значение функции y |
| 1,5 3,7 |
Определить вид аппроксимирующего полинома 4-й степени и с его помощью построить график функции y(x).
Решение.
Решим задачу методом наименьших квадратов, а затем с помощью встроенных функций MathCad.
| Введем исходные данные |
|
|
| Вычислим коэффициенты системы уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
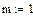
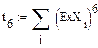
| Определим матрицу коэффициентов и матрицу свободных членов системы |
|
|
| Найдем коэффициенты полинома, решив систему |
|
|
| Определим вид полинома |
|
| Построим график Р(х) |
|
|
|
|
|
| Во всех точках х для сравнения вычислим значения функции с помощью встроенных средств аппроксимации |
|
|
| Строим графики |
|
Как видно, графики совпадают.
Вычисление определенного интеграла
и производной средствами MathCad
Предположим нужно вычислить интеграл функции 
на отрезке [0; 2] и производную этой функции в точке х=1. Решение такой задачи в MathCad имеет вид:
|
|
|
|
|
|
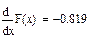
Интеграл может быть кратным, подынтегральная функция может быть комплексной или функцией нескольких переменных.
Для вычисления производных более высоких порядков используется специальная конструкция:
Решение ОДУ средствами MathCad
Для решения линейных обыкновенных дифференциальных уравнений в MathCad функция odesolve(x,b,[step]), которая возвращает значение функции, зависящей от х и являющейся решением линейного ОДУ. Здесь х – аргумент, b – правый конец отрезка, [step] – необязательный параметр, количество шагов для нахождения решения. Количество начальных условий должно равняться порядку уравнения.
Пример. Решим уравнение 
на отрезке [0, 4π]. Известно, что y(0)=0, а y’(0)=1.
Решение:
|
|
|
|
|
|
|
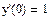
Примечание: В блоке Given используются знаки булева равенства, вставляемые нажатием Ctrl+= и знак производной (штрих), вставляемый нажатием Ctrl+F7.
Решение ОДУ первого порядка вида 
может быть получено с помощью функций rkfixed(y0,a,b,n,D), которая возвращает матрицу, состоящую из двух столбцов. В первом столбце хранятся значения аргумента, во втором – функции (результаты решения). Здесь y0 – начальное значение функции y, а – начало отрезка, b – конец отрезка, n – количество отрезков разбиения, D – первая производная от у.
Пример. Решим уравнение 
на отрезке [0, π]. Известно, что y(0)=1.
Решение:
|
|
|
|
|
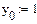
Для решения ОДУ первого порядка так же можно использовать функцию rkadapt(), аналогичную рассмотренной выше rkfixed(), за исключением того, что решение находится не с фиксированным шагом, а с автоматическим его подбором.
