Постановка задачи. Обыкновенные дифференциальные уравнения (ОДУ) или их системы часто используют для построения математических моделей динамических процессов.
Динамические процессы – процессы перехода физических систем из одного состояния в бесконечно близкое другое. Примерами таких процессов могут служить явления, возникающие в электрических сетях, распространение радиоволн, движение материальных точек, изменение химического состояния вещества и т.д.
Точные методы решения ДУ позволяют выразить решение через элементарные или специальные функции. Однако классы таких уравнений достаточно немногочисленны и охватывают малую часть возникающих на практике задач. В силу этого, важное значение приобретают приближённые численные методы решения ДУ.
Пусть требуется решить задачу Коши: y'(x) = f(x,y), y0=y(x0) – начальное условие, [ x0,xn ] – отрезок, 
.
Для решения ДУ n -ого порядка используют метод понижения производной, т.е. уравнение n -ого порядка сводят к системе n уравнений n -ого порядка способом замены переменных.
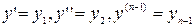
Методы решения одного уравнения 1-ого порядка распространяются на систему уравнений 1-ого порядка.
Сущность численных методов решения ДУ. На отрезке [ x0,xn ] выбирается некоторое множество точек. Это множество точек называется сеткой (x0<x1<x2<…<xn). В полученных точках вычисляются приближённые значения y1,y2,…,yn. Эти решения и будут являться решением задачи Коши. Величина 
– называется шагом сетки. В большинстве случаев h=const, xn=x0+kh.
Проблема численного решения ДУ заключается в построении алгоритма вычисления. Различают одношаговые и многошаговые методы решения ДУ. Метод Эйлера и метод Рунге-Кутта относятся к одношаговым. Многошаговые методы – это методы прогноза и коррекции. Для метода Адамса необходимо знать 2 предыдущие точки, для метода Милна – 3 точки. Их преимущество в том, что для них существует формула оценки погрешности.
Метод Эйлера. Различные методы группы методов Рунге-Кутта различаются друг от друга объёмом производимых вычислений и получаемой при этом точностью. Метод Эйлера является методом Рунге-Кутта первого порядка точности. Формула для вычисления методом Эйлера:
.
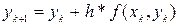Следовательно:
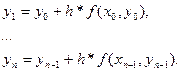
Метод Эйлера является наиболее простым, но и наименее точным. Он применяется для получения оценочных решений на небольшом интервале [ x0;xn ].
Метод Рунге-Кутта 4-ого порядка точности. Смещение из точки [ xk;yk ] в точку 
происходит не сразу, а через промежуточные точки. На практике наибольшее распространение получил метод 4-го порядка точности. Значение функции в i+1- й точке вычисляется следующим образом:
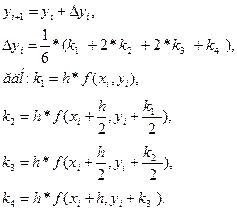
Метод Рунге-Кутта обладает достаточно высокой точностью, легко программируется, т.к. для вычисления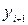 
нужно знать лишь одно значение yi. С помощью этого метода можно начинать решение ДУ. Величину шага изменения аргумента х можно легко менять на любом этапе вычисления.
Недостатки:
1) Необходимость 4 раза вычислять значение функции на каждом шаге.
2) Отсутствие легко определяемой оценки ошибки метода.
Для оценки правильности шага рассчитывают: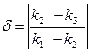 
, которое должно быть меньше либо равно 0,05. В противном случае шаг следует уменьшить в 2 раза, провести вычисления и снова оценить δ.
Метод Рунге-Кутта имеет порядок точности, сопоставимый со значением шага взятым в 4-ой степени. Для оценки погрешности метода пользуются формулой Рунге: 
ЗАДАНИЯ
1. Разработать схемы алгоритмов решения обыкновенного дифференциального уравнения методами Эйлера и Рунге-Кутта IV порядка точности.
2. В среде Delphiсоздать приложение для решения дифференциальных уравнений, приведенных в табл.5 (в соответствии со своим вариантом) методами Эйлера и Рунге-Кутта IV порядка.
3. Решить дифференциальное уравнение (в соответствии со своим вариантом) с помощью MathCad.
4. Вычислить погрешности методов решения дифференциальных уравнений.
5. На основании результатов п.п. 2, 3, 4 провести сравнительный анализ методов численного решения дифференциальных уравнений.
Таблица 5
| Вариант | Уравнение | Начальные данные | Отрезок интегрирования |
| 
| 
| |
 
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
|
| 
| |
|
| 
| |
| 
|
| |
|
|
|
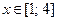
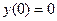
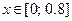
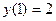
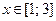
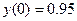
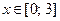
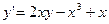
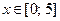
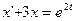
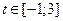
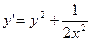
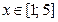
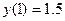
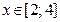
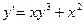
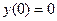
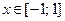
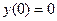
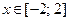
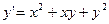
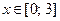
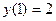
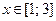
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что является решением дифференциального уравнения?
2. Почему для решения дифференциального уравнения необходимо иметь начальные условия?
3. Зачем дифференциальное уравнение преобразуют к виду y'=f(x,y)?
4. Почему метод Рунге-Кутта IV порядка точнее метода Эйлера?
5. За счет чего возникает погрешность в методе Эйлера? Как ее уменьшить?
6. Как выбирается шаг интегрирования в методе Рунге-Кутта IV порядка точности?
Литература
Основная литература.
1. Алексеев В.Е. Вычислительная техника и программирование. Практикум по программированию / В.Е. Алексеев, А.С. Ваулин, Г.Б. Петрова: Под редакцией А.В. Петрова – М.: Высш. шк., 1991.
2. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике, Уч. пос. для техн., М: Высш. шк., 1990.
3. Волков Е.А. Численные методы: Уч. пос. для ВУЗов. М: Наука, 1987.
4. Вычислительная техника и программирование: Учебн. Для техн. ВУЗов/А.В. Петров, В.Е. Алексеев, А.С. Ваулин и др.; Под ред. А.В. Петрова. – М.: Высш. Шк.,1990.
5. Гусак А.А. Математический анализ и дифференциальные уравнения: справочное пособие / Изд. 2-е, - Мн.: «Тетрасистем», 2001
6. Дьяконов В. MathCad 2001: Специальный справочник. – СПб.: Питер, 2002.
7. Кренкель Т.Э. и др. Персональные ЭВМ в инженерной практике: Справочник / Т.Э. Кренкель, А.Г. Кочан, А.М. Тараторин. –М.:Радио и связь, 1989.
8. Методические указания к выполнению курсовой работы «Вычислительная техника, программирование и математическое моделирование» для студентов -заочников машиностроительных специальностей. БГПА, Мн. – 1994.
9. Справочное пособие по приближенным методам решения задач высшей математики. \ Л. И. Бородич, А.И. Герасимович, М: Высш. шк., 1986.
Дополнительная литература.
1. Задачи и упражнения по математическому анализу. Под ред. Б. П. Демидовича. – М.: Наука, 1978. – 480 с.
2. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1984.
3. Фурунжиев Р. И., Бабушкин Ф. М., Варавко В. В. Применение математических методов и ЭВМ: Практикум: Учеб. пособие для вузов. – Мн.: Выш. шк., 1988.
4. Туркина Е.П. Математическая обработка данных с помощью пакета MathCad: Сб. лаб. работ. Для ст. эк. спец. – Мн.: БГЭУ, 2002.
Приложения
Решение СЛАУ средствами MathCad
MathCad – это программная среда для выполнения на компьютере разнообразных математических и технических расчетов, предоставляющая пользователю инструменты для работы с формулами, числами, графиками и текстами, снабженная простым в освоении графическим интерфейсом.
Окно программы имеет стандартный для Windows – приложений вид. Строка меню содержит следующие пункты: Файл, Редактирование, Вид, Вставка, Формат, Инструменты, Символы, Окно, Справка.
Включение необходимых панелей инструментов производится в Вид-Панели инструментов.
