Постановка задачи. В практике научных и инженерных расчётов возникает необходимость в решении нелинейных уравнений вида 
. Функция определена и непрерывна на некотором конечном или бесконечном интервалах.
Если функция представляет собой многочлен, то такое уравнение называется алгебраическим.
Если х находится под знаком трансцендентной функции (логарифмическая, показательная, тригонометрическая и т.д.), то в таких случаях уравнение называется трансцендентным.
Если известно значение x *, при котором выполняется условие 
, то х* называется корнем уравнения. Такой корень геометрически представляет собой абсциссу точки пересечения (или касания) графика функции 
с осью Оx. Будем также полагать, что уравнение имеет лишь изолированные корни, т.е. для каждого из корней существует окрестность не содержащая других корней этого уравнения. В общем случае уравнение не имеет аналитического решения. Т.к. на практике встречаются уравнения, содержащие коэффициенты с приближёнными значениями, то для решения такого уравнения используют численные приближённые методы, которые позволяют определять приближённое значение корней с заданной точностью.
Процесс решения нелинейного уравнения состоит из двух этапов:
1. Этап отделения корней, на котором производится установление количества корней и поиск интервалов, внутри которых содержится по одному изолированному корню уравнения.
2. Этап уточнения значений корней, на котором значения отдельных корней уточняются одним из известных методов до некоторой заданной степени точности.
Методы отделения корней.. Мы ограничимся рассмотрением методов поиска лишь действительных корней. Существует 2 способа отделения корней.
1. Графический способ заключается в обнаружении точек пересечения графика функции с осью Ох. Абсциссы точек пересечения и выбираются в качестве начальных приближённых значений корней.
Часто уравнение можно привести к виду 
. Тогда отделить корни можно построив графики функций 
и 
и обнаружив точки их пересечения.
2. Численный способ отделения корней основывается на следующем критерии. Если функция 
непрерывна на отрезке AB и принимает на концах этого отрезка значения противоположных знаков, а производная функции на отрезке AB сохраняет постоянный знак, то внутри отрезка существует корень уравнения и при этом единственный.
Алгоритм численного отделения корней:
1. Найти производную функции 
.
2. Найти критические точки функции .
3. Составить таблицу знаков функции на границах отрезка AB и в критических точках.
4. Определить отрезки, на концах которых функция принимает значения противоположных знаков.
5. Выбрать в качестве начальных приближенных значений корней по одному произвольному (если метод уточнения корней, который планируется использовать не налагает каких-либо дополнительных условий) значению х внутри каждого отрезка, найденного в п.4.
Следует отметить, что универсальных способов отделения корней, пригодных для любых уравнений, не существует
Приближённые значения корней уточняют различными итерационными методами. Под итерационным методом подразумевается построение числовой последовательности корней, сходящихся к искомому корню х*.
Одной из важнейших характеристик итерационного метода является его скорость сходимости.
Говорят, что последовательность 
, сходящаяся к пределу х* имеет порядок сходимости α, если существуют числа 
и 
,такие, что для любого 
выполняется неравенство:
.
При 
сходимость называется линейной, при 
- квадратичной, а при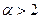 
- сверхквадратичной. Чем больше порядок сходимости, тем сложнее вычислительный алгоритм, но тем выше скорость сходимости итерационной последовательности.
Метод деления отрезка пополам. Для применения этого метода функция должна быть непрерывна и ограниченанаотрезке AB, внутри которого имеется корень. Значения функции на концах отрезка при этом должны имеют разные знаки 
.
Суть метода.
1. Отрезок АВ делят пополам и находят начальное приближение корня 
;
2. Если 
, то х 0 – корень уравнения, иначе из отрезков [ а; х 0] и [ х 0; b ] выбирают тот, на концах которого функция имеет разные знаки, и который, следовательно, содержит искомый корень. Выбор интервала сводится к проверке двух условий. Если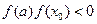 
, то корень расположен на отрезке [ а; х 0], если 
, то корень расположен на отрезке [ х 0; b ].
3. Найденный интервал, который в большинстве случаев удобно вновь переобозначить как [ а; b ], вновь делят пополам и выполняют поиск отрезка, содержащего корень и т.д. Если требуется определить корень с точностью ε, то деление пополам продолжают до тех пор, пока длина отрезка не станет меньше 2 ε. В этом случае середина последнего отрезка и есть корень с требуемой точностью.
Метод деления отрезка пополам всегда сходится.
Метод последовательных приближений. Часто этот метод называют методом простых итераций. Для данного метода уравнение должно быть представлено в итерационном виде 
.
Суть метода.
В качестве начального приближения корня х 0выбирают любую точку, расположенную внутри отрезка [ a; b ]. Последующие приближения вычисляются с помощью итерационной процедуры:
;
...
, k = 0, 1, 2, …
Процесс продолжают до тех пор, пока не будет найдено приближенное значение корня, имеющее заданную точность.
Теорема сходимости итерационного процесса: если интервал (a,b) является интервалом изоляции корня уравнения и во всех точках этого интервала 
|, то итерационный процесс сходится. Вычисления прекращаются при выполнения условия 
, где ε – заданная абсолютная погрешность вычисления корня.
Преобразование уравнения к виду можно произвести разными способами, простейшие из них:
1. Выделяют x из , а все остальное переносят в правую часть.
2. Выполняют преобразование 
, где с – произвольная постоянная. Тогда 
. Подбором величины с добиваются получения возможного меньшего значения константы q.
Погрешность метода на k и k- 1 итерации: 
.
Метод последовательных приближений имеет преимущество в том, что при его использовании не накапливается погрешность вычисления. Любое найденное x k можно использовать в качестве нового начального приближения. Т.е. если в процессе вычислений допускались ошибки, то они не влияют на окончательный результат, если заданная погрешность нахождения корня существенно превышает погрешность вычислений (в т.ч. машинных). Это свойство метода последовательных приближений делает его наиболее надежным методом уточнения корней.
Метод касательных (метод Ньютона). Пусть на отрезке [ a; b ] имеется корень уравнения , функция на этом отрезке непрерывна, а производные функции 
и 
определены, непрерывны и сохраняют постоянные знаки. Таким образом, на отрезке [ a; b ] функция монотонна и не меняет характера выпуклости.
Суть метода.
Выбирают начальное приближение корня x 0, в качестве которого удобно взять конец отрезка [ a; b ] для которого 
(в противном случае сходимость метода Ньютона не гарантируется). Далее проводят касательную в точке C0 к кривой 
, до пересечения с осью абсцисс. Абсциссу х 1 принимают за очередное приближение корня. Каждое последующее приближение определяется из рекуррентного соотношения:
.
Для оценки расстояния очередного приближения х k до корня х* воспользуемся следующими рассуждениями. В соответствии с формулой Лагранжа 
получаем, что 
. О точке с известно лишь то, что она находится между х k и х*. Поэтому оценка погрешности возможна с помощью следующего соотношения:
,
где 
.
Метод Ньютона имеет квадратичную сходимость. Иногда, если сложно выбрать начальное приближение, то начинают решение методом деления отрезка пополам (т.е. берут середину отрезка) и продолжают уточнять с помощью метода Ньютона.
Метод хорд. При реализации метода касательных, при каждой итерации нужно вычислять значение как функции , так и её первой производной. Существует вариант метода Ньютона – метод хорд (секущих), который позволяет избежать вычисления производной. Рекуррентное соотношение для вычисления приближенных значений корня в этом методе имеет вид:
.
В качестве с выбирается конец отрезка (точка а или b) для которого выполняется условие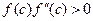 
. В качестве начального приближения х 0 выбирается конец отрезка, оставшийся после выбора с (если с=b, то х 0= а и наоборот).
Оценка степени приближения к корню производится также как и при использовании метода касательных.
Название методу было дано из-за его геометрического смысла: если 
, а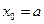 
, то следующее приближение корня х 1 соответствует точке пересечения хорды, соединяющей концы кривой, с осью абсцисс. Далее на кривой находится точка с абсциссой х 1, проводится следующая хорда и т.д.
Этот метод, как и метод касательных также имеет квадратичную сходимость.
Сравнение методов. Наибольшей универсальностью обладает метод деления отрезка пополам. С его помощью можно решить любое уравнения вида , если его корни изолированы, а функция на отрезках, содержащих корни непрерывна. Методы последовательных приближений, касательных и хорд предъявляют к функции более жёсткие требования. Сходимость этих методов зависит от выбора начального приближения корня. При реализации этих методов необходимо вычислять производные этих функций для организации итерационного процесса и выполнять проверку условия сходимости.
Методы деления отрезка пополам и последовательных приближений имеют линейную сходимость, а методы касательных и хорд – квадратичную.
При выборе метода уточнения корней нужно помнить, что скорость сходимости и быстрота решения задачи – вещи совершенно разные. Поэтому при привлечении ЭВМ для решения нелинейных уравнений, часто использование более простого метода с малой скоростью сходимости, например, метода деления отрезка пополам, может дать результат гораздо быстрее, чем использование изощренного и сложного для понимания и программирования метода уточнения с высокой скоростью сходимости.
ЗАДАНИЯ
1. Разработать алгоритмы решения нелинейных уравнений методами: деления отрезка пополам, хорд, касательных (Ньютона).
2. Найти решения нелинейных уравнений, приведенных в таблице 2 (в соответствии со своим вариантом), с использованием функции root(..) математического пакета MathCad.
3. Средствами Delphi создать приложение для решения нелинейных уравнений, приведенных в таблице. Начальные приближения корней выбрать из указанных областей.
4. Оценить полученные результаты, сделать вывод.
Примечание: Погрешность полученных решений не должна превышать ε= 0,0001.
Таблица 2
| Вариант | Уравнение | Область, содержащая корень | Методы решения |
| [0; 2] | Касательных | |
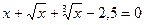
| [0.4; 1] | Деления пополам | |
| [0; 0.85] | Хорд | |
| [1; 2] | Деления пополам | |
| [0; 0.8] | Хорд | |
| [1.2; 2] | Касательных | |
 
| [3; 4] | Деления пополам | |
| [-1; 1] | Хорд | |
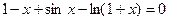
| [0; 1.5] | Касательных | |
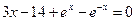
| [1; 3] | Деления пополам | |
| [0; 1] | Хорд | |
| [0.5; 1] | Касательных | |
| [1; 3] | Деления пополам | |
| [0; 1] | Хорд | |
| [2; 3] | Касательных | |
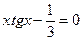
| [0.2; 1] | Деления пополам | |
| [1; 2] | Хорд | |
| [1; 2] | Касательных | |
| [0; 1] | Деления пополам | |
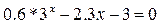
| [2; 3] | Касательных | |
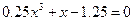
| [0; 2] | Хорд | |
| [2; 4] | Касательных | |
|
| [3; 4] | Хорд | |
| [0; 6] | Деления пополам | |
| [-2; 2] | Деления пополам | |
| [2; 3] | Хорд | |
| [0; 1] | Касательных | |
|
| [2; 3] | Деления пополам | |
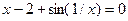
| [1.2; 2] | Хорд | |
|
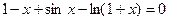
| [0; 1.5] | Касательных | |
| [2; 3] | Касательных | |
| [0; 0.85] | Хорд | |
| [2; 3] | Деления пополам | |
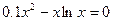
| [1; 2] | Касательных | |
|
| [0.5; 1] | Хорд | |
| [0; 1] | Деления пополам |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие методы решения нелинейных алгебраических уравнений Вы использовали при выполнении работы?
2. Какой метод отделения корней Вы применяли?
3. Опишите алгоритм уточнения корней методом:
а) половинного деления;
б) хорд;
в) касательных (Ньютона).
4. Проведите сравнительный анализ различных методов решения нелинейных уравнений.
