Постановка задачи. На практике в результате экспериментальных исследований часто получают набор значений некоторой величины у, при фиксированных значениях второй величины x. Аналитическая зависимость между значениями х и у чаще всего неизвестна, что не позволяет, например, вычислить значение величины у в промежуточных точках, отличных от полученных экспериментально. Для нахождения значений в этих промежуточных точках строят приближённую функцию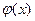 
. Значения функции 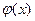в имеющихся точках х либо совпадают, либо приближены к экспериментально наблюдаемым значениям у в этих точках. Построение функции 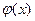называется интерполированием. Т. о. график функции 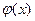должен проходить через все экспериментально полученные точки (х i, y i).
К интерполированию прибегают и в тех случаях, когда аналитический вид некоторой функции 
известен, но получение её значений в нужных точках требует громоздких вычислений. Чтобы этого избежать, функцию также заменяют приближённой функцией .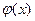
В качестве приближенной функции 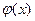часто используется алгебраический многочлен (полином), вида:
.
Объясняется это тем, что сравнительно просто автоматизировать вычисления коэффициентов многочлена, просто его интегрировать и дифференцировать. Наряду с многочленами для аппроксимации используют элементарные функции и ряды Фурье.
Интерполяционный многочлен Лагранжа. Интерполяционный многочлен Лагранжа степени n, принимающий в точках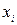 
отрезка [ a; b ] значения 
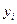, где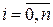 
имеет вид:
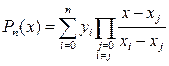
или:
.
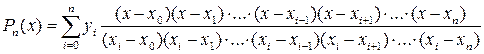Погрешность интерполяции определяется разностью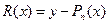 
.
Таким образом, значение функции у в точке х, отличной от заданных хi, может быть вычислено по формуле:
.
Эту функцию называют функцией Лагранжа.
Интерполяционный многочлен Ньютона. Интерполирование по формуле Лагранжа имеет следующие недостаток: в этой формуле каждое слагаемое представляет собой многочлен n -ой степени. Следовательно, при увеличении числа точек х i и, соответственно, y i увеличивается степень многочлена Лагранжа, и т.к. каждое его слагаемое зависит от всех значений аргумента х, то вычисление полинома Лагранжа необходимо производить заново. Указанного недостатка нет при вычислении полинома Ньютона.
Введём понятие разделённых разностей.
Разделёнными разностями 1-го порядка называются значения: 
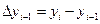- называется конечными разностями 1-го порядка.
Разделёнными разностями 2-го и более высоких порядков называют:
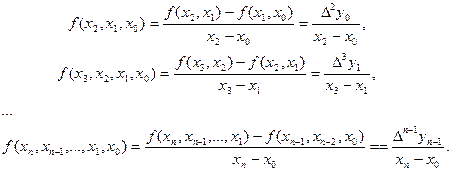
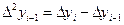- конечная разность 2-ого порядка и т.д.
С учётом введённых обозначений интерполяционный многочлен Ньютона имеет вид:
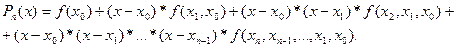
Погрешность:
Т.к. любой i-ый член полинома Ньютона зависит только от первых i-ых точек хi -ых и от значения функции в них добавление новых точек вызывает лишь добавление новых слагаемых без изменения первоначальных.
Аппроксимация функций методом наименьших квадратов. Аппроксимация является частным случаем интерполирования и применяется для определения аналитического вида функции заданной таблично. Задача аппроксимации сводится к определению свободного параметра (параметров) функции заданного вида, который обеспечит наилучшее приближение функции заданной таблично модельной аналитической функцией.
Метод наименьших квадратов.
Пусть таблично задана функция 
. Определить аппроксимационный многочлен вида
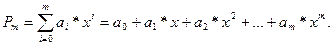(1) (1)
Для определения коэффициентов 
(где i=1,2…m) используют аппроксимацию методом наименьших квадратов. Функционал находится по формуле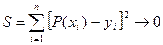 
, где n – количество пар значений аргумента xi и функции yi. Т.к. S должен быть минимален, то первые частные производные от S по всем коэффициентам полинома должны равняться нулю.
Вычислим их и приравняем к нулю:
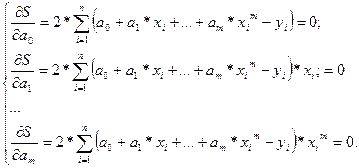(1)
После преобразования система слегка упростится:
(2) (2)
Если полином первой степени, то 2 уравнения, если шестой степени, то 7 уравнений. Введём следующие обозначения:
С учётом этих обозначений система (2) перепишется следующим образом:
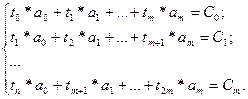(3)
Решив эту систему одним из известных методов определится ряд значений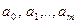 
, с помощью которого и строится многочлен (1).
Среднеквадратичное отклонение вычисляется по формуле:
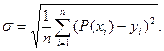
ЗАДАНИЯ
1. Разработать схемы алгоритмов интерполирования функций по методам Лагранжа, Ньютона, наименьших квадратов.
2. Произвести интерполирование и аппроксимацию табличных функций, приведенных в табл. 3 (в соответствии со своим вариантом), на отрезке [a, b] с шагом h средствами MS Excel и MathCad. Средствами Delphi создать приложение, решающее аналогичную задачу.
3. По результатам выполнения п.2 построить графики функций.
4. Произвести сравнительный анализ полученных результатов.
Таблица 3
| Вариант | Значение аргумента x | Значение функции y | Пределы изменения аргумента [a; b] | Шаг интерполи-рования h |
| -1.06 -0.837 -0.684 -0.315 -0.117 -0.0 0.115 0.5 | 1.22 0.854 0.513 0.271 0.217 0.198 0.218 0.277 | [-0.8; 0.4] | 0.2 | |
| -2.15 -1.83 -1.62 -1.45 -1.01 -0.72 -0.48 0.0 | -2.23 -2.65 -3.1 -3.54 -4.26 -4.38 -4.52 -4.27 | [-1.95; 0.1] | 0.3 | |
| -0.21 -0.143 -0.099 -0.032 0.114 0.182 0.257 0.38 | -12.64 -11.05 -10.25 -9.32 -9.25 -10.0 -11.48 -14.4 | [-0.2; 0.28] | 0.08 | |
| 0.215 0.441 0.638 0.865 1.05 1.30 1.55 1.82 | 5.82 4.63 4.10 3.34 3.0 3.29 4.32 5.72 | [0.4; 1.6] | 0.2 | |
| -1.0 -0.96 -0.86 -0.79 0.22 0.50 0.93 1.10 | -1.00 -0.151 0.894 0.986 0.895 0.50 -0.306 -0.51 | [-0.98; 1.02] | 0.35 | |
| 0.50 0.75 1.00 1.25 1.50 1.75 2.00 2.25 | 0.1915 0.2734 0.3413 0.3944 0.4332 0.4599 0.4773 0.4878 | [0.625; 2.126] | 0.25 | |
| 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 | -0.24 -0.24 -0.16 0.0 0.24 0.56 0.96 1.44 | [1.5; 2.7] | 0.2 | |
| 0.43 0.48 0.55 0.62 0.70 0.75 0.78 0.81 | 1.64 1.73 1.88 2.03 2.23 2.36 2.41 2.78 | [0.5; 0.6] | 0.02 | |
| [68; 72] | 0.5 | |||
| -2.0 3.0 4.5 12.0 15.0 18.5 20.0 23.0 | -17.0 -3.0 1.2 1.8 3.0 4.5 7.0 9.1 | [9.8, 11] | 0.2 | |
| -2.3 0.0 1.1 4.8 7.3 9.2 11.4 13.0 | -12.5 8.6 13.4 15.1 21.4 24.2 28.3 32.1 | [1.5, 3] | 0.5 | |
| 2.34 5.16 7.03 8.42 9.61 10.12 11.35 12.12 | 15.16 25.03 32.18 37.11 44.82 51.62 50.13 73.16 | [3; 6] | 0.5 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Аппроксимация и интерполирование функций. Постановка задачи.
2. В чем особенность аппроксимации?
3. Опишите особенности метода наименьших квадратов в случае линейной и квадратичной зависимости.
4. Какой из методов полиномиальной зависимости даёт более точный результат в вашем варианте лабораторной работы?
5. Интерполяционный многочлен Лагранжа, его преимущества и недостатки.
6. Интерполяционный многочлен Ньютона, его разновидности.
7. Оценка погрешностей методов Лагранжа и Ньютона.
