Нехай функція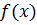 
– неперервна і невід’ємна на проміжку 
. Формула (2) з геометричної точки зору означає, що площа криволінійної трапеції = площі прямокутника за такой ж основою, що і у криволінійної трапеції і з висотою 
.
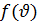Властивість 10. Узагальнена формула середнього значення
Нехай виконані умови:
1. Функція f(x), а також функція 
– інтегровані на проміжку 
.
2. 
3. 
, тобто на проміжку функція 
не змінює знак.
Тоді - 
(1) (якщо покласти 
, отримаємо формулу з вл. 9).
Доведення:
і будемо вважати, що 
. З другої умови теореми випливає, що 
виконується нерівність:
(2)
Якщо помножимо нерівність (2) на функцію , то отримаємо:
(3)
З цього слідує, що:
(4)
Якщо 
, то 
1. Якщо 
, то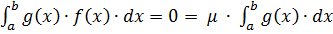 
. Отже за 
ми можемо взяти будь-яке число з 
;
2. Якщо 
. Розділивши нерівность (4) на 
одержимо: 
(5). Отже,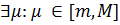 
. Покладемо у нерівності (5), що 
Перший випадок доведено.
2) У всіх інших випадках формула (1) залишається правильною, оскільки зміна знаку функції з «+» на «-», а також зміна меж інтегрування на протилежні з на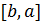 
не змінює формулу (6).
Зауваження:
Якщо умови теореми виконані і функція 
неперервна на , то формулу (1) можна подати у вигляді:
, де 
.
ВИЗНАЧЕНИЙ ІНТЕГРАЛ ЗІ ЗМІННОЮ ВЕРХНЬОЮ МЕЖЕЮ
Зауваження:
У визначеному інтегралі змінну інтегрування можна позначати будь-якою літерою або буквою, тобто має місце рівність::
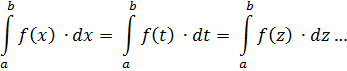
Нехай функція інтегрована на 
буде інтегрована на 
, де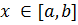 
тобто змінна 
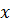– верхня межа.
Визначений інтеграл, що має вигляд 
називається визначеним інтегралом функції 
зі змінною верхньою межею.
Властивість 1.
Якщо функція 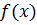інтегрована на проміжку , то Ф(
неперервна на .
Доведення:
Нехай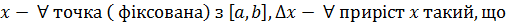 
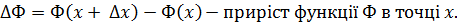Введемо позначення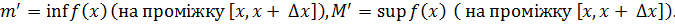 
Розглянемо приріст функції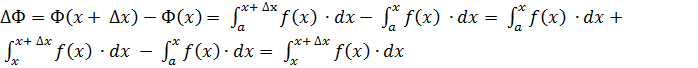 
.
Якщо застосувати формулу середнього значення, то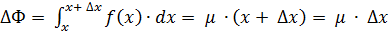 
(*), де 
.
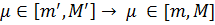Якщо в рівності (*) перейти до границі, коли 
, то одержимо: 
. А це означає, що функція 
– неперервна в точці 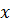. Оскільки точка 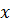була обрана довільно, то Ф 
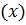– неперервна на .
Властивість 2.
Якщо функція – інтегрована на проміжку і неперервна в точці 
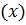. Тоді функція Ф диференційована в точці .
Доведення:
Нехай умови нашого твердження виконано тоді з рівності (*) (властивості 1):
(1)
Де 
. Оскільки функція – неперервна в точці , то це означає, що 
буде виконуватись нерівність:
виконується нерівність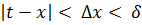 
а значить і:
Причому 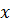– фіксована 
– змінна 
(2)
Одержимо 
,
Якщо перейти до границі в рівності (1), то одержимо 
. Це означає, що функція Ф 
має похідну в точці 
яка дорівнює .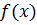
Наслідок:
Якщо 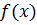– неперервна в 
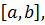то Ф( диференційована на . Тобто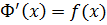 
. Це означає, що 
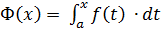можна розглядати як первісну 
.
ФОРМУЛА НЬЮТОНА-ЛЕЙБНІЦА
Нехай функція 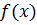– неперервна на , тоді має місце наступна формула Ньютона-Лейбніца:
Де 
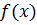– будь-яка з первісних функції на .
Доведення:
Нехай функція 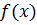– неперервна на , тоді згідно з наслідком до другої властивості інтеграла зі змінно верхньою межею функція 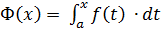є первісною 
. 
– будь-яка інша первісна. Тоді згідно із твердженням про первісні функції одержимо, що:
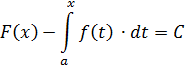
Покладемо 
:
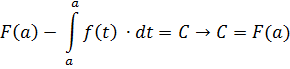
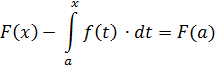
Покладемо 
:
Метод інтегрування частинами
Нехай функції u(x), v(x), u´(x), v´(x) неперервні на [a,b]. Тоді має місце наступна формула:
- 
або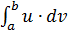 
= 
- 
.
Доведення:
За допомогою правила диференціювання добутку можна отримати рівність: 
Ця рівність означає,що функція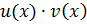 
є первісною для 
. Оскільки остання функція є неперервною на проміжку [a,b], то за допомогою формули Ньютона - Лейбніца одержимо, що 
= . З останньої рівності безпосередньо випливає формула (1):
= 
- 
.
Приклад
= 
= 
- 
= 
= 
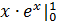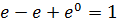
Заміна змінної у визначеному інтегралі
Теорема
Нехай виконуються умови:
Функція 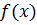неперервна на [a,b].
Функція 
, а також 
неперервні на проміжку [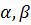 
]. Причому 
t 
[ 
] виконується нерівність a ≤ 
≤ b, тобто значення функції 
не виходить за межі проміжку [a,b].
=a, 
=b. Тоді має місце наступна формула:
= 
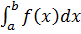(1)
Доведення
Нехай виконуються умови теореми. Оскільки функція 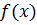неперервна на [a,b], то за допомогою формули Ньютона- Лейбніца, одержимо:
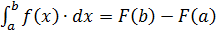(2), де - будь-яка первісна для . Оскільки неперервна на [a,b], то згідно з наслідком до другої властивості інтеграла зі змінною верхньою межею, цей інтеграл (який є однією з первісних для 
) є диференційованою функцією. Тому будь-яка інша первісна, у тому числі , диференційована на [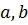 
], 
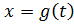диференційована на проміжку. Тоді 
диференційована [α,β]. Причому виконується рівність:
= 
Остання рівність означає, що 
- первісна для 
. Оскільки остання функція є неперервною на проміжку [ 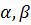], то згідно з формулою Ньютона – Лейбніца, одержимо наступну рівність:
= 
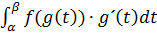(3)
(за третьою умовою теореми)
Порівнюючи рівності (2) і (3) одержимо рівність (1), що і треба було довести.
Якщо при обчисленні визначеного інтеграла зроблена заміна, то при знаходженні цього інтеграла немає потреби повертатися до вихідної заміни.
