Нехай функція f(x) визначена на деякому проміжку Х.
Означення. Функція F(x) називається первісною для функції f(x) на деякому проміжку Х, якщо F(x) диференційована на проміжку Х, причому виконується рівність F'(x) = f(x).
Теорема. Нехай F1(x) і F2(x) – довільні первісні для функції f(x) на проміжку Х, тоді F1(x) - F2(x)= сonst =C. Тобто дві первісні відрізняються одна від одної лише на сталу величину.
Доведення:
Нехай F1(x) і F2(x) первісні для функції f(x) на проміжку Х 
F1’(x) - F2’(x)= f(x) за означенням.
Позначимо F1(x) - F2(x)=λ(x).
Знайдемо похідну λ’(x) = F1’(x) - F2’(x) = f(x)- f(x)=0 (на проміжку Х).
А тоді з теореми про необхідну і достатню умову сталості функції одержимо, що λ(x)= сonst =C F1(x) - F2(x) = C.
Наслідок. Якщо F(x)- одна з первісних для функції f(x) на проміжку Х, то будь-яку іншу первісну Ф(x) цієї функції на цьому ж проміжку можна подати в такому вигляді Ф(x)=F(x)+C, де С – деяка стала.
Означення. Сукупність всіх первісних для функції f(x) на деякому проміжку Х називається невизначеним інтегралом функції f(x) на деякому проміжку Х і позначається 
, х- змінна інтегрування, 
- підінтегральна функція, 
- підінтегральний вираз,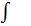 
- знак інтеграла.
Таким чином має місце рівність: = F(x)+С, де F(x) – одна з первісних для функції , С – будь-яка стала.
Приклад 1. 
,
= 
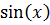, F(x) = 
, F'(x)= (
Властивості невизначеного інтеграла
1. 
Тобто знак диференціала і інтеграл взаємоскорочувані, якщо знак диференціала стоїть поперед знака інтеграла.
Оскільки $ , то виконується рівність (1) = F(x)+С (α), де F'(x) = f(x) (β).
.
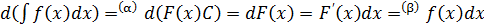2. 
.
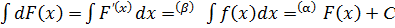3. Лінійна властивість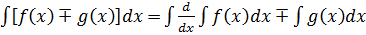 
,
[ 
= 
= 
4. Лінійна властивість 
= c , (c - const)
Доведення аналогічно вл. 3.
Таблиця інтегралів для деяких елементарних функцій
 (
| 
|
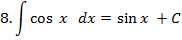
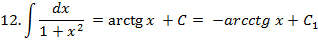
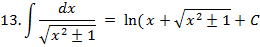
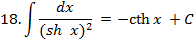
Найпростіші правила інтегрування
1. Якщо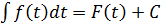 
(1), то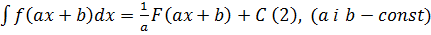 
З (1)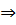 
F’(t) = f(t), З (2) [ 
]’= 
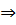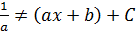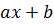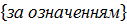F’(
) 
= f()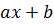
Приклад 1.
.
.
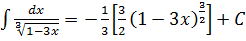2. 
[ 
]’ = 
Приклад. 
{ 
+ C.
Зауваження:
Інтеграли від елементарної функції не завжди можна виразити через елементарні функції. Якщо інтеграл вдається виразити через елементарні функції, то кажуть, що дана функція інтегрується в скінченому вигляді або в елементарних функціях.
Інтеграли, що не мають значень:
Інтеграл Пуасона: 
; Інтеграли Френеля: 
, 
, 
, 
, 
.
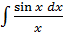Метод інтегрування частинами
Теорема. Нехай функції u(x) i v(x) диференційовані на деякому проміжку Х. Якщо існує первісна для функції v(x)* u’(x) на Х (тобто $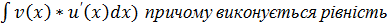 
або у скороченому вигляді 
(1’)
Доведення. Розглянемо 
. Застосуємо правило обчислення похідної: [ ]’ = 
+ 
(2)
Оскільки за умовою теореми $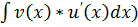 
, крім того за властивістю 1 невизначеного інтеграла 
= 
$ 
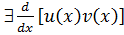. Тоді з рівності (2) одержимо формулу (1) (Беручи до уваги, що це рівність множин).
Приклад.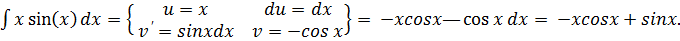 
Метод заміни змінної
Теорема. Нехай виконуються умови:
1) Функція t=φ(x) визначена і диференційована на проміжку Х, Т – множина значень функції φ(x).
2) Функція g(t) має первісну G(t) на T (тобто $ 
, тоді скалярна функція 
– первісна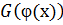 
на Х. 
(1).
Доведення. Нехай умови теореми виконані.
Знайдемо похідну правої частини формули (1) [ 
]’= G’(
.
Застосування. В багатьох випадках вдається підібрати t=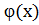 
, так що виконується рівність f(x)dx = 
. Причому 
.
Достатньо просто обчислити, будемо вважати, що 
. Тоді маємо 
= 
= 
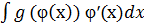Приклад. 
= 
Іноді заміну змінної проводять безпосередньо
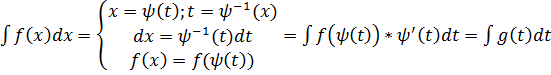
Припустимо, що інтеграл вдалось знайти і він має вигляд 
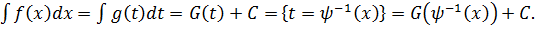
Приклад.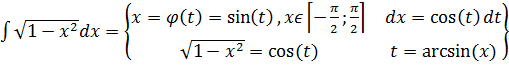 
= 
