Інтегрування многочленів
Нехай задана функція f(x)=anxn+an-1xn-1+…+a1x+a0= 
, (ai є R)
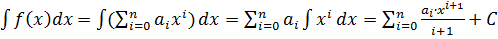
Інтегрування найпростіших елементарних дробів
Найпростішими елементарними дробами називаються наступні функції:
a. 
b. 
c. 
d. 
Q, p, q, A, M, N є R
k є N, k>1
1) 
2) 
3) 
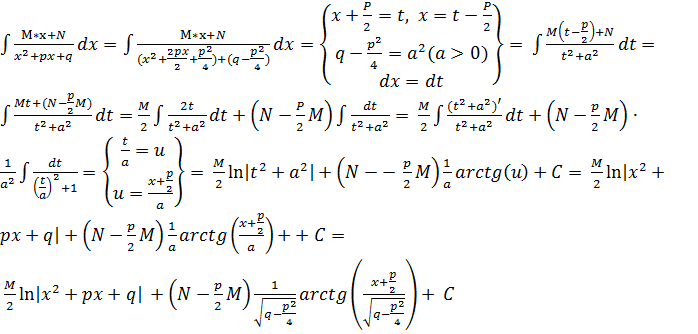
4) 
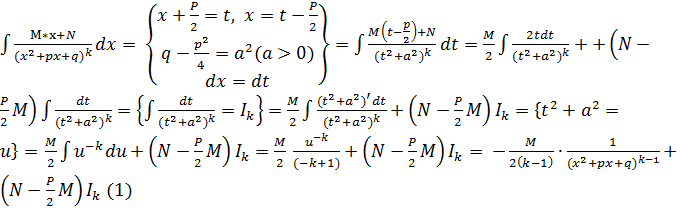
Ik =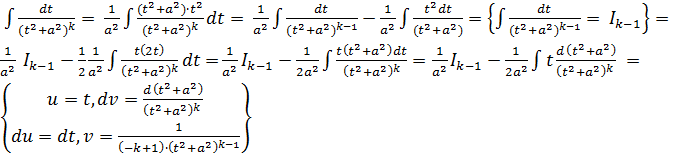 
Ik = 
Застосувавши рекурентну формулу (2) певне число раз, зведемо обчислення інтегралу Ik до обчислення інтегралу I1.
I1 = 
його обчислення дорівнює випадку 3
В результаті треба повернутися від t до x.
Інтегрування раціональних дробів
Загальний випадок
Раціональним дробом називається вираз вигляду 
, де 
і 
– многочлени степеня m i n відповідно.
Раціональний дріб (1) називається правильним, якщо m<n, і неправильним якщо m≥n
Зауваження: будь-який неправильний дріб можна подати у вигляді суми многочлена і правильного дробу.
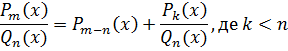
Приклад. 
(використовується ділення в стовпчик)
В курсі алгебри доводиться наступна теорема:
Нехай знаменник правильного раціонального дробу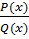 
можна подати у вигляді
(2)
Де 
Тоді для функції 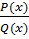має місце подання
(3)
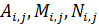– невизначені коефіцієнти.
Для того, щоб знайти ці коефіцієнти застосуємо метод невизначених коефіцієнтів та метод викреслення.
Метод невизначених коефіцієнтів
Згідно з цим методом сума дробів в правій частині рівності приводиться до спільного знаменника і одержаний в результаті цього чисельник порівнюваний з функцією P(x) тобто чисельником даного дробу
Приклад. 
x3: 2 = A + M A=1
x2: 1 = B – 2M + N M=1
x1: 1= B + M – 2N N=1
x0: 2= -A + B + N B=2
Таким чином ми отримали:
=> 
= 
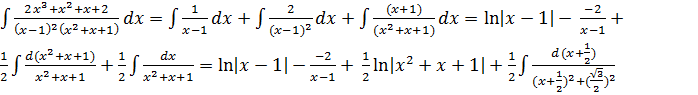
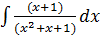Відповідь: 
2) Метод викреслення
Цей метод доцільно використовувати лише тоді, коли знаменник дробу має прості дійсні корені, коли має місце:
(4)
Ai є R
Знайдемо коефіцієнти Ai. Помножимо обидві частини рівності на (x-ai)
Ця рівність має місце для будь-яких х, в тому числи x=ai, покладемо x=ai і в результаті отримаємо
Таким чином, щоб знайти коефіцієнти 
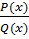в знаменнику дробу треба викреслити дужку з виразом (x-ai) і у виразі, що залишився покласти x=ai
Приклад 2.
Виходить: 
Метод Остроградського
Зауваження: як випливає з попередніх розділів (I-III) інтеграл від раціональної функції завжди можна обчислити і він зводиться до суми 3-х функцій: логарифмічної, арктангенса, раціональної.
Метод Остроградського дозволяє алгебраїчним шляхом виділити раціональну частину інтегралу від раціональної функції.
Метод Остроградського доцільно використовувати коли знаменник раціонального дробу має кратні корені, тоді інтеграл цієї функції можна подати у вигляді
Q1(x) – найбільший спільний дільник многочленів Q(x) та Q’(x); Q2(x)= 
P1(x), P2(x) – многочлени з невизначеними коефіцієнтами, степені яких на одиницю менше, ніж їх знаменники.
Якщо знаменник Q(x) має наступний вигляд:
то 
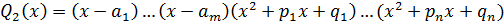
Продиференціюємо рівність (1)
Далі використати метод невизначених коефіцієнтів.
Приклад.
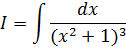
ð 
x5: 0=M
x4: 0=3A-4A+N
x3: 0=2B-4B+2M
x2: 0=C+3A-4C+2N
x1: 0=2B-4D+M
x0: 1=C+N
ІНТЕГРУВАННЯ ІРРАЦІОНАЛЬНИХ ВИРАЗІВ
У загальному випадку інтегрування ірраціональних функцій не можна звести до елементарних функцій, тобто їх не можна про інтегрувати у скінченному вигляді. Але у деяких випадках за допомогою метода підстановки вдається звести інтеграл від ірраціональної функції до інтеграла від деякої раціональної функції. Це означає, що даний інтеграл можна обчислити у скінченному вигляді.
Раціональні функції будемо позначати, як 
де 
- змінні, відносно яких дана функція є раціональною.
Приклад.
I. Інтегрування дробово-лінійної функції.
Нехай задано такі умови:
Зробимо заміну змінної:
де N = НСК(
), тоді з цього випливає, що:
З (1) випливає:
Таким чином, інтеграл від ірраціональної функції відносно x, ми звели до інтеграла від раціональної функції відносно змінної t. Як відомо інтеграл (2) завжди можна про інтегрувати в скінченному вигляді. Повернувшись до змінної x за допомогою підстановки 
одержимо необхідний результат, тобто інтеграл від змінної x.
Приклад.
Поділивши многочлен 
на многочлен 
з остачею, отримаємо:
Отже,
=
II. Інтегрування диференціальних біномів (біноміальних диференціалів).
Означення. Диференціальним біномом (біноміальним диференціалом) називається вираз вигляду:
де m, n, p Î Q, a, b Î R.
У загальному випадку, диференціальні біноми не можна про інтегрувати у скінченному вигляді. Але, за допомогою деяких підстановок, які називаються підстановками Чебишева, про інтегрувати диференціальний біном вдається.
1) Нехай
де m, n, p Î Q, a, b Î R. Крім того, нехай p Î Z. Тоді має місце така підстановка:
де r – НСК знаменників чисел m і n (тобто, якщо 
то r – НСК 
).
З цього випливає, що 
Тоді:
Отже, у такому випадку можна знайти у I у скінченному вигляді, а після цього повернутися до заміни, тобто: 
.
2) Нехай
де m, n, p Î Q, a, b Î R, крім того, 
Î Z. Тоді, нехай 
, де s – знаменник числа p (spÎ Z).
Тоді:
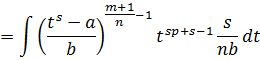
Так як Î Z, sp + s - 1Î Z, то:
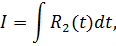
а отже I можна знайти у скінченному вигляді.
3) Нехай
де m, n, p Î Q, a, b Î R, крім того, 
Î Z. Тоді має місце така підстановка:
де s – знаменник числа p (spÎ Z).
Тоді:
так як 
Î Z, 
Î Z.
Зауваження. Доведено, що якщо жодне з 3-х чисел 
то інтеграл від диференціального бінома не можна виразити у скінченному вигляді.
Приклад.
отже застосуємо другу підстановку:
III. Інтегрування квадратичних ірраціональностей.
Нехай:
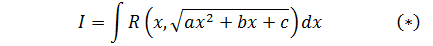
ОДЗ: 
.
1) Перша підстановка Ейлера.
Нехай D < 0.
Отже отримали, що 
і 
, тобто чисельник цього виразу не впливає на знак початкового виразу, тобто знак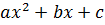 
співпадає зі знаком 
. Тоді, за умовою 
Підстановка: 
називається першою підстановкою Ейлера. Для визначеності, нехай: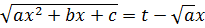 
. Звідси знайдемо х і dx:
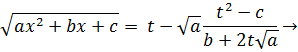
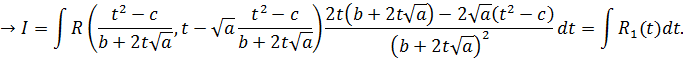
Отже, отримали раціональну функцію, яку можна про інтегрувати у скінченному вигляді.
2) Друга підстановка Ейлера.
Нехай D = 
> 0. Нехай 
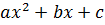корені тричлена . Тоді:
Здійснимо таку підстановку: 
Інтеграл вигляду (*) завжди можна про інтегрувати в скінченному вигляді, тобто подати у вигляді скінченної суми елементарних функцій.
Зауваження. Першу підстановку також можна зробити і для D > 0, при цьому розглядають 2 випадки:
1) a > 0. У такому випадку перша підстановка використовується в чистому вигляді.
2) a < 0, але c > 0. У цьому випадку, застосувавши підстановку 
, можна одержати інтеграл, що містить квадратичну ірраціональність, а, отже його можна про інтегрувати, за допомогою першої підстановки Ейлера.
ІНТЕГРУВАННЯ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ
1. Універсальна тригонометрична підстановка
Приклад:
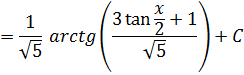
Зауваження. Універсальна підстановка часто приводить до складної раціональної функції.
2. Частинні підстановки
Розглянемо деякі властивості 
:
Властивість 1: Якщо 
, то 
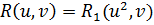(1)
Властивість 2: Якщо 
, то 
З рівності (1) випливає, що 
, тоді з властивості 1випливає, що має місце подання: 
Властивість 3: Якщо 
, то 
З властивості 1 випливає, що 
Таким чином .
1) Якщо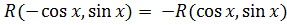 
, то
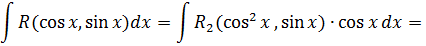
Підстановка 
2) Якщо 
, то
Підстановка 
3) Якщо 
, то
Підстановка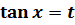 
Приклад:
