ПОНЯТТЯ РІВНОМІРНОЇ НЕПЕРЕРВНОСТІ ФУНКЦІЇ. ТЕОРЕМА КАНТОРА
Нехай функція y=f(x) визначена на замкнутому інтервалі [a, b]. Функція f(x) називається неперервною в точці х=х0, якщо:
1) 
=f(x0) (формальне означення).
Функція f(x) називається неперервною в точці х=х0, якщо:
2) ∀ε>0 ∃δ(ε)>0 ∀ x ∈ [a,b] |x-x0|< δ |f(x)-f(x0)|< ε (за Коші (на мові ´´ε – δ ´´).
3) ∀ {xn}->x0 (∀n ∈ N, xn ∈ [a,b] {f(x)}-> f(x0) (за Гейне (мова послідовностей)).
Функція f(x) називається неперервною на множині Х, якщо вона є неперервною у кожній точці цієї множини, тобто, якщо ∀ x ∈ X ∀ ε>0 ∃δ(ε,x)>0:
∀ x´ ∈ X, |x-x´|< δ: |f(x)-f(x´)|< ε.
Функція y=f(x) називається рівномірно неперервною на множині Х, якщо ∀ ε>0 ∃δ(ε): ∀ х, x ´ ∈ X |x- x ´|< δ: |f(x)- f(x ´)|< ε.
Відзначимо, що для рівномірної неперервності число δ одне для всіх точок x ∈ X (залежне від ε). А при «звичайній» неперервності у загальному випадку своє δ для кожного х. (Причому спільно δ не існує).
Приклад 1
y=f(x)=x2 X =[-l; l], l- const(l>0)
Доведемо, що ця функція буде рівномірно неперервною. Треба довести, що ∀ ε>0 ∃δ(ε)>0: ∀ x´, x´ ∈ [-l;l], |x´-x´´|< δ, |(x´)2 - (x´´)2|< ε.
Розглянемо останню нерівність:
|(x´)2-(x´´)2|=|x´-x´´|*|x´+x´´|<|x´-x´´|*||x´|+|x´´||< δ*2l= ε, де |x´ - x´´|< δ, |x´ + x´´|<2* δ.
Звідси маємо, що δ= 
Приклад 2
y=f(x) = x2 X = (-∞; +∞)
Побудова заперечення
1) ∀→∃
2) ∃→∀
3) <→≥
∃ ε>0: ∀ δ>0 ∃ x´, x´ ∈ (-∞; +∞), |x´-x´´|< δ |(x´)2-(x´´)2|≥ ε
x´= 
, x´´= + 
|x´-x´´|= 
< δ
|(x´)2-(x´´)2|=|x´-x´´|*|x´ + x´´|= 
≥1= ε
∃ ε=1: ∀δ>0, ∃ 
, + 
∈ (-∞; +∞), |x´ - x´´|< δ, |(x´)2-(x´´)2|≥ ε. Отже, ми довели, що на нескінченному проміжку функція є рівномірно неперервною.
Теорема Кантора
Означення
Якщо функція f(x) неперервна на сегменті [a;b], то вона рівномірно неперервна на цьому сегменті.
Доведення(від супротивного)
Нехай умова теоремі виконана, тобто f(x) неперервна на [a;b], але не рівномірно неперервна. Це означає, що треба довести, що ∀ε>0 ∃δ(ε)>0 ∃ x´, x´´ ∈ [a,b] |x´ - x´´|< δ |f(x´) - f(x´´)|≥ ε.
Візьмемо послідовність { δ n}→0 (∀ n ∈ N δ n>0) з додатних чисел, що збігається до 0.
(Наприклад, δ n= 
). ∀ δ n>0 xn´, xn´´ ∈ [a,b], |xn´-xn´´|< δn |f(xn´)-f(xn´´)|≥ ε (1) (Припущення, що (1) правильне).
Ми побудували дві послідовності: {xn´}, {xn´´}. Оскільки послідовність {xn´} складається з елементів сегмента [a, b], то вона є обмеженою і тому згідно з теоремою Больцано - Вейерштрасса з неї можна виділити збіжну послідовність {xnk´}.
Нехай 
=x0 (2), очевидно, що x0 ∈ [a,b].
Розглянемо |xnk´´-x0|=|(xnk´´ - xnk´)+(xnk´-x0)|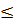 
|xnk´´ - xnk´|+|xnk´ - x0|→0, де |xnk´´- xnk´|, |xnk´-x0|→ 0 (при k→∞). Це означає, що 
→x0 (3). Оскільки за умовами теореми функція f(x) неперервна на сегменті [a,b], то вона буде тепер і в точці x0, що належить сегменту.
Згідно з означенням неперервності функції в точці за Гейне, одержимо, що
) = f(x0), 
) = f(x0). Звідси випливає, що |f(x´nk)-f(x´´nk)|→0(при k→∞)(4). Одержана умова (4) суперечить умові (1), якщо замість послідовності {xn} взяти {xnk}. Одержане протиріччя доводить теорему.
Означення
Коливанням функції f(x) на проміжку [a, b] називається ω=M-m, де M=sup x∈ [a,b] f(x), m=inf x∈ [a,b]f(x).
Наслідок з теореми Кантора
Нехай функція f(x) неперервна на проміжку [a,b]. Тоді ∀ε>0 ∃δ >0 таке що, якщо розбити проміжок [a, b] довільним чином на частинні проміжки з довжинами менше, ніж δ, то коливання функції f(x) на цих проміжках не перевищує ε.
Оскільки функція f(x)=x2 неперервна на [-l, +l], то за наслідком випливає, що вона рівномірна (суттєво, що проміжок замкнений). Контрприклад: y= 
, [0,1].
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
