Нехай функція f(x) визначена на проміжку [a,b] розіб’ємо цей проміжок точками xi на n частинних проміжків[xi-1, xi] при чому виконуються наступні нерівності:
a=x0<x1<x2<…<xn = b
Позначимо 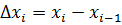 – довжина частинного проміжку [xi-1, xi]
– довжина частинного проміжку [xi-1, xi]
 – діаметр розбиття сегмента [a,b]
– діаметр розбиття сегмента [a,b]
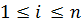
На кожному сегменті [xi-1, xi] візьмемо довільну точку εi , обчислимо значення функції в цій точці і складемо наступну суму:

Точки εi – називають проміжками на сегменті [xi-1, xi]
Сумі (1) називають інтегральною сумою (або сумою Рімана)
Сума (1) відповідає даному розбиттю сегмента і даному проміжних точок.
Означення. Число I називається границею інтегральних сум  при
при 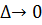 , якщо
, якщо  розбиття сегмента [a,b] з діаметром
розбиття сегмента [a,b] з діаметром  і
і  вибору проміжних точок частинами сегменту (
вибору проміжних точок частинами сегменту (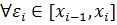 ) виконується нерівність
) виконується нерівність 
Якщо ця границя існує, то її називають визначеним інтегралом на проміжку [a,b] і позначають  , де a і b – відповідно нижня і верхня границя інтегрування; x – змінна інтегрування; f(x) – підінтегральна функція; f(x)dx – підінтегральний вираз
, де a і b – відповідно нижня і верхня границя інтегрування; x – змінна інтегрування; f(x) – підінтегральна функція; f(x)dx – підінтегральний вираз

Якщо визначений інтеграл існує, то функцію f(x) називають інтегрованою за Ріманом на проміжку [a,b].
Геометрична інтерпретація інтегральної суми та визначеного інтегралу
 неперервна і невід’ємна на [a,b]
неперервна і невід’ємна на [a,b]
Побудуємо графік цієї функції
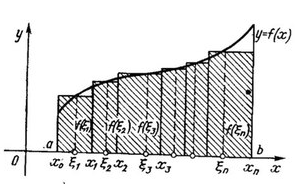
Означення. Криволінійною трапецією називають площу, обмежену графіком функції
y=f(x) віссю Ох і відрізками прямих x=a та x=b.
З геометричної точки зору інтегральна сума являє собою площу ступінчатої фігури, заштрихованої на нашому рисунку.
А визначений інтеграл площа криволінійної трапеції.
Будемо позначати розбиття сегмента [a,b] символом Т або Т[a,b]
Твердження 1. Якщо функція f(x)необмежена на [a,b], то вона не інтегрована на цьому сегменті.
Дійсно для будь-якого розбиття  хоча б на одному з часткових сегментів
хоча б на одному з часткових сегментів
[xi-1, xi] функція необмежена. А це означає, що за рахунок вибору проміжної точки εi часткову суму  можна зробити як завгодно великою(за модулем)
можна зробити як завгодно великою(за модулем)
А це означає, що множина інтегральних сум {  } є необмеженою. Звідси випливає, що не існує скінчена границя інтегральних сум, коли
} є необмеженою. Звідси випливає, що не існує скінчена границя інтегральних сум, коли 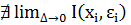 .
.
Твердження 2. Якщо функція f(x) обмежена на сегменті [a,b], то це ще не означає, що вона інтегрована на цьому сегменті.
Розглянемо приклад: функція Діріхле.

Очевидно, що ця функція є обмеженою на цьому проміжку, покажемо, що вона не інтегрована.
Розіб’ємо [a,b] на n часткових сегментів [xi-1, xi] і складемо дві інтегральні суми.

де всі  - раціональні числа
- раціональні числа
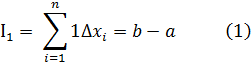
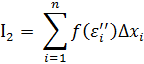
де всі  - ірраціональні числа
- ірраціональні числа

З (1), (2) випливає, що 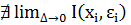
СУМИ ДАРБУ
Нехай функція f(x) визначена на проміжку [a,b]. Розіб’ємо цей проміжок на n частинних проміжків [xi-1, xi].
Введемо позначення: 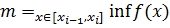 ,
, 
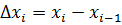
Введемо дві суми:
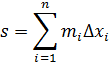

Ці суми називаються нижніми і верхніми сумами Дарбу, що відповідають даному розбиттю сегмента [a,b].
Твердження 3. Нехай  , s, S – нижня і верхня суми Дарбу, що відповідають даному розбиттю [a,b], тоді для будь-якого вибору проміжних точок εi виконується нерівність
, s, S – нижня і верхня суми Дарбу, що відповідають даному розбиттю [a,b], тоді для будь-якого вибору проміжних точок εi виконується нерівність 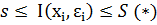
Якщо задане розбиття сегмента [a,b] на n [xi-1, xi], то виконується нерівність
 (
( вибору εi)
вибору εi)
Отже,  (i=1,2,…,n)
(i=1,2,…,n)
Просумуємо ці нерівності:

Отже, виконується нерівність (*), що і треба було довести.
Відзначимо, що нижню і верхню суму Дарбу можна подати у вигляді
 ,
,

(для даного розбиття [a,b])




