1. Составить уравнения прямой, образованной пересечением плоскости 3x-y-7z+9=0 с плоскостью, проходящей через ось Ох и точку Е(3;2;-5). (Ответ: 
)
2. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей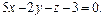 
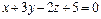параллельно вектору 
(Ответ: 
)
3. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 
перпендикулярно плоскости 
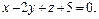(Ответ: 
)
4. Написать уравнение плоскости, которая принадлежит пучку плоскостей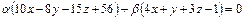 
и отстоит от точки С(3;-2;-3) на расстояние d=7.
(Ответ: 
)
5. Составить уравнения плоскостей, проектирующих прямую 
на координатные плоскости.
(Ответ: 
)
6. Составить уравнения прекции прямой 
на плоскость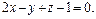 
(Ответ: 
)
7. Составить канонические и параметрические уравнения прямой, проходящей через точку М(2;0;-3) параллельно: 1) вектору 
2) прямой 
3) оси Ох.
(Ответ: 1)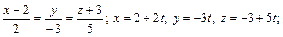 
2) 
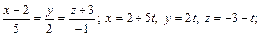
3) 
)
8. Даны вершины треугольника А(3;6;-7), В(-5;2;3) и С(4;-7;-2). Составить параметрические уравнения его медианы, проведенной из вершины С. (Ответ: 
)
9. Даны вершины треугольника А(3;-1;-1), В(1;2;-7) и С(-5;14;-3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине С. (Ответ: 
)
10. Составить канонические уравнения прямой, проходящей через точку М(2;3;-5) параллельно прямой: 
(Ответ: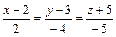 
)
11. Доказать параллельность прямых:
1) 
и 
2) 
и 
3) 
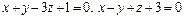и 
12. Доказать перпендикулярность прямых:
1) 
и 
2) 
и 
3) 
и 
13. Найти острый угол между прямыми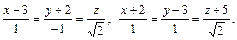 
(Ответ: 60о)
14. Составить уравнения прямой, которая проходит через точку
М1(-4;-5;3) и пересекает две прямые:
, 
. (Ответ: 
)
Прямая и плоскость
Задача. Найти точку пересечения прямой и плоскости:
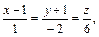
Решение. Запишем параметрические уравнения прямой: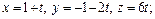 
подставим эти значения координат в уравнение плоскости: 
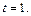Подставляя 
в параметрические уравнения, получим координаты точки пересечения: 
Ответ: М(2;-3;6).
Задача. Найти проекцию точки Р(2;-1;3) на прямую
Решение. Через точку Р проведем плоскость 
, перпендикулярную прямой L; навправляющий вектор прямой 
будет являться нормалью плоскости. Используя уравнение (1) § 6, имеем:
Проекцией точки Р на прямую L, таким образом, является точка пересечения прямой и плоскости:
Точка О(3;-2;4) – искомая проекция.
Задача. Вычислить расстояние d от точки Р(2;3;-1) до прямой
.
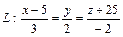Решение. Выберем на прямой L произвольную точку, например М(5;0;-25); будем считать, что направляющий вектор прямой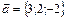 
приложен в точке М. Соединим точки М и Р и достроим фигуру до параллелограмма; его высота, проведенная из вершины Р, будет являться искомым расстоянием d: 
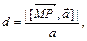где 
— длина векторного произведения, определяющая площадь параллелограмма, построенного на векторах 
и 
Вычислим координаты вектора : 
найдем векторное произведение 
:
определим его модуль:
длина вектора 
Найдем искомое расстояние: 
Ответ: 21.
Задача. Вычислить кратчайшее расстояние между двумя прямыми
и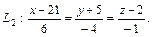 
Решение. Определим взаимное расположение прямых L1 и L2. Они непараллельны, т.к. неколлинеарны векторы 
и 
Проверим,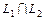 
или L1 и L2 скрещивающиеся; для этого выпишем 
найдем вектор 
и вычислим определитель из равенства (7) § 7:
L1 и L2 – скрещивающиеся.
Расстоянием d между скрещивающимися прямыми L1 и L2 будет являться высота параллелепипеда, построенного на векторах
т.е. 
Таким образом, 
