1. Даны две смежные вершины А(-3;-1) и В(2;2) параллелограмма ABCD и точка Q(3;0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма. (Ответ: 


 )
)
2. Найти проекцию точки Р(-6;4) на прямую 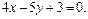
(Ответ: (-2; -1))
3. Найти точку М1, симметричную точке М2(8;-9) относительно прямой, проходящей через точки А(3;-4) и В(-1;-2). (Ответ: М1(10;-5))
4. Луч света направлен по прямой  Дойдя до прямой
Дойдя до прямой  луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. (Ответ:
луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. (Ответ:  )
)
5. Составить уравнения сторон треугольника, зная одну его вершину С(4;-1), а также уравнения высоты  и медианы
и медианы  , проведенных из одной вершины. (Ответ:
, проведенных из одной вершины. (Ответ: 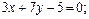
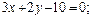
 )
)
6. Составить уравнения сторон треугольника, зная одну его вершину В(2;-7), а также уравнения высоты  и медианы
и медианы 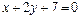 , проведенных из различных вершин. (Ответ:
, проведенных из различных вершин. (Ответ: 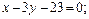

 )
)
7. Определить площадь треугольника, заключенного между осями координат и прямой  (Ответ: 9 кв. ед.)
(Ответ: 9 кв. ед.)
8. Составить уравнение прямой, которая проходит через точку Р(12;6) и отсекает от координатного угла треугольник с площадью, равной 150. (Ответ: 


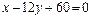 )
)
9. Через точку М(3;2) провести прямую так, чтобы ее отрезок, заключенный между осями координат, делился в данной точке пополам. (Ответ:  )
)
10. Даны уравнения двух сторон прямоугольника  и одна из его вершин А(-2;1). Вычислить площадь этого прямоугольника. (Ответ: 6 кв.ед.)
и одна из его вершин А(-2;1). Вычислить площадь этого прямоугольника. (Ответ: 6 кв.ед.)
11. Доказать, что прямая  пересекает отрезок, ограниченный точками А(-5;1) и В(3;7)
пересекает отрезок, ограниченный точками А(-5;1) и В(3;7)
12. Вычислить расстояние d между параллельными прямыми:  2)
2) 
(Ответ: 1) d=2,5; 2) d=0,5)
13. Точка А(5;-1) является вершиной квадрата, одна из сторон которого лежит на прямой  . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. (Ответ: 2 квадрата: 3х+4у-11=0, 4х-3у-23=0, 3х+4у-27=0; 3х+4у-11=0, 4х-3у-23=0, 3х+4у+5=0)
. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. (Ответ: 2 квадрата: 3х+4у-11=0, 4х-3у-23=0, 3х+4у-27=0; 3х+4у-11=0, 4х-3у-23=0, 3х+4у+5=0)
14. Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми: 1) x-3y+5=0, 3х-у-2=0; 2) x-2y-3=0, 2x+4y+7=0; 3) 3x+4y-1=0, 5x+12y-2=0. (Ответ: 1) 4х-4у+3=0, 2х+2у-7=0; 2) 4х+1=0, 8у+13=0; 3) 14х-8у-3=0, 64х+112у-23=0)
15. Составить уравнение биссектрисы угла между прямыми
х+2у-11=0 и 3х-6у-5=0, в котором лежит точка М(1;-3). (Ответ: 3х-19=0)
16. Составить уравнение биссектрисы острого угла, образованного двумя прямыми 3х+4х-5=0, 5х-12у+3=0. (Ответ: 7х+56у-40=0)
17. Через точку пересечения прямых 2х-5у-1=0 и х+4у-7=0 провести прямую, делящую отрезок между точками А(4;-3) и В(-1;2) в отношении  (Ответ: 2х-у-5=0)
(Ответ: 2х-у-5=0)
18. Найти уравнения прямых, принадлежащих пучку  и перпендикулярных к каждой из основных прямых пучка. (Ответ: 14х-7у+32=0; 7х+21у-75=0)
и перпендикулярных к каждой из основных прямых пучка. (Ответ: 14х-7у+32=0; 7х+21у-75=0)
Плоскость в пространстве
Уравнение  (1) определяет плоскость, проходящую через точку M0 (x0;y0;z0) и имеющую нормаль
(1) определяет плоскость, проходящую через точку M0 (x0;y0;z0) и имеющую нормаль 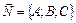 .
.
Уравнение (1) представим в виде:
 (2) где
(2) где 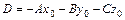 .
.
Уравнение (2) называется общим уравнением плоскости.
Уравнение плоскости, проходящей через точку M0(x0;y0;z0) параллельно векторам  и
и  :
:
 . (3)
. (3)
Уравнение плоскости, проходящей через точки M1 (x1;y1;z1) и M2 (x2;y2;z2) параллельно вектору  :
:
 (4)
(4)
Уравнение плоскости, проходящей через точки M1 (x1;y1;z1), M2 (x2;y2;z2) и M3 (x3;y3;z3):
 (5)
(5)
Уравнение плоскости «в отрезках»:
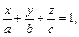 (6) где
(6) где  ― отрезки, отсекаемые плоскостью на координатных осях (считая от начала координат).
― отрезки, отсекаемые плоскостью на координатных осях (считая от начала координат).
Нормальным уравнением плоскости называется уравнение вида:
 (7)
(7)
где 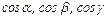 - направляющие косинусы нормали плоскости, р – расстояние от начала координат до плоскости.
- направляющие косинусы нормали плоскости, р – расстояние от начала координат до плоскости.
Общее уравнение плоскости приводится к нормальному виду (7) умножением на нормирующий множитель, определяемый формулой:
 (8)
(8)
знак нормирующего множителя берется противоположным знаку свободного члена D.
Отклонение  точки
точки  от плоскости дается формулой:
от плоскости дается формулой:
 (9)
(9)
или  (10)
(10)
Расстояние  от точки M* до плоскости:
от точки M* до плоскости:  , или
, или
 (11)
(11)
Угол между двумя плоскостями A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 определяется по формуле:
 ,
,
или  , (12)
, (12)
где  .
.
Условие параллельности двух плоскостей:
 (13)
(13)
Условие перпендикулярности двух плоскостей:
 (14)
(14)
Рассмотрим задачи.
Задача. Составить уравнение плоскости, которая проходит через точку М(2;-1;1) перпендикулярно к двум плоскостям 2x-z+1=0, y=0.
Решение. Т.к. искомая плоскость (обозначим ее через  ) проходит перпендикулярно двум данным плоскостям
) проходит перпендикулярно двум данным плоскостям 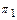 и
и  , то нормали этих плоскостей
, то нормали этих плоскостей 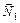 и
и  параллельны плоскости
параллельны плоскости  . Выпишем координаты
. Выпишем координаты 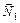 и
и  :
: 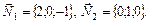
Составим уравнение плоскости  , используя (3):
, используя (3):



Задача. Вывести уравнение геометрического места точек, отклонение которых от плоскости 6x+3y+2z-10=0 равно –3.
Решение. Пусть  – точка искомого множества точек; по условию задачи:
– точка искомого множества точек; по условию задачи:

Получим:  – уравнение плоскости, параллельной данной.
– уравнение плоскости, параллельной данной.






