1. Определить, при каких значениях 
и 
следующие пары уравнений будут определять параллельные плоскости: 1) 2x+ly+3z-5=0, mx-6y-6z+2=0; 2) 3x-y+lz-9=0, 2x+my+2z-3=0;
(Ответ: 
)
2. Определить двугранные углы, образованные пересечением следующих пар плоскостей: 1) 
2) 
3) 
(Ответ: 1) 
и 
2) 
и 
3) 
)
3. Составить уравнение плоскости, которая проходит через точку М1(3;-2;-7) параллельно плоскости 
. (Ответ: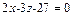 
)
4. Составить уравнение плоскости, которая проходит через две точки М1(1;-1;-2) и М2(3;1;1) перпендикулярно к плоскости 
. (Ответ: 
)
5. Определить, при каких значениях a и b плоскости 2x-y+3z-1=0, x+2y-z+b=0, x+ay-6z+10=0: 1) имеет одну общую точку; 2) проходят через одну прямую; 3) пересекаются по трем различным параллельным прямым. (Ответ: 1)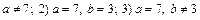 
)
6. Составить уравнение плоскости, которая проходит:
1) через точку М1(2;-3;3) параллельно плоскости Оху;
2) через ось Oz и точку М2(3;-4;7);
3) через точки Р1(2;-1;1) и Р2(3;1;2) параллельно оси Оу. (Ответ: 1) z-3=0; 2) 4x+3y=0; 3 ) x-z-1=0)
7. Вычислить площадь треугольника, который отсекает плоскость 5x-6y+3z+120=0 от координатного угла Оху. (Ответ: 240 кв. ед.)
8. Вычислить объем пирамиды, ограниченной плоскостью 2x-3y+6z-
-12=0 и координатными плоскостями. (Ответ: 8 куб. ед.)
9. Составить уравнение плоскости, которая проходит через точки М1(-1;4;-1), М2(-13;2;-10) и отсекает на осях абсцисс и аппликат отличные от нуля отрезки одинаковой длины.
(Ответ: 2x-21y+2z+88=0; 2x-3y-2z+12=0)
10. Вычислить расстояние между параллельными плоскостями:
1) x-2y-2z-12=0, x-2y-2z-6=0; 2) 2x-3y+6z-14=0, 4x-6y+12z+21=0;
3) 16x+12y-15z+50=0, 16x+12y-15z+25=0; 4 ) 2x-y+2z+9=0, 4x-2y+4z-21=0. (Ответ: 1) 2; 2) 3,5; 3) 1; 4) 6,5)
11. На оси Oz найти точку, равноудаленную от точки М(1;-2;0) и от плоскости 3x-2y+6z-9=0. (Ответ: 
)
12. Составить уравнения плоскостей, параллельных плоскости 2x-2y-z-3=0 и отстоящих от нее на расстояние d=5. (Ответ: 2x-2y-z-18=0; 2x-2y-z+12=0)
13. Составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей: 1) 4x-y-2z-3=0, 4x-y-
-2z-5=0; 2) 5x-3y+z+3=0, 10x-6y+2z+7=0. (Ответ: 1) 4x-y-2z-4=0;
2) 20x-12y+4z+13=0)
14. Составить уравнения плоскостей, которые делят пополам двугранные углы, образованные двумя пересекающимися плоскостями: 1) x-3y+2z-5=0, 3x-2y-z+3=0; 2) 5x-5y-2z-3=0, x+7y-2z+1=0).
(Ответ: 1) 4x-5y-z-2=0, 2x+y-3z+8=0; 2) x-3y-1=0, 3x+y-2z-1=0)
15. Составить уравнение плоскости, делящей пополам тот двугранный угол между двумя плоскостями 2x-y+2z-3=0, 3x+2y-6z-1=0, в котором лежит точка М(1;2;-3). (Ответ: 23x-y-4z-24=0)
Прямая в пространстве.
Прямая в пространстве задается несколькими способами.
1. Прямая как линия пересечения двух плоскостей:
(1)
при условии, что коэффициенты А1, В1, С1 непропорциональны коэффициентам А2, В2, С2.
Уравнение
(2)
называется уравнением пучка плоскостей.
2. Канонические уравнения прямой:
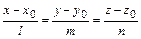, (3)
где точка М0(x0;y0;z0) — точка прямой; 
— направляющий вектор прямой.
3. Уравнения прямой, проходящей через две точки M1(x1;y1;z1) и M2(x2;y2;z2):
(4)
4. Параметрические уравнения прямой:
(5)
где t — произвольно изменяющийся параметр.
Угол 
между двумя прямыми
и 
равен углу между их направляющими векторами 
и 
, т.е. имеет место формула:
(6)
Условие, при котором прямые L1 и L2 лежат в одной плоскости:
(7)
Следовательно, прямые скрещиваются, если равенство (7) не имеет место.
Рассмотрим задачи.
Задача. Составить уравнение плоскости 
, проектирующей прямую 
на плоскость 
Решение. Искомая плоскость проходит через линию пересечения L перпендикулярно к плоскости 
. Составим уравнение пучка плоскостей:
Обозначим через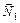 
и 
нормали плоскостей и соответственно. Тогда:
Найдем числа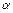 
и 
, учитывая, что 
т.е.
Пусть 
тогда 
Подставив эти значения в уравнение пучка, получим: 
Задача. Составить канонические и параметрические уравнения прямой
Решение. Чтобы перейти к каноническому и параметрическому заданиям прямой L зафиксируем на ней произвольную точку М0 и найдем ее направляющий вектор в виде: 
.
Пусть М0(х;у;0), тогда получим:
Т.е. 
Искомые уравнения: 
или 
Задача. Составить уравнения прямой L1, которая проходит через точку М1(-1;2;-3) перпендикулярно к вектору 
и пересекает прямую 
.
Решение. Канонические уравнения искомой прямой 
. Найдем ее направляющий вектор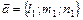 
; для этого решим систему, первое уравнение которой вытекает из перпендикулярности векторов 
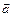и 
, а второе — из равенства (7):
Пусть 
Тогда 
Таким образом, 
