Приведем примеры решения типичных задач.
Задача. Проверить, что векторы, совпадающие с медианами любого треугольника, в свою очередь могут служить сторонами другого треугольника.
 Решение. Рассмотрим произвольный
Решение. Рассмотрим произвольный  . Пусть
. Пусть 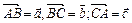 ; АМ, BN и СР – медианы
; АМ, BN и СР – медианы  . Выразим векторы
. Выразим векторы 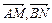 и
и  через векторы
через векторы  .
.
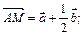
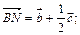
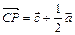 .
. 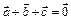 , так как векторы
, так как векторы  образуют замкнутую систему.
образуют замкнутую систему.
Вычислим сумму 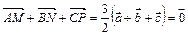 .
.
Таким образом, три вектора 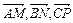 образуют замкнутую систему, то есть на медианах произвольного треугольника можно построить другой треугольник.
образуют замкнутую систему, то есть на медианах произвольного треугольника можно построить другой треугольник.
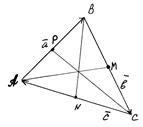
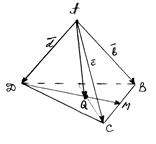
Задача. В тетраэдре 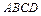 даны ребра, выходящие из вершины А:
даны ребра, выходящие из вершины А: 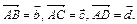 Выразить через эти векторы остальные ребра тетраэдра, медиану
Выразить через эти векторы остальные ребра тетраэдра, медиану  грани
грани 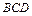 и вектор
и вектор  , где Q – центр тяжести грани BCD.
, где Q – центр тяжести грани BCD.
Решение. Ребра тетраэдра:

Медиана  :
:
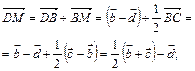
Для нахождения вектора  нужно учесть, что медианы точкой пересечения (центр тяжести треугольника) делятся в отношении 2:1. Таким образом,
нужно учесть, что медианы точкой пересечения (центр тяжести треугольника) делятся в отношении 2:1. Таким образом,
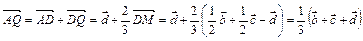 .
.
Задача. В параллелограмме ОАВС точки M и N – середины сторон  и
и 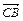 соответственно. Найти отношение
соответственно. Найти отношение 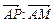 , где Р — точка пересечения
, где Р — точка пересечения 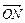 и
и 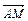 .
.
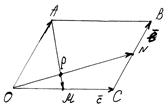 Решение. Пусть
Решение. Пусть 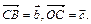 Тогда
Тогда 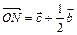 . Так как
. Так как 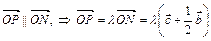 .
.
Из 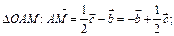
из 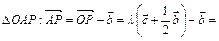

Так как 
То есть, 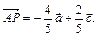 Таким образом,
Таким образом, 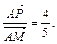
Задача. Разложить вектор 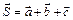 по трем некомпланарным векторам:
по трем некомпланарным векторам:

Решение. Если мы имеем три некомпланарных вектора, например 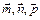 , то любой четвертый вектор
, то любой четвертый вектор 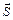 может быть однозначно разложен по векторам
может быть однозначно разложен по векторам 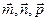 следующим образом:
следующим образом:
 . (3)
. (3)
То есть имеем:  .
.
Найдем числа  , одновременно не равные нулю. Для этого представим правую часть последнего равенства в виде:
, одновременно не равные нулю. Для этого представим правую часть последнего равенства в виде:
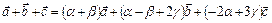 .
.
Получаем систему уравнений:

Подставляя эти значения в равенство (3), получим разложение вектора 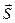 :
:
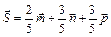 .
.
Задания для самостоятельного решения.
1. Каким условием должны быть связаны векторы 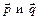 , чтобы вектор
, чтобы вектор 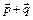 делил угол между ними пополам? Предполагается, что все три вектора отнесены к общему началу. (Ответ: p=q)
делил угол между ними пополам? Предполагается, что все три вектора отнесены к общему началу. (Ответ: p=q)
2. Зная векторы, служащие сторонами треугольника 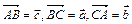 , найти векторы, соответственно коллинеарные биссектрисам углов этого треугольника.
, найти векторы, соответственно коллинеарные биссектрисам углов этого треугольника.
(Ответ: 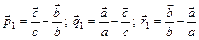 - внутренних углов;
- внутренних углов;
 - внешних углов)
- внешних углов)
3. На боковых сторонах АВ и ВС равнобедренного треугольника АВС расположены соответственно точки M и N так, что 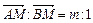 и
и 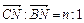 . Прямая MN пересекает высоту
. Прямая MN пересекает высоту 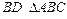 в точке О. Найти отношение
в точке О. Найти отношение  . (Ответ:
. (Ответ: 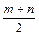 )
)
4. В  проведена биссектриса BD угла B. Найти разложение вектора
проведена биссектриса BD угла B. Найти разложение вектора  по векторам
по векторам 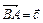 и
и 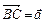 . (Ответ:
. (Ответ: 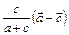 )
)
5. В правильном шестиугольнике 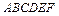 даны:
даны: 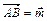 и
и  . Разложить по этим двум векторам
. Разложить по этим двум векторам 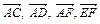 .
.
(Ответ: 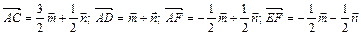 )
)
6. В равнобочной трапеции 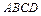 известно нижнее основание
известно нижнее основание  , боковая сторона
, боковая сторона 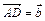 и угол между ними
и угол между ними 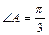 . Разложить по
. Разложить по 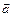 и
и  все векторы, составляющие остальные стороны и диагонали трапеции. (Ответ:
все векторы, составляющие остальные стороны и диагонали трапеции. (Ответ: 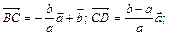
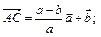
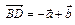 )
)
7. В 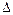 АВС сторона ВС разделена точкой D в отношении m:n, то есть
АВС сторона ВС разделена точкой D в отношении m:n, то есть 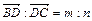 . Разложить вектор
. Разложить вектор 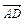 по векторам
по векторам 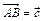 и
и 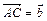 . (Ответ:
. (Ответ: 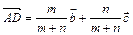 )
)
8. Точки K и L являются серединами сторон АВ и ВС параллелограмма ОАВС. Доказать, что точка пересечения диагоналей параллелограмма совпадает с точкой пересечения медиан 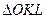 .
.
9. На сторонах АВ и АС треугольника АВС взяты соответственно точки M и N так, что 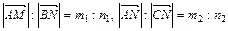 . Точку пересечения отрезков BN и CM обозначим через О. Найти отношения
. Точку пересечения отрезков BN и CM обозначим через О. Найти отношения 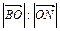 и
и 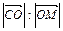 . Доказать, что при
. Доказать, что при 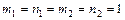 медианы
медианы  пересекаются в одной точке.
пересекаются в одной точке.
(Ответ:  )
)
10. Зная разложения векторов 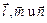 по трем некомпланарным векторам
по трем некомпланарным векторам 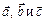 , проверить, будут ли
, проверить, будут ли 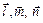 компланарны, и в случае утвердительного ответа дать линейную зависимость, их связывающую:
компланарны, и в случае утвердительного ответа дать линейную зависимость, их связывающую: 
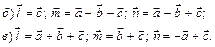
(Ответ:  - некомпланарны)
- некомпланарны)
11. Найти линейную зависимость между данными четырьмя неком-планарными векторами: 
(Ответ: 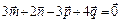 )
)
12. В разложении вектора 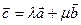 по двум неколлинеарным векторам
по двум неколлинеарным векторам 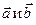 могут ли оба коэффициента разложения
могут ли оба коэффициента разложения 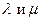 или один из них равняться нулю? (Ответ: а)
или один из них равняться нулю? (Ответ: а) 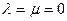 , если
, если 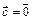 ; б)
; б) 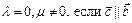 ; в)
; в) 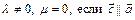 )
)






