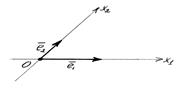
Аффинная (декартова) система координат на плоскости задается точкой О (начало координат) и парой приложенных к ней неколлинеарных (т.е. линейно неза-висимых) векторов 
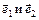. Векторы 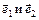называются базисными векторами (также говорят, что 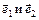образуют базис). Векторы 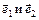определяют две
Рис. 4. координатные оси Ох1 и Ох2 и являются единичными векторами этих осей (рис. 4).
Система координат обозначается через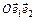 
или через Ох1х2.
Пусть М – какая-нибудь точка плоскости; обозначим через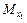 
и 
проекции точки М соответственно на оси координат Ох1 и Ох2 (рис.5). Длины векторов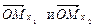 
называются соответственно первой и второй координатой точки М.
 |
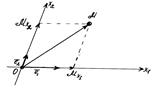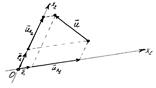
Рис.5. Рис.6.
Любая пара чисел х1, х2 однозначно определяет точку М; точка М с координатами х1, х2 обозначается так: М(х1, х2 ).
Координаты произвольного вектора 
относительно базиса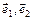 
(относительно базисных векторов 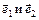) называются координатами вектора 
относительно системы координат 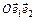; они являются проекциями вектора на оси координат и не зависят от выбора начала координат (рис. 6). Вектор с координатами х1, х2 обозначается так: 
; тогда
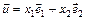. (1)
Координаты любой точки М в данной системе координат – это координаты вектора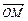 
в этой системе координат ( 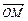называют радиус-вектором точки М).
Два вектора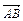 
и 
равны тогда и только тогда, когда равны их соответствующие координаты.
Если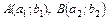 
, то для координат х1, х2 вектора 
имеем
.
Афинная система координат в пространстве строится аналогично с очевидными изменениями.
Задание прямоугольной системы координат на плоскости или в пространстве прежде всего предполагает выбор одной определенной единицы длины (масштаба). После того, как масштаб выбран, прямоугольная система координат определяется (как частный случай аффинной системы) требованием, чтобы единичные координатные векторы (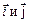
на плоскости; 
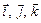в пространстве) были взаимно перпендикулярными ортами (векторы 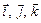называются основными или базисными ортами прямоугольной системы координат).
Любой вектор может быть разложен по базисным ортам 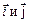на плоскости ( 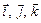в пространстве) следующим образом:
. (2)
Векторы 
называются компонентами вектора по осям координат.
Коэффициенты разложения x, y, z являются проекциями вектора на соответствующие оси координат.
Проекции 
вектора на три оси координат называются координатами вектора. Обозначение: = 
.
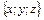Длина вектора вычисляется по формуле:
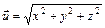. (3)
Направление вектора определяют его направляющие косинусы:
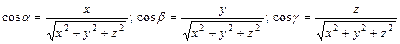(4)
где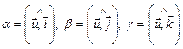 
.
Очевидно, что 
. (5)
Таким образом, 
. (6)
Если дано несколько векторов своими координатами:
,
то координаты суммы этих векторов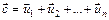 
равны суммам одноименных координат слагаемых векторов, т.е.
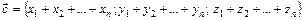. (7)
Координаты разности двух векторов равны разностям одноименных координат этих векторов, т.е. если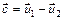 
, то
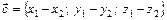. (8)
Координаты произведения вектора 
на скаляр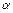 
равны произведениям координат вектора на тот же скаляр:
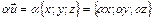. (9)
Условие коллинеарности двух векторов:
. (10)
Если даны две точки 
, то координаты точки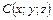 
, делящей вектор в отношении 
, т.е. 
, опреде-ляются так:
. (11)
