1. Даны  . Вычислить
. Вычислить  . (Ответ: 16)
. (Ответ: 16)
2. Векторы 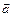 и
и  взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что  вычислить: 1)
вычислить: 1)  2)
2)  . (Ответ: 1) 24; 2) 60)
. (Ответ: 1) 24; 2) 60)
3. Какому условию должны удовлетворять векторы  , чтобы векторы
, чтобы векторы  и
и  были коллинеарны? (Ответ:
были коллинеарны? (Ответ:  )
)
4. Вычислить площадь параллелограмма, построенного на векторах 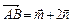 и
и  , где
, где 
 и
и  (Ответ: 37,5 кв.ед.)
(Ответ: 37,5 кв.ед.)
5. Разложить вектор 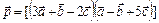 по взаимно перпендикулярным ортам
по взаимно перпендикулярным ортам 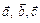 , образующим правую тройку. (Ответ:
, образующим правую тройку. (Ответ:  )
)
6. Зная векторы, совпадающие с двумя сторонами треугольника 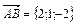 и
и  , вычислить площадь треугольника.
, вычислить площадь треугольника.
(Ответ: 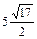 кв.ед.)
кв.ед.)
7. Даны вершины треугольника  и
и  . Вычислить длину его высоты, опущенной из вершины В на сторону АС. (Ответ: 5)
. Вычислить длину его высоты, опущенной из вершины В на сторону АС. (Ответ: 5)
8. Вычислить синус угла между диагоналями параллелограмма, построенного на данных векторах  и
и  .
.
(Ответ:  )
)
9. Вектор  , перпендикулярный к векторам
, перпендикулярный к векторам 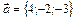 и
и  , образует с осью Оу тупой угол. Зная, что
, образует с осью Оу тупой угол. Зная, что  , найти его координаты. (Ответ:
, найти его координаты. (Ответ:  )
)
10. Вектор  , перпендикулярный к оси Oz и к вектору
, перпендикулярный к оси Oz и к вектору  , образует острый угол с осью Ох. Зная, что
, образует острый угол с осью Ох. Зная, что  , найти его координаты. (Ответ:
, найти его координаты. (Ответ:  )
)
11. Векторы  , образующие правую тройку, взаимно перпендикулярны. Зная, что
, образующие правую тройку, взаимно перпендикулярны. Зная, что  , вычислить
, вычислить 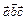 .
.
(Ответ: 24)
12. Вектор  перпендикулярен к векторам
перпендикулярен к векторам 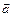 и
и  , угол между
, угол между 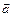 и
и  равен 30о. Зная, что
равен 30о. Зная, что  , вычислить
, вычислить 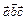 . (Ответ:
. (Ответ:  )
)
13. Доказать тождество 
14. Доказать, что векторы  , удовлетворяющие условию
, удовлетворяющие условию  , компланарны.
, компланарны.
15. Доказать, что точки А(1;2;-1), В(0;1;5), С(-1;2;1), D(2;1;3) лежат в одной плоскости.
16. Вычислить объем параллелепипеда, построенного на трех данных векторах 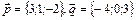 и
и  , и исследовать, образуют ли векторы левую или правую тройку. (Ответ:
, и исследовать, образуют ли векторы левую или правую тройку. (Ответ:  куб.ед., левая тройка)
куб.ед., левая тройка)
17. Объем тетраэдра 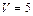 , три его вершины находятся в точках А(2;1;-1), В(3;0;1), С(2;-1;3). Найти координаты четвёртой вершины D, если известно, что она лежит на оси Оу. (Ответ:
, три его вершины находятся в точках А(2;1;-1), В(3;0;1), С(2;-1;3). Найти координаты четвёртой вершины D, если известно, что она лежит на оси Оу. (Ответ:  )
)
18. Найти вектор  , одновременно удовлетворяющий трем уравнениям:
, одновременно удовлетворяющий трем уравнениям: 
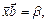
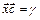 . (Ответ:
. (Ответ:  )
)
Прямая на плоскости
Уравнение вида  (1) называется уравнением прямой, проходящей через точку
(1) называется уравнением прямой, проходящей через точку  и имеющей нормаль
и имеющей нормаль  (нормаль или нормальный вектор — это вектор, перпендикулярный прямой).
(нормаль или нормальный вектор — это вектор, перпендикулярный прямой).
Уравнение (1) приводится к общему уравнению прямой:
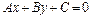 , (2)
, (2)
где  .
.
Уравнение прямой, проходящей через точку  и имеющей угловой коэффициент
и имеющей угловой коэффициент 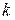 :
:
 , (3)
, (3)
где  (
(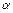 — угол наклона прямой к оси Ох).
— угол наклона прямой к оси Ох).
Уравнение прямой c угловым коэффициентом:
 (4)
(4)
где  — величина отрезка, который прямая отсекает на оси Оу, считая от начала координат.
— величина отрезка, который прямая отсекает на оси Оу, считая от начала координат.
Уравнение прямой, проходящей через две точки точки  и
и  :
:
 , (5)
, (5)
или
 , (6)
, (6)
где 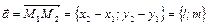 — направляющий вектор прямой; (6) – каноническое уравнение прямой.
— направляющий вектор прямой; (6) – каноническое уравнение прямой.
Угловой коэффициент прямой (5) вычисляется по формуле:
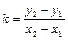 . (7)
. (7)
Один из углов между двумя прямыми вычисляется по формуле:
 , (8)
, (8)
где  и
и 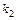 — угловые коэффициенты прямых.
— угловые коэффициенты прямых.
Условие параллельности двух прямых:
 . (9)
. (9)
Условие перпендикулярности прямых:
 , или
, или  . (10)
. (10)
Если ни один из коэффициентов уравнения (2) не равен нулю, то его можно преобразовать к виду:
 , (11)
, (11)
где  — величины отрезков, отсекаемых прямой на координатных осях Ох и Оу соответственно. Уравнение (11) называется уравнением прямой в «отрезках».
— величины отрезков, отсекаемых прямой на координатных осях Ох и Оу соответственно. Уравнение (11) называется уравнением прямой в «отрезках».
Нормальное уравнение прямой имеет вид:
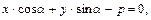 (12)
(12)
где p — длина нормали, опущенной из начала координат на данную прямую; 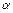 — угол между нормалью и осью Ох.
— угол между нормалью и осью Ох.
Уравнение (2) можно привести к уравнению (12); для этого его нужно умножить на нормирующий множитель  :
:
 (13)
(13)
Знак нормирующего множителя выбирается противоположным знаку свободного члена С уравнения (2).
Пусть дана какая-нибудь прямая l и произвольная точка 
 ― расстояние от точки
― расстояние от точки  до прямой l. Отклонением
до прямой l. Отклонением  точки
точки  от прямой l называется число
от прямой l называется число  , если точка
, если точка  и начало координат лежат по разные стороны от прямой l, и
и начало координат лежат по разные стороны от прямой l, и  , если
, если  и начало координат расположены по одну сторону от прямой l (если
и начало координат расположены по одну сторону от прямой l (если  , то
, то  ). Отклонение
). Отклонение  вычисляется по формуле:
вычисляется по формуле:
 (14)
(14)
или
 . (15)
. (15)
Чтобы найти расстояние d от точки до прямой, нужно вычислить отклонение и взять его модуль:  , т.е.
, т.е.
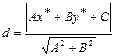 . (16)
. (16)
Совокупность прямых, проходящих через некоторую точку S, называется пучком прямых с центром S.
Если  и
и  - уравнения двух прямых, пересекающихся в точке S, то уравнение
- уравнения двух прямых, пересекающихся в точке S, то уравнение
 (17)
(17)
где  ― любые числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S. Уравнение (17) ― уравнение пучка прямых (с центром в точке S).
― любые числа, не равные одновременно нулю, определяет прямую, также проходящую через точку S. Уравнение (17) ― уравнение пучка прямых (с центром в точке S).
Рассмотрим задачи.
Задача. Точка E(1;-1) является центром квадрата, одна из сторон которого лежит на прямой 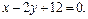 Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
Решение. Пусть сторона  . Диагонали AC и BD являются биссектрисами углов квадрата. Используя формулу (8), найдем угловой коэффициент одной из диагоналей:
. Диагонали AC и BD являются биссектрисами углов квадрата. Используя формулу (8), найдем угловой коэффициент одной из диагоналей:

 ;
;  ;
;  .
.
Зная 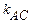 , точку
, точку  и применив (3), найдем уравнение диагонали АС:
и применив (3), найдем уравнение диагонали АС:  ;
; 
Решив систему уравнений прямых АВ и АС, найдем вершину А:

 т.е. А(-8;2).
т.е. А(-8;2).
Т.к.  , то, согласно (10),
, то, согласно (10), 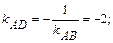 следовательно,
следовательно, 
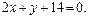
Точка Е является серединой АС. Используем формулу (11) из § 2  :
:
 .
.
Выражаем  :
:  ,
, 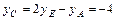 ; т.е. С(10;-4).
; т.е. С(10;-4).
 (опираясь на (9)); найдем уравнение DC:
(опираясь на (9)); найдем уравнение DC:
 ,
,  .
.
Аналогично, ВС:  ,
,  .
.
Ответ:  .
.
Задача. Составить уравнение сторон треугольника, зная одну его вершину В(2;6), а также уравнения высоты  и биссектрисы
и биссектрисы  , проведенных из одной вершины.
, проведенных из одной вершины.
 Решение. Координаты точки В не удовлетворяют уравнениям высоты и биссектрисы.
Решение. Координаты точки В не удовлетворяют уравнениям высоты и биссектрисы.
Пусть высота СН:  ,
,
биссектриса CD: 7x+y+5=0.
Найдем вершину C:
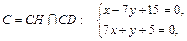
 т.е. С(-1;2).
т.е. С(-1;2).
Составим уравнение стороны ВС, используя формулу (5):
 ;
;
т.е. 
Из определения биссектрисы следует, что если на одной из сторон угла С дана точка В, то точка В*, симметричная точке В относительно биссектрисы CD этого угла, лежит на другой его стороне СА (см. рис.).
Таким образом, имеем:
1) 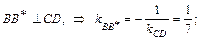


2) точка 
 т.е.
т.е. 
3) найдем точку В*: 
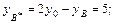
т.е. В*(-5;5).
Уравнение стороны СА: 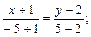

т.е. СА: 



Ответ: 
Задача. Составить уравнение прямой, которая проходит через точку Р(8;6) и отсекает от координатного угла треугольник с площадью, равной 12.
Решение. Запишем уравнение искомой прямой «в отрезках»:
 (11)
(11)
Если найдем значения параметров a и b, задача будет решена. Т.к. точка Р лежит на искомой прямой, ее координаты удовлетворяют уравнению (11):
 или
или 
Площадь треугольника, отсекаемого прямой от координатного угла, определяется формулой:  , т.к. отрезки a и b могут быть как одного, так и разных знаков. Согласно условию задачи, имеем:
, т.к. отрезки a и b могут быть как одного, так и разных знаков. Согласно условию задачи, имеем: 
Решим систему уравнений: 
Получим:  Таким образом, условию задачи удовлетворяют две прямые:
Таким образом, условию задачи удовлетворяют две прямые:  и
и 
Задача. Найти уравнение биссектрисы CD треугольника АВС, заданного координатами своих вершин: А(2;-1), В(-1;3), С(2;4).
Решение. Составим уравнения сторон АС и СВ:


Биссектриса – геометрическое место точек, равноудаленных от сторон угла. Пусть М(х;у) — каждая точка биссектрисы CD, тогда  или, применяя формулу (16), запишем:
или, применяя формулу (16), запишем:

Раскрывая модули, получим уравнения двух прямых:
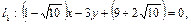

Одна из этих прямых является биссектрисой внутреннего угла, т.е. совпадает с CD, а другая – внешнего угла треугольника АВС.
Точки А и В должны находиться по разные стороны от прямой CD, т.е. отклонения 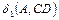 и
и  имеют разные знаки
имеют разные знаки  . Оценим знаки этих отклонений
. Оценим знаки этих отклонений  и
и  , используя формулу (15):
, используя формулу (15):

 ,
,
т.е. точки А и В лежат по одну сторону от прямой 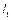 . Следовательно,
. Следовательно, 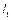 - биссектриса внешнего угла при вершине С.
- биссектриса внешнего угла при вершине С.
Ответ: 
Задача. Составить уравнение прямой, проходящей через точку пересечения прямых 
 и отсекающей на оси ординат отрезок
и отсекающей на оси ординат отрезок  Решить задачу, не определяя координат точки пересечения данных прямых.
Решить задачу, не определяя координат точки пересечения данных прямых.
Решение. Запишем уравнение пучка данных прямых:

 ,
,
т.е. 

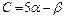 - координаты нормали прямой пучка. Т.к.
- координаты нормали прямой пучка. Т.к.  , то
, то  (по условию задачи),
(по условию задачи),
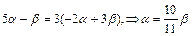 . Пусть
. Пусть  , тогда
, тогда  .
.
Подставляя в уравнение пучка, найдем уравнение искомой прямой:  .
.






