Наибольший общий делитель двух чисел и алгоритм Евклида.

Тема 1. Теория делимости

По свойству 2, Л-1 делимости целых чисел ( ) из делимости целого числа a на целое число b следует делимость на ± b. Поэтому при изучении вопроса о делимости целых чисел можно ограничиться лишь делимостью целых положительных чисел. В дальнейшем и будут рассматриваться лишь положительные делители чисел.

Определение 1. Любое целое число, которое делит одновременно числа a, b,..., l называется их общим делителем.

Определение 2. Наибольший из общих делителей чисел a, b,..., l называется наибольшим общим делителем этих чисел и обозначается символом
(a, b,..., l), НОД(a, b,..., l) или просто НОД.

Определение 3. Если (a, b,..., l) = 1, то числа a, b,..., l называются взаимно простыми.

Определение 4. Если каждое из чисел a, b,..., l является взаимно простым с каждым другим из них, то числа a, b,..., l называются попарно простыми.

Очевидно, что числа попарно простые всегда и взаимно простые. В случае двух чисел понятия ²попарно простые² и ²взаимно простые² совпадают.

П р и м е р ы.

Числа 6, 10, 15, из-за того, что (6, 10, 15) = 1 - взаимно простые.

Числа 8, 13, 21, из-за того, что (8, 13) = (8, 21) = (13, 21) = 1 - попарно простые.

Далее рассмотрим общие делители двух чисел.

Теорема 1. Если число a является кратным числа b, то совокупность общих делителей чисел a и b совпадает с совокупностью делителей одного числа b; в частности .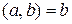

Д е й с т в и т е л ь н о, всякий общий делитель чисел a и b является делителем одного числа b. Обратно, если a является кратным b, то в соответствии со свойством 4, Л-1 ( [ b | а c | b c | a ]), каждый делитель числа b является также и делителем числа a, то есть является общим делителем чисел b и a.

Итак, множество общих делителей чисел a и b совпадает с множеством делителей числа b, а потому что наибольший делитель числа, b является само число b,то (a, b) = b.

Теорема 2. Когда числа a, b, q и r связанны соотношением

a = bq + r, (1)

то совокупность общих делителей чисел a и b совпадает с совокупностью общих делителей чисел b и r; в частности (a, b) = (b, r).

Д е й с т в и т е л ь н о, записанное равенство означает, что любой общий делитель чисел a и b в силу свойства делимости 8, Л-1 (если в равенства k + l + +... + + q +... + s относительно всех членов, кроме одного, известно, что они кратны b, то и этот один член кратен b), является делителем числа r, а каждый общий делитель чисел b и r по этому же свойству является делителем числа a.

Таким образом, множество общих делителей чисел a и b совпадает с множеством общих делителей чисел b и r и, итак, (a, b) = (b, r).

Перейдем теперь к нахождению наибольшего общего делителя двух чисел.

Еще Евклид[1] в книге VII своих ²Начал² предоставил способ нахождения НОД двух чисел, который известен теперь, как способ последовательного деления, или алгоритм Евклида.

Он состоит в следующем.

Пусть a и b - положительные целые (натуральные) числа и a > b. Если a не делится на b, то по теореме 1, Л-1 (какие бы ни были целые числа a и b, всегда существует единственная пара целых чисел q и r такая, что a = bq + r и 0 £ r < b)

a = bq + r ₁, 0 < r ₁< b.

Если b не делится на r ₁, то по этой же теореме

b = r ₁ q ₁ + r ₂, 0 < r ₂ < r ₁.

Если r ₁ не делится на r ₂, то

r ₁ = r ₂ q ₂ + r ₃, 0 < r ₃< r ₂

и т.д.

Этот процесс последовательного деления не может продолжаться бесконечно, так как в противном случае множество натуральных чисел b > r ₁> r ₂ >...> > >... не будет иметь наименьшего числа, а это противоречит принципу наименьшего числа (в ряде убывающих натуральных чисел меньших b не может содержаться больше чем b положительных). Итак, существует такое n, что делится на . Процесс последовательного деления заканчивается через шагов, и мы получаем систему равенств

a = bq ₀ + r ₁,

b = r ₁ q ₁ + r ₂,

............ (2)

r_{n -2} = r_{n -1} q_{n -1} + r_n,

r_{n -1} = r_nq_{n .}

Рассматривая эти равенства сверху вниз, на основе теоремы 2 получаем, что множество общих делителей чисел a и b совпадает с множеством общих делителей чисел b и r ₁, множество общих делителей чисел b и r ₁ совпадает с множеством общих делителей чисел r ₁ и r ₂, множество общих делителей чисел r ₁ и r ₂ совпадает с множеством общих делителей чисел r ₂ и r ₃ и т.д. В конце концов, можно прийти к заключению, что множество общих делителей чисел a и b совпадает с множеством общих делителей чисел r_{n -1} и r_n , и дальше, чем теорема 1 (если число a является кратным числа b, то совокупность общих делителей чисел a и b совпадает с совокупностью делителей одного числа b; в частности 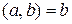) она совпадает с множеством делителей числа r_n. Тогда справедливые и соотношения _.

Итак, доказанная следующая теорема.

Теорема 3. НОД чисел a и b равняется последнему отличному от нуля остатку r_n в алгоритме Евклида.

С изложенного выше следует также справедливость такого утверждения

Теорема 4. Множество общих делителей чисел a и b совпадает с множеством делителей НОД этих чисел.

Из этой теоремы вытекает

Следствие. НОД чисел a и b делится на любой их общий делитель.

П р и м е р. Применим алгоритм Евклида для нахождения наибольшего общего делителя чисел 525 и 231.

Имеем,

525| 231

462 |2

231 | 63

189 |3

63| 42

42 | 1

42| 21

42 |2

Здесь положительный последний остаток есть r ₃= 21; поэтому (525, 231)= = 21.

Сформулируем теперь несколько теорем, связанных с понятием НОД двух чисел.

Теорема 5. Если натуральные числа a и b умножить на натуральное число m, то их НОД также умножится на число m, то есть.

(am, bm) = (a, b) m.

Д о к а з а т е л ь с т в о. Умножив обе части каждой из равенств (1) на число m, получаем равенства

am = bmq ₀ + r ₁ m,

bm = r ₁ mq ₁+ r₂m,

r ₁ m = r ₂ mq ₂+ r ₃ m,

...............

r_{n -2} m = r_{n -1} mq_{n -1} + r_nm,

r_{n -1} = r_nmq_n,

то есть мы имеем алгоритм Евклида для чисел am и bm. Поскольку последний отличный от нуля остаток здесь равняется r_nm, то (am, bm) = r_nm = (a, b) m.

Теорема 6. Если натуральные числа a и b разделить на любой их общий делитель , то НОД этих чисел также поделится на , то есть = .

Д е й с т в и т е л ь н о, = (a, b).

С другой стороны, по только что доказанной теореме 5

= .

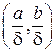
Итак, (a, b) = 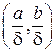. Отсюда = .

Из теорем 5 и 6 вытекают очевидные следствия:

Следствие 1. Частные 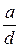и от деления чисел а и b на их наибольший общий делитель d взаимно простые, то есть = 1.

Следствие 2. Если частные 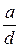и от деления чисел а и b на их общий делитель d взаимно простые, то d является их наибольшим общим делителем.

Следствие 3. Если (a, b) = 1, то (ac, b) = (c, b).

Д е й с т в и т е л ь н о, (ac, b) делит ac и bc (если (асс, b)делит b, то(ac, b)делити bc), значит число (ac, b), в силу теоремы 4(множество общих делителей чисел a и b совпадает с множеством НОД этих чисел), делит и число (ac, bc), которое равняется соответственно теореме 5 (если натуральные числа a и b у множить на натуральное число m, то их НОД также умножиться на число m) числу c, то есть делит с. Но (ac, b) делит и b, поэтому оно делит и (с, b). Обратно, (с, b) делит ac и b, поэтому оно делит и Таким образом, числа (асс, b) и (c, b) взаимно делят одно одного и, итак, они равные между собою.

Следствие 4. Если (a, b) = 1 и ac делится на b, то с делится на b.

Д е й с т в и т е л ь н о, соответственно теореме 1 (если число a является кратным b, то совокупность общих делителей чисел a и b совпадает с совокупностью делителей одного числа b), при ac, которое делится на b, имеем (ac, b) = b, и с следствия 3 (если (a, b) = 1, то (ac, b) = (c, b)) получаем b = (c, b), а этим (теорема 1) и приходится делимость c на b.

Следствие 5. Если число а является взаимно простым из каждым из чисел b и c, то а взаимно простое с произведением bc.

Приведем также утверждение, что характеризуют свойства НОД нескольких чисел.

Пусть а 1, а 2,..., an -1, аn - любые целые числа, среди которых хотя бы одно отлично от 0. Пусть (а 1, а 2) = d 2, (d 2, а 3) = d 3,..., (dn -2, аn -1)= dn -1, (dn -1, аn) = = dn. Тогда (а 1, а 2,..., аn) = (((× × × ((a 1, а 2), а 3),...), ). На основе этого факта можно дать другое определение наибольшего общего делителя.

Определения 2¢. Наибольшим общим делителем чисел а 1, а 2,..., аnназывают неотрицательный общий делитель этих чисел, которое делит любой другой их общий делитель.

Теорема 7. Если каждое a ₁, a ₂,..., a_m взаимно простое с каждым из чисел b ₁, b ₂,..., b_n, то и произведение a ₁× a ₂××× a_m взаимно простое с произведением b ₁× b ₂××× b_n.

Д е й с т в и т е л ь н о, соответственно следствию3 (Если (a, b) = 1, то )

(a ₁× a ₂××× a_m, b ₁) = (a ₂× a ₃××× a_m, b ₁) =... = (a_m, b ₁) = 1

и дальше, полагая ради краткости a ₁× a ₂××× a_m = A, точно таким же путем выводим

(b ₁× b ₂××× b_n, А) = (b ₂× b ₃××× b_n, А) = (b ₃× b ₄××× b_n, А) =... = (b_n, А) = 1.

Наименьшее общее кратное.

Определения 5. Целое число, которое делится на каждое из чисел a ₁, a ₂,..., a_n, называется общим кратным этих чисел.

Определения 6. Наименьшее из положительных общих кратных чисел a ₁, a ₂,..., a_n называется наименьшим общим кратным этих чисел и обозначается [ a ₁, a ₂,..., a_n ], или НОК(a ₁, a ₂,..., a) ли просто НОК.

Выясним процедуру определения наименьшего общего кратного (НОК) двух чисел.

Пусть (а, b) = d, a = da ₁, b = db ₁ и, тогда, в соответствии с следствием 1 теоремы 6 (частицы 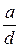и от деления чисел а и b на их наибольший общий делитель d взаимно простые) имеем (a ₁, b ₁) = 1. Пусть М - любое общее кратное чисел a и b. Так как М является кратным a, то М = ak, где k - целое. Но М является кратным и b, а это значит, что число

= =

должно быть целым и, соответственно, со следствием 4 теоремы 6 (если (a, b) = 1 и ac делится на b, то с делится на b) k должно делиться на b ₁. Итак, k = b ₁ t, где t - целое, причем для М выходит формула

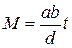. (3)

Обратно, очевидно, что М, которое представляется формулой (3) при любом целом t будет общим кратным a и b, и, таким образом, формула (3) дает общий вид всех общих кратных чисел a и b. Наименьшее положительное с этих общих кратных, то есть НОК, получаем при t = 1. Оно будет равняться

. (4)

Теперь формулу (3) можно записать следующим образом:

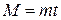. (5)

Формулы (5) и (4) приводят к теоремам:

Теорема 8. Совокупность общих кратных двух чисел совпадает с совокупностью кратных их общего наименьшего кратного.

Теорема 9. НСК двух чисел равняется их произведению, разделенному на их общий наибольший делитель.

Сформулируем также без доказательства свойства НOК нескольких чисел.

1) НОК чисел является делителем общего кратного этих чисел;

2) Пусть [ a 1, a 2] = m 2, [ m 2, a 3] = m 3,..., [ mn -2, an -1] = mn -1, [ mn -1, an ] = mn. Тогда [ ] = mn.

Приведенные свойства дают возможность свести вопрос нахождения НСК нескольких чисел к вопросу нахождения НОК двух чисел:

[ ] = [... [[ а ₁, а ₂], а ₃],..., a_n ].

Используется также другое определение наименьшего общего кратного.

Определения 6¢. Наименьшим общим кратным целых чисел называют неотрицательное общее кратное этих чисел, на которое делится любое их общее кратное.

[1] Евклид - древне-греческий математик. Работал в Александрии в 3 ст. до н. э. Главный трактат ²Начала² (15 книг), в котором содержатся основы аналитической геометрии, теории чисел, общей теории отношений и способы определения площадей и объемов.