Транспортная задача может быть решена непосредственно на транспортной сети. Для этого должны быть заданы: сеть путей в которой вершинами являются транспортные пункты (станции, пристани, предприятия и т.п.), а дугами - участки путей сообщения их соединяющие; количественное распределение отправления и прибытия однородного груза; значение показателя оптимальности сij для каждого участка. Если решается задача с ограничениями пропускной способности, то для некоторых участков должна быть указана пропускная способность dij.
Рассмотрим транспортную сеть на рис.. Сеть состоит из семи вершин (станций) и восьми дуг (перегонов между станциями). Возле вершин в скобках указываются размеры отправления и прибытия груза (соответственно со знаком + или -), если не указано ничего (см. вершина 7), то вершина транзитная. На каждом ребре указывается стоимость перевозки сij, а при необходимости через дробь пропускная способность участка dij (см. ребро 2-3). Соблюдение масштаба при построении сети необязательно.

3.2.1 Построение начального плана. При составлении начального плана перевозок необходимо добиться, чтобы весь груз из пунктов отправления был отправлен и все потребности пунктов назначения были покрыты. Специальных способов построения начального плана, близкого к оптимальному при решении задач на сети нет. При составлении начального плана нельзя допускать встречные перевозки. При наличии ограничений пропускной способности объем груза, провозимого по ребру не должен превышать его пропускной способности. Базисными ребрами называю ребра с незаполненной пропускной способностью по которым назначены перевозки. Базисные ребра должны составлять дерево: т.е. все вершины должны быть соединены и не должно быть замкнутых контуров. Вариант начального плана перевозок изображен на рис.

Число дуг, составляющих базис, должно быть n-1. В некоторых случаях, называемых случаями вырождения количество базисных дуг может быть меньше n-1. В этом случае начальный план представляет собой несколько изолированных деревьев (см. рис, а). Для того, чтобы довести количество базисных дуг до n-1 в базис можно ввести дуги с полностью заполненной пропускной способностью или незагруженные дуги, которые соединяют деревья. Если на дуге нет перевозки, то назначается нулевой поток. Направление этого потока произвольное (см. рис б, ребро 2.3).


3.2.2 Транспортная задача на сети без ограничений пропускной способности. Для решения транспортной задачи без ограничений пропускной способности методом потенциалов необходимо построить начальный план перевозок, а далее поэтапно улучшая, довести его до оптимального с помощью следующего алгоритма:
Шаг 1 - построение системы потенциалов. Одной из вершин присваивается любой потенциал (обычно присваивается достаточно большой потенциал, чтобы не иметь дело с отрицательными вершинами). Например v 1=100 (см. рис.).

Далее, продвигаясь по базисным дугам, рассчитываются потенциалы остальных вершин. При этом, если направление расчета совпадает с направлением следования грузопотоков, то к потенциалу предыдущей вершины прибавляется стоимость перевозки. При движении против потока стоимость перевозки из потенциала вычитается. Процесс производится до тех пор, пока не будут рассчитаны потенциалы всех вершин: v 7=100-30=70; v 6=70+35=105; v 5=105-40=65; v 4=65-30=35; v 3=35+25=60; v 2=60-20=40.
Шаг 2 - проверка оптимальности плана. План считается оптимальным если выполняются условия:
vj- ui £ cij; (1.8)
vj - ui = cij, если xij (1.9)
Возле небазисных ребер у которых не выполняется условие (1.8) не выполняется проставляется величина нарушения vj - ui - cij. В примере нарушение имеется на ребре 1.2 и составлет 35.
Шаг 3 - перераспределение грузопотоков. Выбираем дугу с наибольшим грузопотоком и находим замкнутый контур, состоящий из базисных дуг и выбранной дуги с нарушением (1-2-3-4-5-6-7-1). Продвигаясь по контуру в направлении от меньшего потенциала дуги к большему находим дугу с минимальным встречным грузопотоком (gmin=x56=15, см.рис.).

По ребру 1.2, вводимому в базис, пропускаем эту величину gmin. Продвигаясь по контуру, прибавляем величину gmin ко всем попутным потокам - вычитаем ее со всех встречных. После выполнения этой операции поток на ребре x56 стал равняться нулю. Данное ребро выводим из базиса и получаем новый план перевозок и переходим к шагу 1.
Полное решение примера см в.
Оптимальный план перевозок представлен на рис

Решение транспортной задачи на сети вручную удобно выполнять на одной схеме. При этом сама схема полигона, объемы груза в вершинах и стоимости перевозок наносятся чернилами, а грузопотоки и потенциалы карандашом. При корректировании плана изменяющиеся грузопотоки и потенциалы вытирают ластиком.
3.2.3 Транспортная задача на сети с ограничениями пропускной способности. Рассмотрим методику решения транспортной задачи на сети с ограничениями пропускной способности. На рис. изображена сеть с пятью вершинами и семью дугами. Пропускная способность дуг 2.5 и 1.4 ограничена и составляет соответственно 15 и 6 единиц. Начальный план перевозок включает 5-1=4 базисных дуги: 1.2, 2.4,1.3 и 4.5. Грузопоток также пропускается и по дуге 2-5, однако, так как на ней пропускная способность заполнена полностью, в базис эта дуга не включается. Алгоритм решения транспортной задачи с ограничением пропускной способности следующий:
Шаг 1 - присвоение потенциалов вершинам. Выполняется аналогично транспортной задаче без ограничений пропускной способности.
Шаг 2 - проверка оптимальности плана. План перевозок является оптимальным если выполняются следующие условия:
vj- ui £ cij, если xij=0 (1.10)
vj - ui = cij, если 0<xij<dij (1.11)
vj - ui ³ cij, если xi=dij (1.12)
Последнее условие также может быть представлено в следующем виде:
vj - ui = cij+dij, если xi=dij
Здесь dij - прокатная оценка. Экономический смысл прокатной оценки состоит в том, что она выражает дополнительный расход на единицу груза, перевозимого кружным путем из-за недостаточной пропускной способности. Поэтому при производстве мероприятий по увеличению пропускной способности в первую очередь необходимо обращать внимание на участки с наибольшей прокатной оценкой.
При обнаружении нарушений условий оптимальности возле соответствующих дуг записывается величина vj - ui - cij. При этом у незанятых дуг будут нарушения со знаком +, а у дуг с полностью заполненной пропускной способностью - со знаком “-”. В данном примере нарушения обнаружены на дугах 1.4 и 3.4, которые составляют соответственно 8 и 7.

Шаг 3 - перераспределение грузопотоков. Выбираем дугу с наибольшим по модулю нарушением. Находим замкнутый контур, состоящий из базисных дуг и дуги с нарушением. Если нарушение со знаком "+", то величина улучшения определяется минимальной перевозкой на встречных дугах или минимальной разностью между пропускной способностью и величиной перевозки на попутных.
xул=min[xвij, (dij - xij)п]
Полученная величина добавляется ко всем попутным и вычитается со всех встречных потоков.
Если нарушение со знаком "-", то величина улучшения определяется минимальной перевозкой на попутных дугах или минимальной разностью между пропускной способностью и величиной перевозки на встречных.
xул=min[xпij, (dij - xij)в]
Полученная величина добавляется ко всем встречным и вычитается со всех попутных потоков.
В примере максимальное нарушение +8 имеется на дуге 1.4. Находим замкнутый контур 1-4-2-1. Минимальный встречный поток x24=7, а дополнительный поток который можно пропустить по попутным дугам d14 - x14=6-0=6, таким образом:
xул=min(7, 6)=6.
В результате получаем новый план перевозок и переходим к шагу 1.
Полное решение примера см в.
Оптимальный план перевозок представлен на рис.

Приложение Б
ПРИМЕРЫ К ТРАНСПОРТНОЙ ЗАДАЧЕ НА СЕТИ
Б.1. Улучшение плана перевозок в задаче без ограничений пропускной способности.
Итерация 1. Начальный план С=3395.

Дуга 1.2 вводится в базис, а 5.6 исключается.
Итерация 2. С=2870.

Дуга 7.3 вводится в базис, а 2.3 исключается.
Итерация 3. Оптимальное решение С=2835.

Б.1. Улучшение плана перевозок в задаче с ограничениями пропускной способности.
Итерация 1. Начальный план С=318.
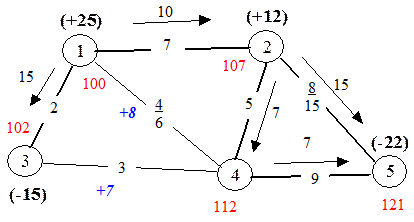
Назначаем поток на дуге 1.4 x14=6.
Итерация 2. Улучшений план С=270.
При перераспределении грузопотоков поток на этой дуге полностью заполнил пропускную способность, а на дуге 2.4 остался поток x24=1. Поэтому базис не изменился.

Дуга 3.4 вводится в базис, а 2.4 исключается.
Итерация 3. Улучшений план С=263.

Дуга 2.5 вводится в базис, а 1.2 исключается.
Итерация 4. Оптимальный план С=263.







