Әдебиеттер: [4]І тарау § 7, [5], [6] I тарау 5, [7] ІIІ-тарау.
Белгісіз кесінділерді белгілі кесінділер арқылы табу алгебралық формулалармен өрнектелетін теңдеулерге келтіріледі, яғни салу есебі формуламен өрнектелген кесінділерді салуға келтіріледі. Салу есебін бұлай шығару әдісі алгебралық әдіс деп аталады.
Алгебралық әдістің маңыздылығы — оның көмегімен салу есептерін циркуль және сызғышпен немесе басқа құралдармен шешуге болатындығында.
29-есеп. Төмендегі формулалармен берілген кесінділерді салу керек.
1) x=a+b-c (a+b>c)
2) x=na, мұндағы п — натурал сан;
3) х=  (мұндағы п — натурал сан);
(мұндағы п — натурал сан);
4) х=  (т және п — натурал сандар);
(т және п — натурал сандар);
5) х=  (егер b = а болса, онда х=
(егер b = а болса, онда х=  );
);
6) 
7) х= 
8) z= 
Көрсетілген кесінділерді салу мектеп курсында қарастырылады.
30-есеп.  кесіндісін салу керек, мұндағы а, b, с— берілген кесінділер.
кесіндісін салу керек, мұндағы а, b, с— берілген кесінділер.
Шешуі. Берілген өрнектің бір текті, бірінші өлшемді екенін атап өтейік. у =a+b және z=a-b делік. y және z кесінділерін (1-есеп, 1-салу), сонан соң х=  немесе
немесе  кесіндісін саламыз. Көбейткіштер ретінде бірінші өлшемді өрнектерді бірте-бірте жеке бөліп алсақ.
кесіндісін саламыз. Көбейткіштер ретінде бірінші өлшемді өрнектерді бірте-бірте жеке бөліп алсақ.
 ,
,  ,
,  болады, ең соңында болып
болады, ең соңында болып  шығады.
шығады.
Сөйтіп, есеп берілген үш кесіндіге пропорционал төртінші кесіндіні салуға келтіріледі (1-есеп, 5-салу).
31-есеп. Тең емес екі биіктігі бойынша тең бүйірлі үшбұрыш салу керек.
Шешуі. Талдау.  — іздеп отырған үшбұрышымыз, ВD= Һ b, АЕ= һ а оның биіктіктері болсын (38 а- сурет); егер үшбұрыштың бір қабырғасы белгілі болса, онда бұл үшбұрышты салуға болады. DС = х делік.
— іздеп отырған үшбұрышымыз, ВD= Һ b, АЕ= һ а оның биіктіктері болсын (38 а- сурет); егер үшбұрыштың бір қабырғасы белгілі болса, онда бұл үшбұрышты салуға болады. DС = х делік. 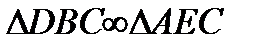 екендігі белгілі (сүйір бұрышы С ортақ тік бұрышты үшбұрыш болғандықтан). Үшбұрыштардың ұқсастығынан:
екендігі белгілі (сүйір бұрышы С ортақ тік бұрышты үшбұрыш болғандықтан). Үшбұрыштардың ұқсастығынан:
 (1)
(1)
 болғандықтан, (1) теңдіктен
болғандықтан, (1) теңдіктен 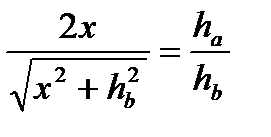 бұдан
бұдан 
Салу.  кесіндісін саламыз (38ә-сурет). (І-есеп, 3-салу).
кесіндісін саламыз (38ә-сурет). (І-есеп, 3-салу).  кесіндісін саламыз (І-есеп, 5-салу, (38б-сурет).
кесіндісін саламыз (І-есеп, 5-салу, (38б-сурет).
Ең соңында, іздеп отырған тең бүйірлі
АВС үшбұрышын
АС = 2х табаны және

биіктігі бойынша саламыз (38в-сурет).
Дәлелдеу. Салынған тең бүйірлі АВС үшбұрышында биіктіктер: ВD= ҺЬ, АЕ= һа екендігін дәлелдеу керек. Бірінші теңдіктің дұрыстығы анық, ал екіншісінің дұрыстығы анализ жасағанда келтірілген барлық формулалардың қайтарымдылығынан шығады.
Зерттеу. у=  кесіндісін, тек
кесіндісін, тек  немесе 2һь>һа болған жағдайда ғана салуға болады. Бұл шарт бойынша х кесіндісін салуға болады, олай болса іздеп отырған АВС үшбұрышын да салуға болады. Табандары мен биіктіктері тең теңбүйірлі екі үшбұрыш өз ара тең болатындықтан, есептің бір ғана шешімі болады.
немесе 2һь>һа болған жағдайда ғана салуға болады. Бұл шарт бойынша х кесіндісін салуға болады, олай болса іздеп отырған АВС үшбұрышын да салуға болады. Табандары мен биіктіктері тең теңбүйірлі екі үшбұрыш өз ара тең болатындықтан, есептің бір ғана шешімі болады.
Е с к е р т у. Есепті басқа тәсілмен оңай шешуге болады. Егер 0 нүктесі арқылы АЕ биіктігіне параллель және ВС қабырғасын Ғ нүктесінде қиып өтетін түзу жүргізсек, онда 0,5һа катеті мен һв гипотенузасы бойынша DҒВ үшбұрышын салуға болады. Бұл іздеп отырған үшбұрышымызды салу болып табылады.
 (мұндағы п — натурал сан);
(мұндағы п — натурал сан); (т және п — натурал сандар);
(т және п — натурал сандар); (егер b = а болса, онда х=
(егер b = а болса, онда х=  );
);


 кесіндісін салу керек, мұндағы а, b, с— берілген кесінділер.
кесіндісін салу керек, мұндағы а, b, с— берілген кесінділер. немесе
немесе  кесіндісін саламыз. Көбейткіштер ретінде бірінші өлшемді өрнектерді бірте-бірте жеке бөліп алсақ.
кесіндісін саламыз. Көбейткіштер ретінде бірінші өлшемді өрнектерді бірте-бірте жеке бөліп алсақ. ,
,  ,
,  болады, ең соңында болып
болады, ең соңында болып  шығады.
шығады. — іздеп отырған үшбұрышымыз, ВD= Һ b, АЕ= һ а оның биіктіктері болсын (38 а- сурет); егер үшбұрыштың бір қабырғасы белгілі болса, онда бұл үшбұрышты салуға болады. DС = х делік.
— іздеп отырған үшбұрышымыз, ВD= Һ b, АЕ= һ а оның биіктіктері болсын (38 а- сурет); егер үшбұрыштың бір қабырғасы белгілі болса, онда бұл үшбұрышты салуға болады. DС = х делік. 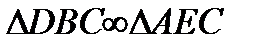 екендігі белгілі (сүйір бұрышы С ортақ тік бұрышты үшбұрыш болғандықтан). Үшбұрыштардың ұқсастығынан:
екендігі белгілі (сүйір бұрышы С ортақ тік бұрышты үшбұрыш болғандықтан). Үшбұрыштардың ұқсастығынан: (1)
(1) болғандықтан, (1) теңдіктен
болғандықтан, (1) теңдіктен 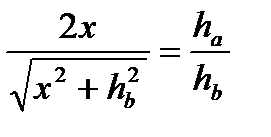 бұдан
бұдан 
 кесіндісін саламыз (38ә-сурет). (І-есеп, 3-салу).
кесіндісін саламыз (38ә-сурет). (І-есеп, 3-салу).  кесіндісін саламыз (І-есеп, 5-салу, (38б-сурет).
кесіндісін саламыз (І-есеп, 5-салу, (38б-сурет). биіктігі бойынша саламыз (38в-сурет).
биіктігі бойынша саламыз (38в-сурет).
 кесіндісін, тек
кесіндісін, тек  немесе 2һь>һа болған жағдайда ғана салуға болады. Бұл шарт бойынша х кесіндісін салуға болады, олай болса іздеп отырған АВС үшбұрышын да салуға болады. Табандары мен биіктіктері тең теңбүйірлі екі үшбұрыш өз ара тең болатындықтан, есептің бір ғана шешімі болады.
немесе 2һь>һа болған жағдайда ғана салуға болады. Бұл шарт бойынша х кесіндісін салуға болады, олай болса іздеп отырған АВС үшбұрышын да салуға болады. Табандары мен биіктіктері тең теңбүйірлі екі үшбұрыш өз ара тең болатындықтан, есептің бір ғана шешімі болады.





