16. Қабырғасы, оған іргелес бұрышы және өзге екі қабырғаларының қосындысы бойынша үшбұрыш салыңдар.
17. Катеті және гипотенузасы мен екінші катетінің қосындысы бойынша тік бұрышты үшбұрыш салыңдар.
18. Қабырғасы, оған іргелес бұрышы және өзге екі қабырғаларының айырмасы бойынша үшбұрыш салыңдар.
19. Қабырғасы, осы қабырғаға іргелес екі бұрышының айырмасы және өзге екі қабырғасының қосындысы бойынша үшбұрыш салыңдар.
Сабақ. НГО әдісі
Әдебиеттер: [4]§ 2, [5], [6] I тарау, 1.,2.,3., [7] 1-тарау
7-есеп. DАВС–ның ВС қабырғасында А және С төбелерінен бірдей қашықтықта жататын нүктені салыңдар. Есепті зерттеңдер.
Шешуі. Талдау. Кесіндінің ұштарынан бірдей қашықтықта болатын НГО кесіндіге орта перпендикуляр болады. Салу идеясы түсінікті.
Зерттеу. Есепте 3 жағдай болуы мүмкін (8-сурет):
1) Егер АВ=ВС болса, онда ∆АВС – тең бүйірлі және АС қабырғасына түсірілген перпендикуляр ВС қабырғасының В ұшы арқылы өтеді. Шешімі – В нүктесі.
2) Егер АВ<ВС болса, онда АС қабырғасына орта перпендикуляр ВС қабырғасын D нүктесінде қиып өтеді. Шешімі – D нүктесі.
3) Егер АВ>ВС болса, онда АС қабырғасына орта перпендикуляр ВС қабырғасын қиып өтпейді. Шешім жоқ.
| А |
| В |
| С |
| К |
| А |
| В |
| С |
| К |
| А |
| В |
| С |
| К |
| D |
8-есеп. Бұрыштың ішкі жағында А нүктесі берілген. А нүктесі арқылы өтетін және оның қабырғаларында тең кесінділер қиып өтетін түзуді салыңдар.
Шешуі.Талдау. Айталық, ізделінді түзу салынған және ОВ=ОС болсын (9-сурет). Тең бүйірлі ∆ОВС алдық. Егер биссектриса, медиана, биіктік О төбесінен жүргізілген болса, онда олар беттеседі. ОЕ биссектрисасы ВС табанына перпендикуляр немесе керісінше – ВС табаны ОЕ биссектрисасына перпендикуляр. Жоспары түсінікті болды және біз кері жүру арқылы салуды бастаймыз.
| А |
| О |
| В |
| С |
| Е |
9-сурет
Салу. О бұрышының биссектрисасын жүргіземіз. Одан кейін А нүктесі арқылы О бұрышының қабырғаларын В және С нүктелерінде қиып өтетін биссектрисаға перпендикуляр түзу жүргіземіз. Бұл кезде ОВ=ОС болады.
Дәлелдеу. ∆ОВС–да ОЕ биссектрисасы салу бойынша биіктік те болады. Сонда ∆ОВС тең бүйірлі болады: ОВ=ОС.
9 -е сеп. Бұрышының ішкі жағында жататын А нүктесі берілген. А нүктесінен өтетін түзуде жататын бұрыштың қабырғаларының арасындағы кесіндісі А нүктесімен қақ бөлінетіндей етіп түзу салыңдар.
Шешуі. Талдау. Есептің шартына сәйкес суретті саламыз (10-сурет). Айталық, ізделінді КС түзуі салынған болсын және СА=АК. А нүктесі КС қабырғасының ортасы болатын ∆ОКС алдық. А нүктесі арқылы бұрыштың қабырғасына параллель, екінші қабырғаны В нүктесінде қиып өтетін түзу жүргізейік. Одан кейін ОВ кесіндісін өлшеп ВК=ОВ салу керек. А және К нүктелері арқылы, басқа қабырғаны С нүктесінде қиып өтетін түзу жүргізіледі. Сол кезде СА=АК.
А
О
В
С
10-сурет К
Салуды және дәлелдеуді өз беттеріңше жүргізіңдер.
10-есеп. Шеңберден тыс жатқан А нүктесінен шеңберге жанамалар жүргізіңдер.
Тәсіл.
Шешуі.Талдау. Жанама – бұл түзу сызық; түзу салу үшін, екі нүкте болуы керек; оның біреуі А нүктесі берілген, шеңбердегі екінші нүктені, мысалға В, табу керек. Жанасу нүктесіне жүргізілген радиус, жанамаға перпендикуляр болады. Айталық ізделінді жанама салынған болсын (11-сурет).
| В1 |
| О |
| А |
| В |
| С |
11-сурет
ОА кесіндісін жүргіземіз. Тікбұрышты ∆ОАВ алдық. ОВ кесіндісін созып және оның созындысында ВС=ОВ салып көрелік. ∆ОАС-да АВ медиана және биіктік болады. Демек ∆ОАС тең бүйірлі. Олай болса ОА=АС. Тең бүйірлі ∆ОАС-ны үш қабырғасы бойынша: ОА=АС, ОС=2·R=2·ОВ салуға болады. ОС кесіндісі мен шеңбердің қиылысу нүктесі мен А нүктесін қосатын түзу шеңберге жанама болады.
Салу. 1) О және А нүктелерін кесіндімен қосамыз.
2) Үш қабырғасы бойынша ∆ОАС саламыз АС = ОА, ОС=2·R=2·ОВ.
3) ОС кесіндісі шеңберді В нүктесінде қиып өтеді.
4) А және В нүктелері арқылы ізделінді АВ жанамасын жүргіземіз.
Дәлелдеу. ∆ОАС – салу бойынша тең бүйірлі АС=ОА, бұнда салу бойынша ОВ=ВС. Сонда ∆ОАС-да АВ медиана болады. Бірақ тең бүйірлі үшбұрышта медиана сонымен бірге биіктік те, демек АВ 
ОС, АВ ОВ, АВ R. АВ шеңберге жанама болады.
Зерттеу. Есептің екі шешімі бар. Шеңберге екінші жанаманы жүргізу үшін, центрі А және радиусы АВ болатын шеңбер жүргізу керек. Бұл шеңбер берілген шеңберді В және В1 нүктелерінде қиып өтеді. А және В1 нүктелері арқылы берілген шеңберге екінші жанама өтеді.
| А |
| В |
| О |
| О1 |
| В1 |
12-сурет
Тәсіл.
Шешуі. Талдау. Айталық, ізделінді АВ жанамасы салынған болсын (12-сурет). Жанасу нүктесіне жүргізілген ОВ радиусы, жанасу нүктесіндегі жанамаға перпендикуляр екендігін еске түсіреміз. ∆ОАВ-да В бұрышы диаметрге тірелсе – онда ол тік бұрыш. О және А нүктелерін қосамыз; ОА кесіндісін О1 нүктесімен қақ бөлеміз; берілген шеңберді В және В1 нүктелерінде қиып өтетін, центрі О1 және радиусы О1А болатын шеңбер салу керек. АВ және АВ1 түзулері ізделінді жанамалар.
11-есеп. А және В екі елді мекендері түзу жолдың бір жағында орналасқан. Жолдың бойында С автобус аялдамасын АС+СВ ұзындықтарының қосындысы ең кіші болуы үшін қай жерде орналастыру керек?
| 13-сурет |
| А |
| С |
| В |
| В1 |
| О |
| a |
Шешуі. Талдау. Айталық түзудегі С нүктесі – ізделінді нүкте болсын (13-сурет), онда АС+СВ – ең қысқа қашықтық. АС сәулесін созып СВ=СВ1 салайық. а түзуі ВВ1 кесіндісінің орта перпендикуляры. Ізделінді С нүктесі АВ1 кесіндісі және а түзуінің қиылысуы болып табылады, сонымен бірге, АВ1=АС+СВ1 – түзу бойымен қашықтық ең қысқа болып табылады. Енді бұл есепті берілгенмен байланыстырып көрелік және В1 нүктесін а түзуінің басқа жағына СВ=СВ1 болатындай етіп көшіріп көрелік. В және В1 нүктелерін кесіндімен қосып, тең бүйірлі ∆СВВ1 (СВ=СВ1) аламыз. а түзуіне қарағанда симметриялы екендігін көрсетеді және СО кесіндісі тең бүйірлі ∆СВВ1-да биіктік, медиана, биссектриса болады.
12-есеп. Түзу және оның бір жағында жатқан А және В екі нүкте берілген. ∆АВС-ның периметрі ең кіші болатындай етіп, түзуде С нүктесін табу керек.
| 14-сурет |
| А |
| В |
| С |
| А1 |
| а |
| О |
Салу
1) А нүктесі үшін а түзуіне қарағандағы А1 симметриялы нүктені саламыз (14-сурет).
2) А1 және В нүктелерін кесіндімен қосып, оның а түзуімен қиылысуында С нүктесін аламыз.
3) А және С нүктелерін кесіндімен қосып, ізделінді ∆АВС үшбұрышын аламыз.
Дәлелдеу
Симметриялы нүктелердің анықтамасы бойынша АА1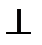 
а және АО=ОА1 (О – АА1 және а түзулерінің қиылысу нүктесі). Сонда анықтама бойынша ∆АСА1-да ОС кесіндісі биіктік және медиана болады. Сонда ∆АСА1– тең бүйірлі және анықтама бойынша А1С=АС. Салу бойынша А1В кесіндісі ең қысқа, сонымен бірге А1В=А1С+СВ=АС+СВ. ∆АВС Р=АС+СВ+АВ=А1В+АВ периметрі ең қысқа, ал С төбесі салу бойынша а түзуінде жатыр.
