[4] І тарау §2, [5], [6] I тарау, 1.,2.,3., [7] 1-тарау
2-есеп. Қабырғаларының орталары берілген болса, онда үшбұрышты салу керек.
Берілгені: D, N, K нүктелері - үшбұрыш қабырғаларының орталары.
Салу керегі: ∆АВС.
Шешуі.Талдау.
А К С
В
D
N
2 5
3 3
4 4
3-сурет
Салу. 1) Бізге берілген қабырғалардың орталарын D, N, К әріптерімен белгілейміз.
2) Оларды кесінділермен қосамыз. ∆DNК аламыз.
3) D нүктесі арқылы КN-ге параллель түзу; N нүктесі арқылы DК-ға параллель түзу; К нүктесі арқылы DN-ге параллель түзу жүргіземіз.
4) Жүргізілген түзулер А, В, С нүктелерінде қиылысады. ∆АВС – ізделінді.
Дәлелдеу. АС║DN-дегі сәйкес бұрыштар болғандықтан 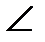 1 =
1 = 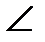 2 (салу бойынша). АС║DN-дегі айқыш бұрыштар болғандықтан
2 (салу бойынша). АС║DN-дегі айқыш бұрыштар болғандықтан 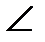 3 =
3 = 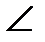 4. ВС║DК-дегі айқыш бұрыштар болғандықтан
4. ВС║DК-дегі айқыш бұрыштар болғандықтан  4 =
4 =  5 (салу бойынша). Осыдан
5 (салу бойынша). Осыдан  3 =
3 =  5. АВ║КN-дегі айқыш бұрыштар болғандықтан
5. АВ║КN-дегі айқыш бұрыштар болғандықтан 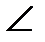 6 =
6 = 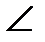 7 (салу бойынша). Сонда ∆АDК = ∆DNК (DК – ортақ қабырға,
7 (салу бойынша). Сонда ∆АDК = ∆DNК (DК – ортақ қабырға, 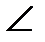 3 =
3 = 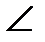 4,
4, 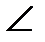 6 =
6 = 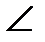 7)
7)  АК = DN. Енді ∆АDК = ∆ВDN (АК = DN,
АК = DN. Енді ∆АDК = ∆ВDN (АК = DN, 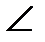 1 =
1 = 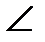 2,
2, 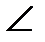 3 =
3 = 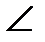 5)
5)  АD = DВ. Демек, D нүктесі – анықтама бойынша АВ кесіндісінің ортасы. N және К нүктелері ВС және АС кесінділерінің орталары екендігі осыған ұқсас дәлелденеді.
АD = DВ. Демек, D нүктесі – анықтама бойынша АВ кесіндісінің ортасы. N және К нүктелері ВС және АС кесінділерінің орталары екендігі осыған ұқсас дәлелденеді.
3-есеп. Екі қабырғасы және үшінші қабырғаға жүргізілген медиана бойынша үшбұрыш салу.
Берілгені: в, с, ma.
Салу керек: ∆АВС
Шешуі. Талдау. Айталық, ізделінді ∆АВС салынған болсын (4-сурет). АК медианасын жүргіземіз (ВК=КС). Демек егер АК медианасын екі есе ұзартса, онда үш қабырғасы бойынша ∆АЕС-ын салуға болады. Екі қабырғасы және олардың арасындағы бұрыш бойынша ∆КЕС=∆АВК. Тең үшбұрыштарда СЕ=АВ, ал басқа қабырғасы берілген. Одан кейін АЕ-де АК саламыз және К нүктесі арқылы СК сәулесін жүргіземіз де, онда КВ=СК саламыз. Жоспары түсінікті және салуға көшеміз.
| А |
| В |
| С |
| К |
| Е |
| 4-сурет |
Салу. 1) Үш қабырғасы бойынша ∆АЕС-ын (АЕ = 2 ma, AС = в, СЕ= с) саламыз.
2) АК = ma болатын К нүктесінен СК = КВ саламыз.
3) А және В нүктелерін қоссақ ізделінді ∆АВС аламыз.
Дәлелдеуі. Салуымыз бойынша AС = в, СЕ= с, АЕ = 2 ma. АК = ma= АЕ, СК=КВ. АКВ және ЕКС вертикаль бұрыштар. Демек ∆КЕС=∆АВК. Олай болса, СЕ=АВ=с. АВС үшбұрышы берілген шарттарды қанағаттандырады.
Зерттеу. Егер көмекші ∆АЕС-ын салу мүмкін болса, ∆АВС салуға болады. ∆АЕС-ын в+с >2 ma орындалғанда шешімі болады.
4-есеп. Үш медианасы бойынша үшбұрыш салу.
| 5-сурет |
| О |
| В |
| А В1 С |
| А1 |
| С1 |
| Е |
Шешуі. Талдау. Айталық, ізделінді ∆ АВС үшбұрышы салынған болсын (5-сурет). АА1, ВВ1, СС1 медианалары. Үшбұрыштың медианалары бір нүктеде қиылысады және онда төбесінен бастап санағанда 2:1 қатынаста бөлінеді. Әрбір медиананы 3 тең бөлікке бөліп және олардан ∆ОВ1Е құрасыру керек. Әрі қарай қимыл жоспары түсінікті.
Салу. 1. Берілген әрбір медиананы 3 тең бөлікке бөлеміз.
2. Әрбір медиананың үштен бір бөліктерінен 3 қабырғасы бойынша ∆ОВ1Е саламыз.
3. Одан кейін О және Е нүктелері арқылы түзу жүргіземіз және онда ОЕ кесіндісіне тең болатын ЕС және ОС1 кесінділерін саламыз.
4. С және В1 нүктелері арқылы түзу жүргіземіз де онда В1 нүктесінен В1С кесіндісіне тең АВ1 кесіндісін саламыз.
5. Әрі қарай А және С1 нүктелері арқылы түзу жүргіземіз және онда С1 нүктесінен АС1 кесіндісіне тең С1В кесіндісін саламыз.
6. В және С нүктелерін кесіндімен қосамыз.
7. Алынған ∆АВС ізделінді болады.
Дәлелдеуі. Салу бойынша ∆АВС-да АВ1=В1С және АС1= С1В, сондықтан ВВ1 және СС1 медианалар болып табылады, ал үшінші медиана олардың қиылысу нүктесі арқылы өтеді. Әрбір медиана салуы бойынша ∆ОВ1Е–ның сәйкес қабырғасынан 3 есе үлкен болады. Сондықтан ∆АВС ізделінді болады.
Зерттеу. Егер берілген медианалар үшбұрыш теңсіздігін қанағаттандырса, онда есептің жалғыз ғана шешімі бар.






