Сабақ. Параллелограм және тіктөртбұрыш салу

Әдебиеттер: [4] І тарау§ 2, [5], [6] I тарау, 1.,2.,3., [7] 1-тарау, [8] І тарау §2-7, § 4(1-2-мысал.), § 5 (1-мысал)., [10] І тарау § 1-7, § 2 (2-мысал), § 4 (1-2-мысал)

13-есеп. Табаны, оған жүргізілген биіктігі және диагоналдар арасындағы бұрышы бойынша параллелограмм сызыңдар.

Шешуі. Талдау. Есеп шешілген, яғни табаны АВ= а, бұл қабырғаға жүргізілген биіктігі ЕҒ=h, диагоналдар арасындағы бұл қабырғаға қарайтын бұрышы < А0В= 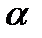болатын АВСD параллелограмм салынған болсын (15-а сурет).

Егер а =АВ салсақ параллелограмның екі төбесі салынады. Енді диоганалдарының қилысу нүктесі О салынса параллелограмм салынады. О нүкте екі шартқа бағынады. Ол AВ-дан һ/2 қашықтықта жату керек және АВ= а кесінді бұрышпен көрінетін нүктелер жиынына кіру керек. Сондықтан салу жұмысын былайша жүргіземіз (15-б сурет).

а)

б)

15-сурет

 

 

Салу: 1) Түзу бойынша АВ= а кесінді өлшеп саламыз.

2) АВ кесінді бұрышпен көрінетін нүктелер жиынын саламыз. Ол АВ мен бұрыш жасайтын АТ түзуіне А нүктеде жүргізілген перпендикуляр мен АВ-ның қақ ортасынан жүргізілген перпендикулярдың қиылысу нүктесі К центрі АК радиусы болатын шеңбер болады (6 ⁰ негізгі нүктелер жиыны).

3) АВ-ға ^ жүргізіп, оның бойына Һ кесіндіні өлшеп салып һ/2 болатын нүктеден d, h-тың ұшынан ℓ түзулерін АВ-ға параллель етіп жүргіземіз.

4) d-ның шеңбер мен қиылысу нүктелері О мен О₁ табамыз.

5) АО∩ℓ=С, ВО∩ℓ=D, ВО₁∩ℓ=D₁, AО₁∩ℓ=C₁ нүктелерді табамыз. Сонда АВСD, AВС₁D₁ іздеген параллелограмм болады.

Дәлелдеу. Салуымыз бойынша АВêêdççℓ болғандықтан АО=ОС, BО=ОD. Сондықтан АВСD параллелограмм болады және АВ мен d, d мен ℓ түзулер арасы һ/2-ге тең болғандықтан параллелограмм биіктігі һ-қа тең болады. Салу бойнша ÐА0В= 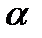тең. Демек АВСD есептің үш шартында қанағаттандырады. Дәл осы сияқты А¹В¹С¹D¹-де есептің үш шартын қанағаттандырады. Сондақтан олар іздеген параллелограмм болады.

Зерттеу. 1) салу әруақытта бір мәнді орындалады.

2) салу да АВ кесінді бұрышпен көрінетін нүктелер жиыны екі-симметриялы. Ұштары А мен В болатын доғалардан тұрады.

3) Салуда һ кесіндіні АВ мен анықталатын төменгі жарты жазықтықта өлшеп салуға болады.

4) Салуда екі нүкте О₁ мен О₂ шығуы бірғана нүкте шығуы (d түзу шеңберге жанама боған жағдайда) мүмкін және шеңбер мен d түзу қилыспауы мүмкін.

Сондықтан есептің шешуі екеу болуы, біреу болуы немесе тіпті болмауы мүмкін.

14-есеп. р периметрі мен диагональдарының қатынасы бойынша ромбы салу керек.

C

A

E

D

P

m

O2

O1

Q

n

n

B

16-сурет

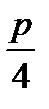Шешуі.Талдау. АВСВ іздеп отырған ромбы болсын (16-сурет). Ромбның қабырғасы АВ= олай болса, бұдан ромбының A мен В төбесін салуға болатындығы шығады. Бұл төбелер — белгілі АВ қабырғасының ұштары. Шарт бойынша АС: ВD = m:n (анық болуы үшін т>п делік) немесе 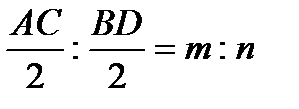яғни АЕ:ВЕ=т:п.

 

Көмекші АВЕ үшбұрышын қарастырайық. Егер бұл үшбұрыш салынатын болса, онда ромбыны салу оңай. АВЕ үшбұрышын салу Е төбесін салуға тәуелді. Е төбесі екі шартты қанағаттандыруы тиіс:

1) бұл нүктеден АВ кесіндісі тік бұрышпен көрінуі тиіс;

2) бұл нүктенің А және В төбелерінен қашықтықтарының қатынасы АЕ:В

Е=т:п тең болуы тиіс.

Салу. 1) кез келген түзудің бойынан А нүктесін алып, АВ= 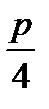болатын етіп, В нүктесін саламыз (16-суретті қараңыз).

2) 1-шартты қанағаттандыратын НГО саламыз; бұл — шеңбері болады.

3) 2-шартты қанағаттандыратын НГО саламыз; бұл Аполлоний шеңбері болады.

4) және шеңберлерінің қиылысу нүктелерінің бірі Е нүктесін белгілейік. АВЕ — үшбұрышы іздеп отырған үшбұрышымыз.

5) Ромбы салайық. Ол үшін АЕ қабырғасының созындысына АЕ=ЕС және ВЕ қабырғасының созындысына ВЕ=ЕD саламыз: АВСD — іздеп отырған рoмбымыз.

Дәлелдеу. АВЕ — іздеп отырған үшбұрышымыз. Бұл AB= 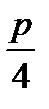салудан және екі н. г. о. қиылысу нүктесі ретінде, осы н. г. о. екеуінің де қасиетіне ие болатын Е нүктесінің қасиетінен шығады.

Салынған АВСD төртбұрышының диагональдарының қиылысу Е нүктесі оларды қақ бөлетіндіктен және бұл диагональдардың арасындағы бұрыш тік болғандықтан, бұл төртбұрыш іздеп отырған ромбымыз болады.

3ерттеу. Есепті шешу негізінде екі шеңбердің қиылысу нүктесі болатын Е нүктесін салу болатынын біз бұрын көргенбіз; Аполлоний шеңберінің диаметрінің бір Р ұшы барлық уақытта А және В нүктелерінің арасында, ал екінші Q ұшы АВ кесіндісінен тыс жататын болғандықтан, бұл шеңберлер қашан да АВ түзуіне қарағанда симметриялы екі Е және Е₁ нүктелерінде қиылысады (Е₁ нүктесі суретте белгіленбеген); сондықтан АВЕ мен АВЕ₁ үшбұрыштары тең болады. Егер В нүктесін алғашқы нүкте ретінде алсақ (ВЕ: АЕ = m: п), онда АВЕ мен АВЕ₁ үшбұрыштарына тең тағы да екі үшбұрыш шығады, яғни есептің бір шешімі болады.

Н ұ с қ а у. Катеттерінің m:n қатынасы мен 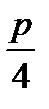гипотенузасы бойынша тікбұрышты АВС үшбұрышын салып, бұл есепті гомотетия әдісімен де шешуге болады.